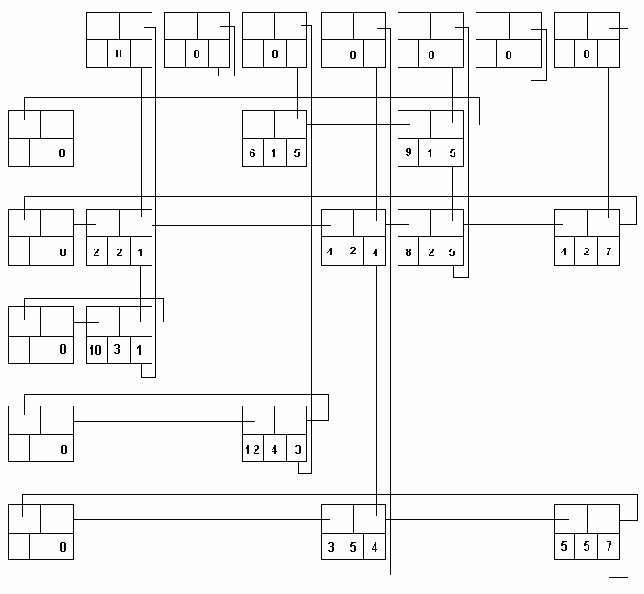
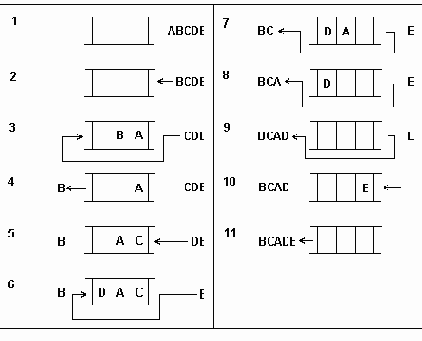
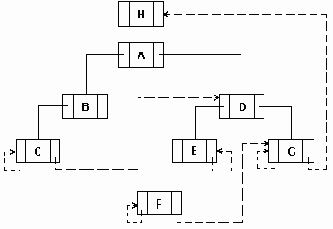
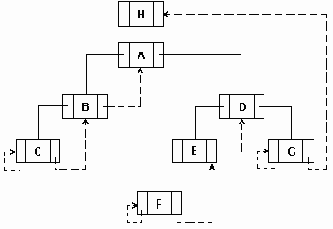
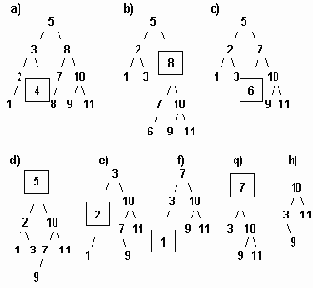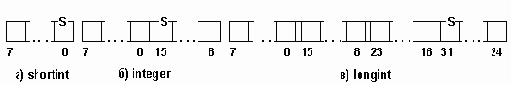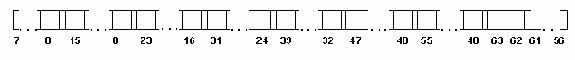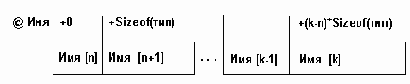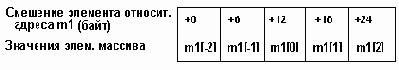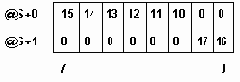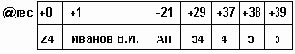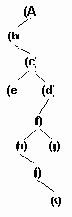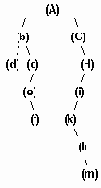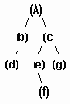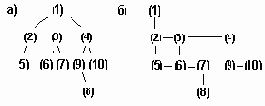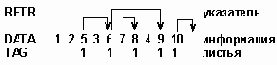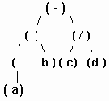а..h удаление узлов из сбалансированого дерева.
Рисунок6.36 а..h Удаление узлов из сбалансированого дерева.
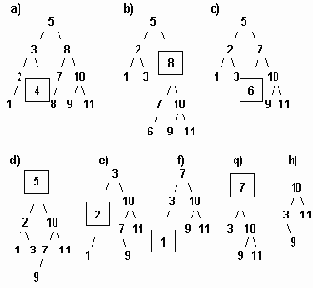
Удаление элемента из сбалансированного дерева удобнее разбить на 4 отдельных процедуры:
1. Delete - осуществляет рекурсивный поиск по дереву удаляемого элемента, вызывает процедуры удаления и балансировки. 2. Del - осуществляет собственно удаление элемента и вызов при необходимости процедуры балансировки. 3. Balance_L и Balance_R - производят балансировку и коррекцию показателей сбалансированности после удаления элемента из левого (правого) поддерева.
Классификация структур данных
Рисунок 1.1. Классификация структур данных
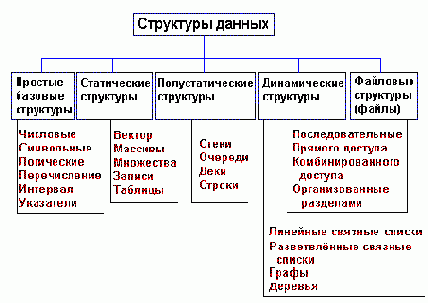
Важный признак структуры данных - характер упорядоченности ее элементов. По этому признаку структуры можно делить на ЛИНЕЙНЫЕ И НЕЛИНЕЙНЫЕ структуры.
В зависимости от характера взаимного расположения элементов в памяти линейные структуры можно разделить на структуры с ПОСЛЕДОВАТЕЛЬНЫМ распределением элементов в памяти (векторы, строки, массивы, стеки, очереди) и структуры с ПРОИЗВОЛЬНЫМ СВЯЗНЫМ распределением элементов в памяти ( односвязные, двусвязные списки). Пример нелинейных структур - многосвязные списки, деревья, графы.
В языках программирования понятие "структуры данных" тесно связано с понятием "типы данных". Любые данные, т.е. константы, переменные, значения функций или выражения, характеризуются своими типами.
Информация по каждому типу однозначно определяет :
1) структуру хранения данных указанного типа, т.е. выделение памяти и представление данных в ней, с одной стороны, и интерпретирование двоичного представления, с другой; 2) множество допустимых значений, которые может иметь тот или иной объект описываемого типа; 3) множество допустимых операций, которые применимы к объекту описываемого типа.
В последующих главах данного пособия рассматриваются структуры данных и соответствующие им типы данных. При описании базовых (простых) типов и при конструировании сложных типов мы ориентировались в основном на язык PASCAL. Этот язык использовался и во всех иллюстративных примерах. PASCAL был создан Н.Виртом специально для иллюстрирования структур данных и алгоритмов и традиционно используется для этих целей. Читатель знакомый с любым другим процедурным языком программирования общего назначения (C, FORTRAN, ALGOL, PL/1 и т.д.), без труда найдет аналогичные средства в известном ему языке.
Рисунок 1.1. Классификация структур данных

Важный признак структуры данных - характер упорядоченности ее элементов. По этому признаку структуры можно делить на ЛИНЕЙНЫЕ И НЕЛИНЕЙНЫЕ структуры.
В зависимости от характера взаимного расположения элементов в памяти линейные структуры можно разделить на структуры с ПОСЛЕДОВАТЕЛЬНЫМ распределением элементов в памяти (векторы, строки, массивы, стеки, очереди) и структуры с ПРОИЗВОЛЬНЫМ СВЯЗНЫМ распределением элементов в памяти ( односвязные, двусвязные списки). Пример нелинейных структур - многосвязные списки, деревья, графы.
В языках программирования понятие "структуры данных" тесно связано с понятием "типы данных". Любые данные, т.е. константы, переменные, значения функций или выражения, характеризуются своими типами.
Информация по каждому типу однозначно определяет :
1) структуру хранения данных указанного типа, т.е. выделение памяти и представление данных в ней, с одной стороны, и интерпретирование двоичного представления, с другой; 2) множество допустимых значений, которые может иметь тот или иной объект описываемого типа; 3) множество допустимых операций, которые применимы к объекту описываемого типа.
В последующих главах данного пособия рассматриваются структуры данных и соответствующие им типы данных. При описании базовых (простых) типов и при конструировании сложных типов мы ориентировались в основном на язык PASCAL. Этот язык использовался и во всех иллюстративных примерах. PASCAL был создан Н.Виртом специально для иллюстрирования структур данных и алгоритмов и традиционно используется для этих целей. Читатель знакомый с любым другим процедурным языком программирования общего назначения (C, FORTRAN, ALGOL, PL/1 и т.д.), без труда найдет аналогичные средства в известном ему языке.
Структура простых типов pascal.
Рисунок 2.1. Структура простых типов PASCAL.
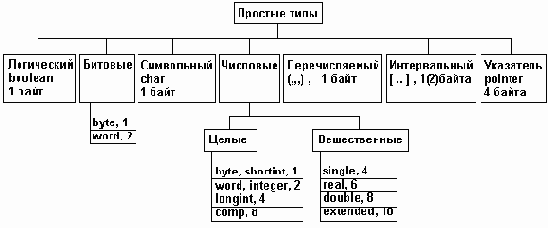
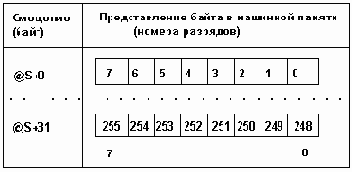
Формат представления вещественных чисел
Рисунок 2.5. Формат представления вещественных чисел

Однако, чаще вместо порядка используется характеристика, получающаяся прибавлением к порядку такого смещения, чтобы характеристика была всегда положительный. При этом имеет место формат представления вещественных чисел такой, как на рис 2.5 б).
Введение характеристики избавляет от необходимости выделять один бит для знака порядка и упрощает выполнение операций сравнения (,=) и арифметических операций над вещественными числами. Так, при сложении или вычитании чисел с плавающей точкой для того, чтобы выровнять операнды, требуется сдвиг влево или вправо мантиссы числа. Сдвиг можно осуществить с помощью единственного счетчика, в который сначала заносится положительное чис- ло, уменьшающееся затем до тех пор, пока не будет выполнено требуемое число сдвигов.
Таким образом, для представления вещественных чисел в памяти ЭВМ порядок p вещественного числа представляется в виде характеристики путем добавления смещения (старшего бита порядка):
Х = 2^(n-1) + k + p, (2.1)
где:
n - число бит, отведенных для характеристики, p - порядок числа, k - поправочный коэффициент фирмы IBM, равный +1 для real и -1 для форматов single, double, extended.
Формулы для вычисления характеристики и количество бит, необходимых для ее хранения, приведены в таблице 2.2.
Sizeof(тип)-размер слота (количество байтов памяти для записи одного элемента вектора), (k-n)*Sizeof(тип) - относительный адрес элемента с номером k, или, что тоже самое, смещение элемента с номером k.
Например: var m1:array[-2..2] of real;
представление данного вектора в памяти будет как на рис. 3.2.
В языках, где память распределяется до выполнения программы на этапе компиляции (C, PASCAL, FORTRAN), при описании типа вектора граничные значения индексов должны определены. В языках, где память может распределяться динамически (ALGOL, PL/1), значения индексов могут быть заданы во время выполнения программы.
Количество байтов непрерывной области памяти, занятых одновременно вектором, определяется по формуле:
ByteSise = ( k - n + 1 ) * Sizeof (тип)
Обращение к i-тому элементу вектора выполняется по адресу вектора плюс смещение к данному элементу. Смещение i-ого элемента вектора определяется по формуле:
ByteNumer = ( i- n ) * Sizeof (тип), а адрес его: @ ByteNumber = @ имя + ByteNumber.
где @ имя - адрес первого элемента вектора.
Например: var МAS: array [ 5..10 ] of word.
Базовый тип элемента вектора - Word требует 2 байта, поэтому на каждый элемент вектора выделяется по два байта. Тогда таблица 3.1 смещений элементов вектора относительно @Mas выглядит так:
Многомерные массивы хранятся в непрерывной области памяти. Размер слота определяется базовым типом элемента массива. Количество элементов массива и размер слота определяют размер памяти для хранения массива. Принцип распределения элементов массива в памяти определен языком программирования. Так в FORTRAN элементы распределяются по столбцам - так, что быстрее меняется левые индексы, в PASCAL - по строкам - изменение индексов выполняется в направлении справа налево.
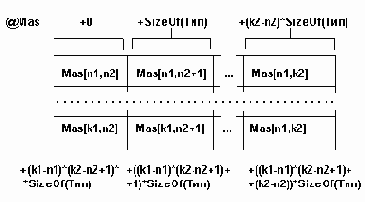
Адресом массива является адрес первого байта начального компонента массива. Смещение к элементу массива Mas[i1,i2] определяется по формуле:
ByteNumber = [(i1-n1)*(k2-n2+1)+(i2-n2)]*SizeOf(Тип) его адрес : @ByteNumber = @mas + ByteNumber. Например: var Mas : Array [3..5] [7..8] of Word;
Базовый тип элемента Word требует два байта памяти, тогда таблица 3.2 смещений элементов массива относительно @Mas будет следующей:
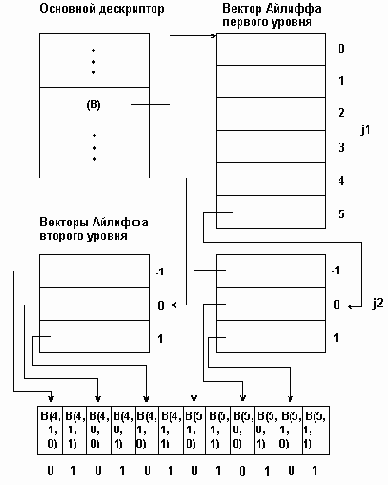
Для массива любой мерности формируется набор дескрипторов: основного и несколько уровней вспомогательных дескрипторов, называемых векторами Айлиффа. Каждый вектор Айлиффа определЯнного уровня содержит указатель на нулевые компоненты векторов Айлиффа следующего, более низкого уровня, а векторы Айлиффа самого нижнего уровня содержат указатели групп элементов отображаемого масси- ва. Основной дескриптор массива хранит указатель вектора Айлиффа первого уровня. При такой организации к произвольному элементу В(j1,j2,...,jn) многомерного массива можно обратиться пройдя по цепочке от основного дескриптора через соответствующие компоненты векторов Айлиффа.
На рис. 3.4 приведена физическая структура трЯхмерного массива В[4..5,-1..1,0..1], представленная по методу Айлиффа. Из этого рисунка видно, что метод Айлиффа, увеличивая скорость доступа к элементам массива, приводит в то же время к увеличению суммарного объЯма памяти, требуемого для представления массива. В этом заключается основной недостаток представления массивов с по- мощью векторов Айлиффа.
Представление в памяти переменной типа record в виде последовательности полей
Рисунок 3.10. Представление в памяти переменной типа record в виде последовательности полей
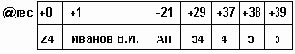
б) в виде связного списка с указателями на значения полей записи. При такой организации имеет место быстрое обращение к элементам, но очень неэкономичный расход памяти для хранения. Структура хранения в памяти связного списка с указателями на элементы приведена на рис. 3.11.
Представление в памяти переменной типа record в виде связного списка.
Рисунок 3.11. Представление в памяти переменной типа record в виде связного списка.
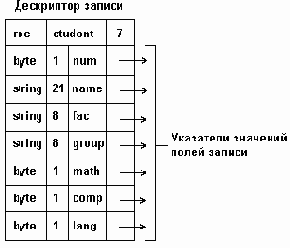
Примечание: для экономии объема памяти, отводимой под запись, значения некоторых ее полей хранятся в самом дескрипторе, вместо указателей, тогда в дескрипторе должны быть записаны соответствующие признаки.
В соответствии с общим подходом языка C дескриптор записи (в этом языке записи называются структурами) не сохраняется до выполнения программы. Поля структуры просто располагаются в смежных слотах памяти, обращения к отдельным полям заменяются на их адреса еще на этапе компиляции.
Полем записи может быть в свою очередь интегрированная структура данных - вектор, массив или другая запись. В некоторых языках программирования (COBOL, PL/1) при описании вложенных записей указывается уровень вложенности, в других (PASCAL, C) - уровень вложенности определяется автоматически.
Полем записи может быть другая запись,но ни в коем случае не такая же. Это связано прежде всего с тем, что компилятор должен выделить для размещения записи память. Предположим, описана запись вида:
type rec = record f1 : integer; f2 : char[2]; f3 : rec; end;
Как компилятор будет выделять память для такой записи? Для поля f1 будет выделено 2 байта, для поля f2 - 2 байта, а поле f3 - запись, которая в свою очередь состоит из f1 (2 байта), f2 (2 байта) и f3, которое... и т.д. Недаром компилятор C, встретив подобное описание, выдает сообщение о нехватке памяти.
Однако, полем записи вполне может быть указатель на другую такую же запись: размер памяти, занимаемой указателем известен и проблем с выделением памяти не возникает. Этот прием широко используется в программировании для установления связей между однотипными записями (см. главу 5).
Представление строк векторами постоянной длины
Рисунок 4.3. Представление строк векторами постоянной длины

Представление строк переменной длины с признаком конца
Рисунок 4.4. Представление строк переменной длины с признаком конца

Представление строки многосимвольными звеньями постоянной длины
Рисунок 4.9. Представление строки многосимвольными звеньями постоянной длины
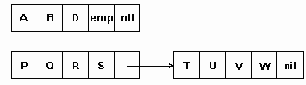
Такое представление обеспечивает более эффективное использование памяти, чем символьно-связное. Операции вставки/удаления в ряде случаев могут сводиться к вставке/удалению целых блоков. Однако, при удалении одиночных символов в блоках могут накапливаться пустые символы emp, что может привести даже к худшему использованию памяти, чем в символьно-связном представлении.
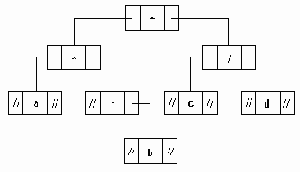
Структура элемента разветвленного списка
Рисунок 5.16. Структура элемента разветвленного списка

В этом случае указатель down указывает на данные или на подсписок. Поскольку списки могут составляться из данных различных типов, целесообразно адресовать указателем down не непосредственно данные, а их дескриптор, в котором может быть описан тип данных, их длина и т.п. Само описание того, является ли адресуемый указателем данных объект атомом или узлом также может находиться в этом дескрипторе. Удобно сделать размер дескриптора данных таким же, как и элемента списка. В этом случае размер поля type может быть расширен, например, до 1 байта и это поле может индицировать не только атом/подсписок, но и тип атомарных данных, поле next в дескрипторе данных может использоваться для представления еще какой-то описательной информации, например, размера атома. На рис.5.17 показано представление элементами такого формата списка: (КОВАЛЬ,(12,7,53),d). Первая (верхняя) строка на рисунке представляет элементы списка, вторая - элементы подсписка, третья - дескрипторы данных, четвертая - сами данные. В поле type каждого элемента мы использовали коды: n - узел, S - атом, тип STRING, I - атом, тип INTEGER, C - атом, тип CHAR.
Изображения бинарных деревьев
Рисунок 6.13. Изображения бинарных деревьев
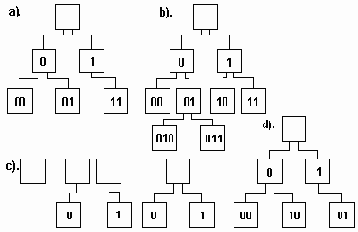
Бинарные деревья, изображенные на рис.6.13(a) и 6.13(d), представляют собой разные позиционные деревья, хотя они не являются разными упорядоченными деревьями.
В позиционном бинарном дереве каждая вершина представлена единственным образом посредством строки символов над алфавитом {0,1}, при этом корень характеризуется пустой строкой. Любой сын вершины "u" характеризуется строкой, префикс (начальная часть) которой является строкой, характеризующей "u".
Примером бинарного дерева является фамильное дерево с отцом и матерью человека в качестве его потомков. Еще один пример - это арифметическое выражение с двухместными операциями, где каждая операция представляет собой ветвящийся узел с операндами в качестве поддеревьев.
Представить m-арное дерево в памяти ЭВМ сложно, т.к. каждый элемент дерева должен содержать столько указателей, сколько ребер выходит из узла (при m-3,4.5.6... соответствует 3,4,5,6... указателей). Это приведет к повышенному расходу памяти ЭВМ, разнообразию исходных элементов и усложнит алгоритмы обработки дерева. Поэтому m-арные деревья, лес необходимо привести к бинарным для экономии памяти и упрощению алгоритмов. Все узлы бинарного дерева представляются в памяти ЭВМ однотипными элементами с двумя указателями (см.разд. 6,2,5), кроме того, операции над двоичными деревьями выполняются просто и эффективно.
Логическое представление дерева
Рисунок 6.20. Логическое представление дерева
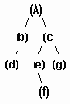
Машинное связное представление дерева представленного
Рисунок 6.21. Машинное связное представление дерева представленного на рис.6.20
Рассмотрим последовательное представление деревьев. Оно удобно и эффективно в случае, если древовидная структура в течение времени своего существования не подвергается значительным изменениям, за счет включения вершин, удаления вершин и т.д.
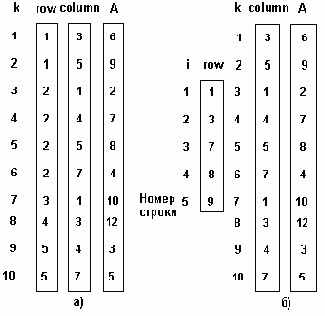
Выбор метода последовательного представления деревьев определяется также набором тех операций, которые должны быть выполнены над древовидными структурами. (Пример статистической древовидной структуры - пирамидальный метод сортировки). Простейший метод представления дерева в виде последовательной структуры заключается во введении вектора FATHER, задающего отбор для всех его вершин. Этот метод можно использовать также для представления леса. Недостаток метода - он не отображает упорядочения вершин дерева. Если в предыдущем примере поменять местами вершины 9 и 10, последовательное представление останется тем же.
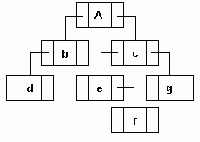
Диаграммы дерева: а) исходное б) перестройка в бинарное
Рисунок 6.22. Диаграммы дерева: а) исходное б) перестройка в бинарное
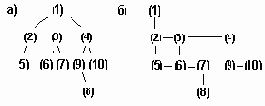
Последовательное представление дерева, логическая диаграмма которого дана на рис. 6.22 , задается следующим образом:
i 1 2 3 4 5 6 7 8 9 10 FATHER [i] 0 1 1 1 2 3 3 7 4 4 ,
где ветви определяются как {(FATHER[i],i)}, i = 2,3,...,10.
Вершины 2,3,4 являются сыновьями вершины 1, вершина 5 - сыном вершины 2, вершины 6,7 - сыновьями вершины 3, вершина 8 имеет отца вершина 7 и вершины 9 и 10 - сыновья вершины 4.
Числовые поля данных используются здесь, чтобы упростить представление дерева. Корневая вершина не имеет отца, поэтому вместо отца для нее задается нулевое значение.
Общее правило: если T обозначает индекс корневой вершины дерева, то FATHER[T] = 0.
Другой метод последовательного представления деревьев заключается в использовании физической смежности элементов машинной памяти вместо одного из полей LPTR или RPTR, например, способ опускания полей, т.е. чтобы вершины появлялись в нисходящем порядке. Дерево (рис.6.22б), можно описать как:
Последовательное представление дерева методом опускания полей
Рисунок 6.23. Последовательное представление дерева методом опускания полей
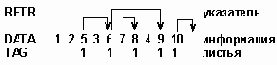
где RPTR,DATA и TAG представляют векторы. В данном методе указатель LPTR не требуется, т.к. если бы он не был пуст, то указывал бы на вершину, стоящую непосредственно справа от данной. Вектор TAG - бинарный вектор, в котором единицы отмечают концевые вершины исходного дерева. При таком представлении имеются значительные потери памяти, т.к. свыше половины указателей RPTR оказываются пустыми. Эти пустые места можно использовать путем установки указателя RPTR каждой данной вершины на вершину, которая следует непосредственно за поддеревом, расположенном под ней. В таком представлении поле RPTR переименовывается в RANGE:
Последовательное представление дерева с размещением вершин в возрастающем порядке
Рисунок 6.24. Последовательное представление дерева с размещением вершин в возрастающем порядке
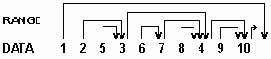
В этом случае поле TAG не требуется поскольку концевой узел определяется условием RANGE(P) = P + 1.
Третий метод состоит в представлении дерева общего вида на основе его восходящего обхода. Такое представление состоит из двух векторов: один вектор описывает все вершины дерева в восходящей последовательности, а второй - задает полустепени исхода этих вершин (см. рис.6.25). Восходящий метод представления удобен для вычисления функцией, заданных на определенных вершинах дерева ( например, использование таких функций для генерации объектного кода по обратной польской записи некоторого выражения ).
Последовательное представление дерева на основе восходящего обхода
Рисунок 6.25. Последовательное представление дерева на основе восходящего обхода
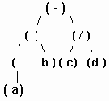
В заключении приведем два важных понятия.
Подобие бинарных деревьев - два дерева подобны, если они имеют одинаковую структуру ( форму ).
Эквивалентные бинарные деревья - два дерева эквивалентные, если они подобны, и если соответствующие вершины у них содержат одинаковую информацию.
Трассировка смешанного обхода с прошивкой приведена в табл.6.4.
перемножать, вычитать, дифференцировать, интегрировать, сравнивать на эквивалентность и т.д. Т.е. получаются символьные выражения, которые можно закодировать в виде таблиц:
(-) - операция унарного минуса; () - операция возведения в степень; (+) - операция сложения; (*) - операция умножения; (/) - операция деления. (Е) - указательная переменная, адресующая корень дерева, каждая вершина которого состоит из левого указателя (LPТR), правого указателя (RPTR) и информационного поля TYPE.
Для неконцевой вершины поле TYPE задает арифметическую операцию, связанную с этой вершиной. Значения поля TYPE вершин +,-,*, /, (-) и равны 1, 2, 3, 4, 5, 6 соответственно.
Для концевых вершин поле символа в TYPE имеет значение 0, что означает константу или переменную. В этом случае правый указатель вершины задает адрес таблицы символов, который соответствует данной константе или переменной. В дереве указывается тип оператора, а не он сам, что позволяет упростить обработку таких деревьев.
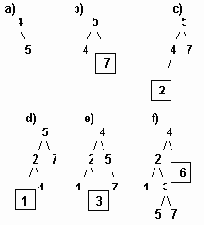
последовательное включение узлов в сбалансированное дерево.
Рисунок 6.35 Последовательное включение узлов в сбалансированное дерево.
Симметричные массивы.
Симметричные массивы.
Двумерный массив, в котором количество строк равно количеству столбцов называется квадратной матрицей. Квадратная матрица, у которой элементы, расположенные симметрично относительно главной диагонали, попарно равны друг другу, называется симметричной. Если матрица порядка n симметрична, то в ее физической структуре достаточно отобразить не n^2, а лишь n*(n+1)/2 еЯ элементов. Иными словами, в памяти необходимо представить только верхний (включая и диагональ) треугольник квадратной логической структуры. Доступ к треугольному массиву организуется таким образом, чтобы можно было обращаться к любому элементу исходной логической структуры, в том числе и к элементам, значения которых хотя и не представлены в памяти, но могут быть определены на основе значений симметричных им элементов.
На практике для работы с симметричной матрицей разрабатываются процедуры для:
а) преобразования индексов матрицы в индекс вектора,
б) формирования вектора и записи в него элементов верхнего треугольника элементов исходной матрицы,
в) получения значения элемента матрицы из ее упакованного представления. При таком подходе обращение к элементам исходной матрицы выполняется опосредованно, через указанные функции.
В приложении приведен пример программы для работы с симметричной матрицей.
Символьно - связное представление строк.
СИМВОЛЬНО - СВЯЗНОЕ ПРЕДСТАВЛЕНИЕ СТРОК.
Списковое представление строк в памяти обеспечивает гибкость в выполнении разнообразных операций над строками (в частности, операций включения и исключения отдельных символов и целых цепочек) и использование системных средств управления памятью при выделении необходимого объема памяти для строки. Однако, при этом возникают дополнительные расходы памяти. Другим недостатком спискового представления строки является то, что логически соседние элементы строки не являются физически соседними в памяти. Это усложняет доступ к группам элементов строки по сравнению с доступом в векторном представлении строки.
Слияние двух списков.
Слияние двух списков.
Операция слияния заключается в формировании из двух списков одного - она аналогична операции сцепления строк. В случае односвязного списка, показанном в примере 5.7, слияние выполняется очень просто. Последний элемент первого списка содержит пустой указатель на следующий элемент, этот указатель служит признаком конца списка. Вместо этого пустого указатель в последний элемент первого списка заносится указатель на начало второго списка. Таким образом, второй список становится продолжением первого.
{==== Программный пример 5.7 ====} { Слияние двух списков. head1 и head2 - указатели на начала списков. На результирующий список указывает head1 } Procedure Unite (var head1, head2 : sllptr); var cur : sllptr; begin { если 2-й список пустой - нечего делать } if head2<>nil then begin { если 1-й список пустой, выходным списком будет 2-й } if head1=nil then head1:=head2 else { перебор 1-го списка до последнего его эл-та } begin cur:=head1; while cur^.next<>nil do cur:=cur^.next; { последний эл-т 1-го списка указывает на начало 2-го } cur^.next:=head2; end; head2:=nil; { 2-й список аннулируется } end; end;
Сортировка частично упорядоченным деревом.
Сортировка частично упорядоченным деревом.
В двоичном дереве, которое строится в этом методе сортировки для каждого узла справедливо следующее утверждение: значения ключа, записанное в узле, меньше, чем ключи его потомков. Для полностью упорядоченного дерева имеются требования к соотношению между ключами потомков. Для данного дерева таких требований нет, поэтому такое дерево и называется частично упорядоченным. Кроме того, наше дерево должно быть абсолютно сбалансированным. Это означает не только то, что длины путей к любым двум листьям различаются не более, чем на 1, но и то, что при добавлении нового элемента в дерево предпочтение всегда отдается левой ветви/подветви, пока это не нарушает сбалансированность. Более подробно деревья рассматриваются в гл.6.
Например, последовательность чисел:
3 20 12 58 35 30 32 28
будет представлена в виде дерева, показанного на рис.3.15 .
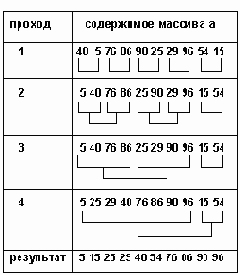
Сортировка попарным слиянием.
Сортировка попарным слиянием.
Входное множество рассматривается, как последовательность подмножеств, каждое из которых состоит из единственного элемента и, следовательно, является уже упорядоченным. На первом проходе каждые два соседних одно-элементных множества сливаются в одно двух-элементное упорядоченное множество. На втором проходе двух-элементные множества сливаются в 4-элементные упорядоченные множества и т.д. В конце концов мы получаем одно большое упорядоченное множество.
Важнейшей частью алгоритма является слияние двух упорядоченных множеств. Эту часть алгоритма мы опишем строго.
1. [Начальные установки]. Определить длины первого и второго исходных множеств - l1 и l2 соответственно. Установить индексы текущих элементов в исходных множествах i1 и i2 в 1. Установить индекс в выходном множестве j=1. 2. [Цикл слияния]. Выполнять шаг 3 до тех пор, пока i13. [Сравнение]. Сравнить ключ i1-го элемента из 1-го исходного множества с ключом i2-го элемента из второго исходного множества. Если ключ элемента из 1-го множества меньше, то записать i1-ый элемент из 1-го множества на j-ое место в выходное множество и увеличить i1 на 1. Иначе - записать i2-ой элемент из 2-го множества на j-ое место в выходное множество и увеличить i2 на 1. Увеличить j на 1. 4. [Вывод остатка]. Если i1
Программный пример 3.17 иллюстрирует сортировку попарным слиянием в ее обменном варианте - выходные множества формируются на месте входных.
{===== Программный пример 3.17 =====} { Сортировка слиянием } Procedure Sort(var a :Seq); Var i0,j0,i,j,si,sj,k,ke,t,m : integer; begin si:=1; { начальный размер одного множества } while si < N do begin { цикл пока одно множество не составит весь массив } i0:=1; { нач. индекс 1-го множества пары } while i0 < N do begin { цикл пока не пересмотрим весь массив } j0:=i0+si; { нач. индекс 2-го множества пары } i:=i0; j:=j0; { размер 2-го множества пары может ограничиваться концом массива } if si > N-j0+1 then sj:=N-j0+1 else sj:=si; if sj > 0 then begin k:=i0; { нач. индекс слитого множества } while (i < i0+si+sj) and (j a[j] then begin { если эл-т 1-го a[j] } k:=k+1; { вых. множество увеличилось } i:=i+1; { если был перенос - за счет сдвига, если не было - за счет перехода эл-та в вых. } end; { while } end; { if sj > 0 } i0:=i0+si*2; { начало следующей пары } end; { while i0 < N } si:=si*2; { размер эл-тов пары увеличивается вдвое } end; { while si < N } end;
Результаты трассировки примера приведены в таблице 3.11. Для каждого прохода показаны множества, которые на этом проходе сливаются. Обратите внимание на обработку последнего множества, оставшегося без пары.
Сортировка простой выборкой.
Сортировка простой выборкой.
Данный метод реализует практически "дословно" сформулированную выше стратегию выборки. Порядок алгоритма простой выборки - O(N^2). Количество пересылок - N.
Алгоритм сортировки простой выборкой иллюстрируется программным примером 3.7.
В программной реализации алгоритма возникает проблема значения ключа "пусто". Довольно часто программисты используют в качестве такового некоторое заведомо отсутствующее во входной последовательности значение ключа, например, максимальное из теоретически возможных значений. Другой, более строгий подход - создание отдельного вектора, каждый элемент которого имеет логический тип и отражает состояние соответствующего элемента входного множества ("истина" - "непусто", "ложь" - "пусто"). Именно такой подход реализован в нашем программном примере. Роль входной последовательности здесь выполняет параметр a, роль выходной - параметр b, роль вектора состояний - массив c. Алгоритм несколько усложняется за счет того, что для установки начального значения при поиске минимума приходится отбрасывать уже "пустые" элементы.
{===== Программный пример 3.7 =====} Procedure Sort( a : SEQ; var b : SEQ); Var i, j, m : integer; c: array[1..N] of boolean; {состояние эл-тов вх.множества} begin for i:=1 to N do c[i]:=true; { сброс отметок} for i:=1 to N do {поиск 1-го невыбранного эл. во вх.множестве} begin j:=1; while not c[j] do j:=j+1; m:=j; { поиск минимального элемент а} for j:=2 to N do if c[j] and (a[j] < a[m]) then m:=j; b[i]:=a[m]; { запись в выходное множество} c[m]:=false; { во входное множество - "пусто" } end; end;
Сортировка простыми вставками.
Сортировка простыми вставками.
Этот метод - "дословная" реализации стратегии включения. Порядок алгоритма сортировки простыми вставками - O(N^2), если учитывать только операции сравнения. Но сортировка требует еще и в среднем N^2/4 перемещений, что де- лает ее в таком варианте значительно менее эффективной, чем сортировка выборкой.
Алгоритм сортировки простыми вставками иллюстрируется программным примером 3.11.
{===== Программный пример 3.11 =====} Procedure Sort(a : Seq; var b : Seq); Var i, j, k : integer; begin for i:=1 to N do begin { перебор входного массива } { поиск места для a[i] в выходном массиве } j:=1; while (j < i) and (b[j]
Эффективность алгоритма может быть несколько улучшена при применении не линейного, а дихотомического поиска. Однако, следует иметь в виду, что такое увеличение эффективности может быть достигнуто лишь на множествах значительного по количеству элементов объема. Т.к. алгоритм требует большого числа пересылок, при значительном объеме одной записи эффективность может определяться не количеством операций сравнения, а количеством пересылок.
Реализация алгоритма обменной сортировки простыми вставками отличается от базового алгоритма только тем, что входное и выходное множество разделяют одну область памяти.
Сортировка шелла.
Сортировка Шелла.
Это еще одна модификация пузырьковой сортировки. Суть ее состоит в том, что здесь выполняется сравнение ключей, отстоящих один от другого на некотором расстоянии d. Исходный размер d обычно выбирается соизмеримым с половиной общего размера сортируемой последовательности. Выполняется пузырьковая сортировка с интервалом сравнения d. Затем величина d уменьшается вдвое и вновь выполняется пузырьковая сортировка, далее d уменьшается еще вдвое и т.д. Последняя пузырьковая сортировка выполняется при d=1. Качественный порядок сортировки Шелла остается O(N^2), среднее же число сравнений, определенное эмпирическим путем - log2(N)^2*N. Ускорение достигается за счет того, что выяв- ленные "не на месте" элементы при d>1, быстрее "всплывают" на свои места.
Пример 3.10 иллюстрирует сортировку Шелла.
{===== Программный пример 3.10 =====} Procedure Sort( var a : seq); Var d, i, t : integer; k : boolean; { признак перестановки } begin d:=N div 2; { начальное значение интервала } while d > 0 do { цикл с уменьшением интервала до 1 } begin k:=true; {пузырьковая сортировка с интервалом d} while k do { цикл, пока есть перестановки } begin k:=false; i:=1; for i:=1 to N-d do { сравнение эл-тов на интервале d } begin if a[i] > a[i+d] then begin t:=a[i]; a[i]:=a[i+d]; a[i+d]:=t; { перестановка } k:=true; { признак перестановки } end; { if ... } end; { for ... } end; { while k } d:=d div 2; { уменьшение интервала } end; { while d>0 } end;
Результаты трассировки программного примера 3.10 представлены в таблице 3.7.
Алгоритм складывается из построения упорядоченного двоичного дерева и последующего его обхода. Если нет необходимости в построении всего линейного упорядоченного списка значений, то нет необходимости и в обходе дерева, в этом случае применяется поиск в упорядоченном двоичном дереве. Алгоритмы работы с упорядоченными двоичными деревьями подробно рассмотрены в главе 6. Отметим, что порядок алгоритма - O(N*log2(N)), но в конкретных случаях все зависит от упорядоченности исходной последовательности, который влияет на степень сбалансированности дерева и в конечном счете - на эффективность поиска.
Орграф представляется связным нелинейным списком, если он часто изменяется или если полустепени захода и исхода его узлов велики. Рассмотрим два варианты представления орграфов связными нелинейными списковыми структурами.
В первом варианте два типа элементов - атомарный и узел связи (см. раздел 5.5). На рис.6.5 показана схема такого представления для графа рис.6.2. Скобочная запись связей этого графа:
( < A,B >, < B,C >, < C,D >, < B,D >, < D,C > )
что обменный вариант обеспечивает экономию
Таблица 3.5
Очевидно, что обменный вариант обеспечивает экономию памяти. Очевидно также, что здесь не возникает проблемы "пустого" значения. Общее число сравнений уменьшается вдвое - N*(N-1)/2, но порядок алгоритма остается степенным - O(n^2). Количество перестановок N-1, но перестановка, по-видимому, вдвое более времяемкая операция, чем пересылка в предыдущем алгоритме.
Довольно простая модификация обменной сортировки выборкой предусматривает поиск в одном цикле просмотра входного множества сразу и минимума, и максимума и обмен их с первым и с последним элементами множества соответственно. Хотя итоговое количество сравнений и пересылок в этой модификации не уменьшается, достигается экономия на количестве итераций внешнего цикла.
Приведенные выше алгоритмы сортировки выборкой практически нечувствительны к исходной упорядоченности. В любом случае поиск минимума требует полного просмотра входного множества. В обменном варианте исходная упорядоченность может дать некоторую экономию на перестановках для случаев, когда минимальный элемент найден на первом месте во входном множестве.
Еще одна модификация пузырьковой сортировки
Таблица 3.6
Еще одна модификация пузырьковой сортировки носит название шейкер-сортировки. Суть ее состоит в том, что направления просмотров чередуются: за просмотром от начала к концу следует просмотр от конца к началу входного множества. При просмотре в прямом направлении запись с самым большим ключом ставится на свое место в последовательности, при просмотре в обратном направлении - запись с самым маленьким. Этот алгоритм весьма эффективен для задач восстановления упорядоченности, когда исходная последовательность уже была упорядочена, но подверглась не очень значительным изменениям. Упорядоченность в последовательности с одиночным изменением будет гарантированно восстановлена всего за два прохода.
Хотя обменные алгоритмы стратегии включения
Таблица 3.8
Хотя обменные алгоритмы стратегии включения и позволяют сократить число сравнений при наличии некоторой исходной упорядоченности входного множества, значительное число пересылок существенно снижает эффективность этих алгоритмов. Поэтому алгоритмы включения целесообразно применять к связным структурам данных, когда операция перестановки элементов структуры требует не пересылки данных в памяти, а выполняется способом коррекции указателей (см. главу 5).
Еще одна группа включающих алгоритмов сортировки использует структуру дерева. Мы рекомендуем читателю повторно вернуться к рассмотрению этих алгоритмов после ознакомления с главой 6.
a name=
Таблица 3.11
< a name= lb4>
Таблица 6.1
Таблица 6.1
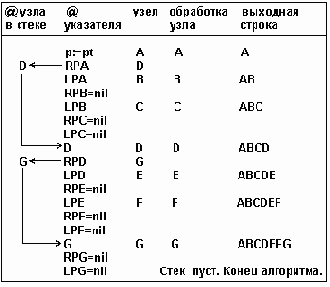
Рекурсивный смешанный обход описывается следующим
Таблица 6.2
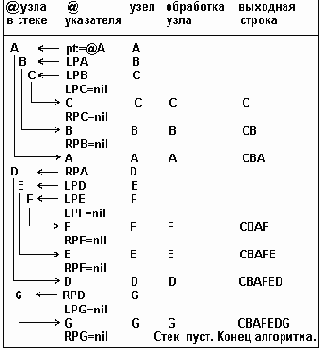
Рекурсивный смешанный обход описывается следующим образом:
1) Смешанный обход левого поддерева; 2) Обработка корневой вершины; 3) Смешанный обход правого поддерева.
Текст программы рекурсивной процедуры ( r_Inorder ) демонстрируется в программном примере 6.7.
{=== Программный пример 6.7. Рекурсивное выполнение смешанного обхода ===} Procedure r_Inorder(t: TreePtr); begin if t = nil then begin writeln('Дерево пусто'); exit; end; if t^.left <> nil then R_inorder (t^.left); (*--------------- Обработка данных звена --------------*) ................................ if t^.right <> nil then R_inorder(t^.right); End;
Текст процедуры добавления элемента.
ТЕКСТ ПРОЦЕДУРЫ ДОБАВЛЕНИЯ ЭЛЕМЕНТА.
Процедура создает новый элемент, заполняет его информационные поля и обнуляет указатели. При создании первого элемента он автоматически становится корнем дерева.
Procedure Create (x:integer; var p:ref; var h:boolean); { создание нового элемента } Begin NEW(p); h:=true; with p^ do begin key:=x; left:=nil; right:=nil; BAL:=0; end; if count=0 then root:=p; count:=count+1; End;
Текст процедуры insert_&_balanse.
ТЕКСТ ПРОЦЕДУРЫ Insert_&_Balanse.
Процедура выполняет действия по вставка элемента в бинарное дерево с последующей балансировкой в соответствии с приведенным выше алгоритмом.
{=====Программный пример 6.18=========} Procedure Insert_&_Balanse (x:integer; var p,root:ref; var h:boolean); { x=KEY, p=p, root=ROOT, h=h } var p1,p2:ref; {h=false} Begin if p=nil then Create(x,p,h) {слова нет в дереве,включить его} else if x=p^.key then begin gotoXY(35,3); write('Ключ найден!'); readln; exit; end; if x < p^.key then begin Insert_&_Balanse(x,p^.left,root,h); if h then {выросла левая ветвь} case p^.bal of 1: begin p^.bal:=0; h:=false; end; 0: p^.bal:=-1; -1: begin {балансировка} if p=root then root:=p^.left; p1:=p^.left; {смена указателя на вершину} if p1^.bal=-1 then begin {однократный LL-поворот} p^.left:=p1^.right; p1^.right:=p; p^.bal:=0; p:=p1; end else begin {2-кратный LR-поворот} if p1=root then root:=p1^.right; p2:=p1^.right; p1^.right:=p2^.left; p2^.left:=p1; p^.left:=p2^.right; p2^.right:=p; if p2^.bal=-1 then p^.bal:=+1 else p^.bal:=0; if p2^.bal=+1 then p1^.bal:=-1 else p1^.bal:=0; p:=p2; end; p^.bal:=0; h:=false; end; end;{case} end { h then} else if x > p^.key then begin Insert_&_Balanse(x,p^.right,root,h); if h then {выросла правая ветвь} case p^.bal of -1: begin p^.bal:=0; h:=false; end; 0: p^.bal:=+1; 1: begin {балансировка} if p=root then root:=p^.right; p1:=p^.right; {смена указателя на вершину} if p1^.BAL=+1 then begin {однократный RR-поворот} p^.right:=p1^.left; p1^.left:=p; p^.BAL:=0; p:=p1; end else begin {2-кратный RL-поворот} if p1=root then root:=p1^.left; p2:=p1^.left; p1^.left:=p2^.right; p2^.right:=p1; p^.right:=p2^.left; p2^.left:=p; if p2^.BAL=+1 then p^.BAL:=-1 else p^.BAL:=0; if p2^.BAL=-1 then p1^.BAL:=+1 else p1^.BAL:=0; p:=p2; end; p^.BAL:=0; h:=false; end; { begin 3 } end;{ case } end; {then } End {Search};
Текст процедуры search.
ТЕКСТ ПРОЦЕДУРЫ Search.
{=====Программный пример 6.21 ===========} Procedure Search (x:integer; var p:ref); begin if x > p^.key then if p=nil then writeln('Элемент на найден') else Search(x,p^.right); if x < p^.key then if p=nil then writeln('Элемент на найден') else Search(x,p^.left); writeln('элемент найден'); { Здесь - процедура обработки элемента } end;
Так как операция поиска применяется в процедуре вставки элемента в сбалансированное дерево, то нет особого смысла выделять эту операцию в отдельную процедуру. Проще предусмотреть, что при отсутствии элемента производится его включение, а если элемент уже есть - то производятся необходимые действия над элементом.
На первый взгляд работа со сбалансированными бинарными деревьями требует лишних затрат времени на дополнительные операции по поддержанию необходимой структуры дерева и усложнение алгоритмов.
Но на самом деле затраты на балансировку легко компенсируются минимальным временем поиска элементов при вставке, удалении и обработке элементов, по сравнению с другими методами хранения. В то же время четкая структура расположения элементов не усложняет, а наоборот - упрощает алгоритмы работы с такими деревьями.
Тип шаблона.
Тип шаблона.
В языке PL/1 тип шаблона описывается в программе, как: PICTURE '9...9'.
Это означает, что данное представляет собой целое число, содержащее столько цифр, сколько девяток указано в описании.
Турнирная сортировка.
Турнирная сортировка.
Этот метод сортировки получил свое название из-за сходства с кубковой системой проведения спортивных соревнований: участники соревнований разбиваются на пары, в которых разыгрывается первый тур; из победителей первого тура составляются пары для розыгрыша второго тура и т.д. Алгоритм сортировки состоит из двух этапов. На первом этапе строится дерево: аналогичное схеме розыгрыша кубка.
Например, для последовательности чисел a:
16 21 8 14 26 94 30 1
такое дерево будет иметь вид пирамиды, показанной на рис.3.13.
Вектор с управляемой длиной.
ВЕКТОР С УПРАВЛЯЕМОЙ ДЛИНОЙ.
Память под вектор с управляемой длиной отводится при создании строки и ее размер и размещение остаются неизменными все время существования строки. В дескрипторе такого вектора-строки может отсутствовать начальный индекс, так как он может быть зафиксирован раз навсегда установленными соглашениями, но появляется поле текущей длины строки. Размер строки, таким образом, может изменяться от 0 до значения максимального индекса вектора. "Лишняя" часть отводимой памяти может быть заполнена любыми кодами - она не принимается во внимание при оперировании со строкой. Поле конечного индекса может быть использовано для контроля превышения длиной строки объема отведенной памяти. Представление строк в виде вектора с управляемой длиной (при максимальной длине 10) показано на рис.4.6.
Хотя такое представление строк не обеспечивает экономии памяти, проектировщики систем программирования, как видно, считают это приемлемой платой за возможность работать с изменчивыми строками в статической памяти.
Векторное представление строк.
ВЕКТОРНОЕ ПРЕДСТАВЛЕНИЕ СТРОК.
Представление строк в виде векторов, принятое в большинстве универсальных языков программирования, позволяет работать со строками, размещенными в статической памяти. Кроме того, векторное представление позволяет легко обращаться к отдельным символам строки как к элементам вектора - по индексу.
Самым простым способом является представление строки в виде вектора постоянной длинны. При этом в памяти отводится фиксированное количество байт, в которые записываются символы строки. Если строка меньше отводимого под нее вектора, то лишние места заполняются пробелами, а если строка выходит за пределы вектора, то лишние (обычно справа строки) символы должны быть отброшены.
На рис.4.3 приведена схема, на которой показано представление двух строк: 'ABCD' и 'PQRSTUVW' в виде вектора постоянной длины на шесть символов.
Восходящий обход ( postorder, r_postorder ).
ВОСХОДЯЩИЙ ОБХОД ( Postorder, r_Postorder ).
Трудность заключается в том, что в отличие от Preorder в этом алгоритме каждая вершина запоминается в стеке дважды: первый раз - когда обходится левое поддерево, и второй раз - когда обходится правое поддерево. Таким образом, в алгоритме необходимо различать два вида стековых записей: 1-й означает, что в данный момент обходится левое поддерево; 2-й - что обходится правое, поэтому в стеке запоминается указатель на узел и признак (код-1 и код-2 соответственно).
Алгоритм восходящего обхода можно представить следующим образом:
1) Спуститься по левой ветви с запоминанием вершины в сте ке как 1-й вид стековых записей; 2) Если стек пуст, то перейти к п.5; 3) Выбрать вершину из стека, если это первый вид стековых записей, то возвратить его в стек как 2-й вид стековых запи сей; перейти к правому сыну; перейти к п.1, иначе перейти к п.4; 4) Обработать данные вершины и перейти к п.2; 5) Конец алгоритма.
Текст программы процедуры восходящего обхода ( Postorder) представлен в программном примере 6.8.
{=== Программный пример 6.8. Восходящий обход ====} Procedure Postorder (t: TreePtr); label 2; Var p: TreePtr; top: point; { стековый тип } Sign: byte; { sign=1 - первый вид стековых записей} { sign=2 - второй вид стековых записей} Begin (*------------- Инициализация ------------------*) if t = nil then begin writeln('Дерево пусто'); exit; end else begin p:=t; top:=nil; end; {инициализация стека} (*------- Запоминание адресов вдоль левой ветви -------*) 2: while p <> nil do begin s_Push(top,1,p); { заносится указатель 1-го вида} p:=p^.left; end; (*-- Подъем вверх по дереву с обработкой правых ветвей ----*) while top <> nil do begin p:=s_Pop(top,sign); if sign = 1 then begin s_Push(top,0,p); { заносится указатель 2-го вида } p:=p^.right; goto 2; end else (*---- Обработка данных звена ---------*) ................................ end; End; { Postorder }