Кластерный анализ

Основная цель Проверка статистической значимости Области применения Объединение (древовидная кластеризация) Иерархическое дерево Меры расстояния Правила объединения или связи Двувходовое объединение Вводный обзор Двувходовое объединение Метод K средних

Пример Вычисления Интерпретация результатов

Основная цель

Термин кластерный анализ (впервые ввел Tryon, 1939) в действительности включает в себя набор различных алгоритмов классификации. Общий вопрос, задаваемый исследователями во многих областях, состоит в том, как организовать наблюдаемые данные в наглядные структуры, т.е. развернуть таксономии. Например, биологи ставят цель разбить животных на различные виды, чтобы содержательно описать различия между ними. В соответствии с современной системой, принятой в биологии, человек принадлежит к приматам, млекопитающим, амниотам, позвоночным и животным. Заметьте, что в этой классификации, чем выше уровень агрегации, тем меньше сходства между членами в соответствующем классе. Человек имеет больше сходства с другими приматами (т.е. с обезьянами), чем с "отдаленными" членами семейства млекопитающих (например, собаками) и т.д. В последующих разделах будут рассмотрены общие методы кластерного анализа, см. Объединение (древовидная кластеризация), Двувходовое объединение и Метод K средних.

Проверка статистической значимости
Проверка статистической значимости

Заметим, что предыдущие рассуждения ссылаются на алгоритмы кластеризации, но ничего не упоминают о проверке статистической значимости. Фактически, кластерный анализ является не столько обычным статистическим методом, сколько "набором" различных алгоритмов "распределения объектов по кластерам".
Существует точка зрения, что в отличие от многих других статистических процедур, методы кластерного анализа используются в большинстве случаев тогда, когда вы не имеете каких-либо априорных гипотез относительно классов, но все еще находитесь в описательной стадии исследования. Следует понимать, что кластерный анализ определяет "наиболее возможно значимое решение". Поэтому проверка статистической значимости в действительности здесь неприменима, даже в случаях, когда известны p-уровни (как, например, в методе K средних).

Области применения
Области применения

Техника кластеризации применяется в самых разнообразных областях. Хартиган (Hartigan, 1975) дал прекрасный обзор многих опубликованных исследований, содержащих результаты, полученные методами кластерного анализа. Например, в области медицины кластеризация заболеваний, лечения заболеваний или симптомов заболеваний приводит к широко используемым таксономиям. В области психиатрии правильная диагностика кластеров симптомов, таких как паранойя, шизофрения и т.д., является решающей для успешной терапии. В археологии с помощью кластерного анализа исследователи пытаются установить таксономии каменных орудий, похоронных объектов и т.д. Известны широкие применения кластерного анализа в маркетинговых исследованиях. В общем, всякий раз, когда необходимо классифицировать "горы" информации к пригодным для дальнейшей обработки группам, кластерный анализ оказывается весьма полезным и эффективным.

В начало

Объединение (древовидная кластеризация) Иерархическое дерево Меры расстояния Правила объединения или связи Общая логика
Объединение (древовидная кластеризация) Иерархическое дерево Меры расстояния Правила объединения или связи Общая логика

Приведенный в разделе Основная цель пример поясняет цель алгоритма объединения (древовидной кластеризации). Назначение этого алгоритма состоит в объединении объектов (например, животных) в достаточно большие кластеры, используя некоторую меру сходства или расстояние между объектами.

Типичным результатом такой кластеризации является иерархическое дерево. Иерархическое дерево
Иерархическое дерево

Рассмотрим горизонтальную древовидную диаграмму. Диаграмма начинается с каждого объекта в классе (в левой части диаграммы). Теперь представим себе, что постепенно (очень малыми шагами) вы "ослабляете" ваш критерий о том, какие объекты являются уникальными, а какие нет. Другими словами, вы понижаете порог, относящийся к решению об объединении двух или более объектов в один кластер.

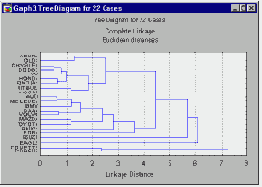
В результате, вы связываете вместе всё большее и большее число объектов и агрегируете (объединяете) все больше и больше кластеров, состоящих из все сильнее различающихся элементов. Окончательно, на последнем шаге все объекты объединяются вместе. На этих диаграммах горизонтальные оси представляют расстояние объединения (в вертикальных древовидных диаграммах вертикальные оси представляют расстояние объединения). Так, для каждого узла в графе (там, где формируется новый кластер) вы можете видеть величину расстояния, для которого соответствующие элементы связываются в новый единственный кластер. Когда данные имеют ясную "структуру" в терминах кластеров объектов, сходных между собой, тогда эта структура, скорее всего, должна быть отражена в иерархическом дереве различными ветвями. В результате успешного анализа методом объединения появляется возможность обнаружить кластеры (ветви) и интерпретировать их.

Меры расстояния
Меры расстояния

Объединение или метод древовидной кластеризации используется при формировании кластеров несходства или расстояния между объектами. Эти расстояния могут определяться в одномерном или многомерном пространстве. Например, если вы должны кластеризовать типы еды в кафе, то можете принять во внимание количество содержащихся в ней калорий, цену, субъективную оценку вкуса и т.д. Наиболее прямой путь вычисления расстояний между объектами в многомерном пространстве состоит в вычислении евклидовых расстояний. Если вы имеете двух- или трёхмерное пространство, то эта мера является реальным геометрическим расстоянием между объектами в пространстве (как будто расстояния между объектами измерены рулеткой).

Однако алгоритм объединения не "заботится" о том, являются ли "предоставленные" для этого расстояния настоящими или некоторыми другими производными мерами расстояния, что более значимо для исследователя; и задачей исследователей является подобрать правильный метод для специфических применений. Евклидово расстояние.
Евклидово расстояние.

Это, по-видимому, наиболее общий тип расстояния. Оно попросту является геометрическим расстоянием в многомерном пространстве и вычисляется следующим образом:

расстояние(x,y) = {

i (xi - yi)2 }1/2

Заметим, что евклидово расстояние (и его квадрат) вычисляется по исходным, а не по стандартизованным данным. Это обычный способ его вычисления, который имеет определенные преимущества (например, расстояние между двумя объектами не изменяется при введении в анализ нового объекта, который может оказаться выбросом). Тем не менее, на расстояния могут сильно влиять различия между осями, по координатам которых вычисляются эти расстояния. К примеру, если одна из осей измерена в сантиметрах, а вы потом переведете ее в миллиметры (умножая значения на 10), то окончательное евклидово расстояние (или квадрат евклидова расстояния), вычисляемое по координатам, сильно изменится, и, как следствие, результаты кластерного анализа могут сильно отличаться от предыдущих.

Квадрат евклидова расстояния.
Квадрат евклидова расстояния.

Иногда может возникнуть желание возвести в квадрат стандартное евклидово расстояние, чтобы придать большие веса более отдаленным друг от друга объектам. Это расстояние вычисляется следующим образом (см. также замечания в предыдущем пункте):

расстояние(x,y) =

i (xi - yi)2

Расстояние городских кварталов (манхэттенское расстояние).
Расстояние городских кварталов (манхэттенское расстояние).

Это расстояние является просто средним разностей по координатам. В большинстве случаев эта мера расстояния приводит к таким же результатам, как и для обычного расстояния Евклида. Однако отметим, что для этой меры влияние отдельных больших разностей (выбросов) уменьшается (так как они не возводятся в квадрат).

Манхэттенское расстояние вычисляется по формуле:

расстояние(x,y) =

i |xi - yi|

Расстояние Чебышева.
Расстояние Чебышева.

Это расстояние может оказаться полезным, когда желают определить два объекта как "различные", если они различаются по какой-либо одной координате (каким-либо одним измерением). Расстояние Чебышева вычисляется по формуле:

расстояние(x,y) = Максимум|xi - yi|

Степенное расстояние.
Степенное расстояние.

Иногда желают прогрессивно увеличить или уменьшить вес, относящийся к размерности, для которой соответствующие объекты сильно отличаются. Это может быть достигнуто с использованием степенного расстояния. Степенное расстояние вычисляется по формуле:

расстояние(x,y) = (

i |xi - yi|p)1/r

где r и p - параметры, определяемые пользователем. Несколько примеров вычислений могут показать, как "работает" эта мера. Параметр p ответственен за постепенное взвешивание разностей по отдельным координатам, параметр r ответственен за прогрессивное взвешивание больших расстояний между объектами. Если оба параметра - r и p, равны двум, то это расстояние совпадает с расстоянием Евклида.

Процент несогласия.
Процент несогласия.

Эта мера используется в тех случаях, когда данные являются категориальными. Это расстояние вычисляется по формуле:

расстояние(x,y) = (Количество xi

yi)/ i

Правила объединения или связи
Правила объединения или связи

На первом шаге, когда каждый объект представляет собой отдельный кластер, расстояния между этими объектами определяются выбранной мерой. Однако когда связываются вместе несколько объектов, возникает вопрос, как следует определить расстояния между кластерами? Другими словами, необходимо правило объединения или связи для двух кластеров. Здесь имеются различные возможности: например, вы можете связать два кластера вместе, когда любые два объекта в двух кластерах ближе друг к другу, чем соответствующее расстояние связи. Другими словами, вы используете "правило ближайшего соседа" для определения расстояния между кластерами; этот метод называется методом одиночной связи.

Это правило строит "волокнистые" кластеры, т.е. кластеры, " сцепленные вместе" только отдельными элементами, случайно оказавшимися ближе остальных друг к другу. Как альтернативу вы можете использовать соседей в кластерах, которые находятся дальше всех остальных пар объектов друг от друга. Этот метод называется метод полной связи. Существует также множество других методов объединения кластеров, подобных тем, что были рассмотрены. Одиночная связь (метод ближайшего соседа).
Одиночная связь (метод ближайшего соседа).

Как было описано выше, в этом методе расстояние между двумя кластерами определяется расстоянием между двумя наиболее близкими объектами (ближайшими соседями) в различных кластерах. Это правило должно, в известном смысле, нанизывать объекты вместе для формирования кластеров, и результирующие кластеры имеют тенденцию быть представленными длинными "цепочками".

Полная связь (метод наиболее удаленных соседей).
Полная связь (метод наиболее удаленных соседей).

В этом методе расстояния между кластерами определяются наибольшим расстоянием между любыми двумя объектами в различных кластерах (т.е. "наиболее удаленными соседями"). Этот метод обычно работает очень хорошо, когда объекты происходят на самом деле из реально различных "рощ". Если же кластеры имеют в некотором роде удлиненную форму или их естественный тип является "цепочечным", то этот метод непригоден.

Невзвешенное попарное среднее.
Невзвешенное попарное среднее.

В этом методе расстояние между двумя различными кластерами вычисляется как среднее расстояние между всеми парами объектов в них. Метод эффективен, когда объекты в действительности формируют различные "рощи", однако он работает одинаково хорошо и в случаях протяженных ("цепочного" типа) кластеров. Отметим, что в своей книге Снит и Сокэл (Sneath, Sokal, 1973) вводят аббревиатуру UPGMA для ссылки на этот метод, как на метод невзвешенного попарного арифметического среднего - unweighted pair-group method using arithmetic averages.

Взвешенное попарное среднее.
Взвешенное попарное среднее.

Метод идентичен методу невзвешенного попарного среднего, за исключением того, что при вычислениях размер соответствующих кластеров (т.е. число объектов, содержащихся в них) используется в качестве весового коэффициента. Поэтому предлагаемый метод должен быть использован (скорее даже, чем предыдущий), когда предполагаются неравные размеры кластеров. В книге Снита и Сокэла (Sneath, Sokal, 1973) вводится аббревиатура WPGMA для ссылки на этот метод, как на метод взвешенного попарного арифметического среднего - weighted pair-group method using arithmetic averages.

Невзвешенный центроидный метод.
Невзвешенный центроидный метод.

В этом методе расстояние между двумя кластерами определяется как расстояние между их центрами тяжести. Снит и Сокэл (Sneath and Sokal (1973)) используют аббревиатуру UPGMC для ссылки на этот метод, как на метод невзвешенного попарного центроидного усреднения - unweighted pair-group method using the centroid average.

Взвешенный центроидный метод (медиана).
Взвешенный центроидный метод (медиана).

тот метод идентичен предыдущему, за исключением того, что при вычислениях используются веса для учёта разницы между размерами кластеров (т.е. числами объектов в них). Поэтому, если имеются (или подозреваются) значительные отличия в размерах кластеров, этот метод оказывается предпочтительнее предыдущего. Снит и Сокэл (Sneath, Sokal 1973) использовали аббревиатуру WPGMC для ссылок на него, как на метод невзвешенного попарного центроидного усреднения - weighted pair-group method using the centroid average.

Метод Варда.
Метод Варда.

Этот метод отличается от всех других методов, поскольку он использует методы дисперсионного анализа для оценки расстояний между кластерами. Метод минимизирует сумму квадратов (SS) для любых двух (гипотетических) кластеров, которые могут быть сформированы на каждом шаге. Подробности можно найти в работе Варда (Ward, 1963). В целом метод представляется очень эффективным, однако он стремится создавать кластеры малого размера.

Для обзора других методов кластеризации, см. Двухвходовое объединение и Метод K средних.

В начало

Двувходовое объединение Вводный обзор Двувходовое объединение
Двувходовое объединение Вводный обзор Двувходовое объединение

Вводный обзор
Вводный обзор

Ранее этот метод обсуждался в терминах "объектов", которые должны быть кластеризованы (см. Объединение (древовидная кластеризация)). Во всех других видах анализа интересующий исследователя вопрос обычно выражается в терминах наблюдений или переменных. Оказывается, что кластеризация, как по наблюдениям, так и по переменным может привести к достаточно интересным результатам. Например, представьте, что медицинский исследователь собирает данные о различных характеристиках (переменные) состояний пациентов (наблюдений), страдающих сердечными заболеваниями. Исследователь может захотеть кластеризовать наблюдения (пациентов) для определения кластеров пациентов со сходными симптомами. В то же самое время исследователь может захотеть кластеризовать переменные для определения кластеров переменных, которые связаны со сходным физическим состоянием.

Двувходовое объединение
Двувходовое объединение

После этого обсуждения, относящегося к тому, кластеризовать наблюдения или переменные, можно задать вопрос, а почему бы не проводить кластеризацию в обоих направлениях? Модуль Кластерный анализ содержит эффективную двувходовую процедуру объединения, позволяющую сделать именно это. Однако двувходовое объединение используется (относительно редко) в обстоятельствах, когда ожидается, что и наблюдения и переменные одновременно вносят вклад в обнаружение осмысленных кластеров.

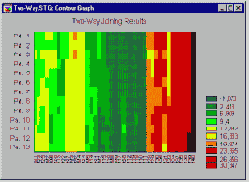
Так, возвращаясь к предыдущему примеру, можно предположить, что медицинскому исследователю требуется выделить кластеры пациентов, сходных по отношению к определенным кластерам характеристик физического состояния. Трудность с интерпретацией полученных результатов возникает вследствие того, что сходства между различными кластерами могут происходить из (или быть причиной) некоторого различия подмножеств переменных.

Поэтому получающиеся кластеры являются по своей природе неоднородными. Возможно это кажется вначале немного туманным; в самом деле, в сравнении с другими описанными методами кластерного анализа (см. Объединение (древовидная кластеризация) и Метод K средних), двувходовое объединение является, вероятно, наименее часто используемым методом. Однако некоторые исследователи полагают, что он предлагает мощное средство разведочного анализа данных (за более подробной информацией вы можете обратиться к описанию этого метода у Хартигана (Hartigan, 1975)).

В начало

Метод K средних Пример Вычисления Интерпретация результатов Общая логика
Общая логика

Этот метод кластеризации существенно отличается от таких агломеративных методов, как Объединение (древовидная кластеризация) и Двувходовое объединение. Предположим, вы уже имеете гипотезы относительно числа кластеров (по наблюдениям или по переменным). Вы можете указать системе образовать ровно три кластера так, чтобы они были настолько различны, насколько это возможно. Это именно тот тип задач, которые решает алгоритм метода K средних. В общем случае метод K средних строит ровно K различных кластеров, расположенных на возможно больших расстояниях друг от друга.

Пример
Пример

В примере с физическим состоянием (см. Двувходовое объединение), медицинский исследователь может иметь "подозрение" из своего клинического опыта, что его пациенты в основном попадают в три различные категории. Далее он может захотеть узнать, может ли его интуиция быть подтверждена численно, то есть, в самом ли деле кластерный анализ K средних даст три кластера пациентов, как ожидалось? Если это так, то средние различных мер физических параметров для каждого кластера будут давать количественный способ представления гипотез исследователя (например, пациенты в кластере 1 имеют высокий параметр 1, меньший параметр 2 и т.д.). Вычисления
Вычисления

С вычислительной точки зрения вы можете рассматривать этот метод, как дисперсионный анализ (см.

Дисперсионный анализ) "наоборот". Программа начинает с K случайно выбранных кластеров, а затем изменяет принадлежность объектов к ним, чтобы: (1) - минимизировать изменчивость внутри кластеров, и (2) - максимизировать изменчивость между кластерами. Данный способ аналогичен методу "дисперсионный анализ (ANOVA) наоборот" в том смысле, что критерий значимости в дисперсионном анализе сравнивает межгрупповую изменчивость с внутригрупповой при проверке гипотезы о том, что средние в группах отличаются друг от друга. В кластеризации методом K средних программа перемещает объекты (т.е. наблюдения) из одних групп (кластеров) в другие для того, чтобы получить наиболее значимый результат при проведении дисперсионного анализа (ANOVA). Интерпретация результатов
Интерпретация результатов

Обычно, когда результаты кластерного анализа методом K средних получены, можно рассчитать средние для каждого кластера по каждому измерению, чтобы оценить, насколько кластеры различаются друг от друга. В идеале вы должны получить сильно различающиеся средние для большинства, если не для всех измерений, используемых в анализе. Значения F-статистики, полученные для каждого измерения, являются другим индикатором того, насколько хорошо соответствующее измерение дискриминирует кластеры.

Компоненты дисперсии и смешанная модель ANOVA/ANCOVA

Основные идеи Свойства случайных эффектов Свойства компонент дисперсии Оценивание компонент дисперсии (технический обзор) Оценивание дисперсии случайных факторов Оценивание компонент дисперсии Проверка значимости компонент дисперсии Оценка внутриклассовой корреляции

Основные идеи
Основные идеи

В некоторых исследованиях иногда ошибочно предполагается, что достаточно только проделать некоторые действия с уровнями независимых переменных и оценить соответствующие отклики зависимых переменных. Независимые переменные, уровни которых определяются исследователем, называются фиксированными эффектами. Другой тип эффектов, часто вызывающий интерес исследователей, представляют случайные эффекты. Предполагается, что уровни фактора этого типа случайным образом выбраны из генеральной совокупности всех возможных уровней. В исследовательской работе иногда не представляется возможным осуществлять какие-либо действия с независимыми переменными, участвующими в анализе. Выходом является рассмотрение данных переменных как случайных. Например, генетический набор особей различных видов в настоящий момент не может быть полностью изменен в результате генетических экспериментов, поэтому генетик не имеет возможности полностью воссоздать картину воздействия различных комбинаций генов на здоровье, поведенческие характеристики и т.п. для обследуемой особи. В качестве еще одного примера, рассмотрим задачу производителя, который желает исследовать компоненты дисперсии характеристик какого-либо продукта, производящегося с помощью некоторого набора случайно выбранных станков, которыми управляли некоторые случайно выбранные операторы. Статистический анализ случайных эффектов основан на модели случайных эффектов, если все независимые переменные являются случайными эффектами, или на смешанной модели, если некоторые эффекты предполагаются случайными, а некоторые являются фиксированными.

Свойства случайных эффектов.
Свойства случайных эффектов.

Предположим, что вы располагаете данными об ущербе, который нанесен насекомыми-вредителями различным сортам зерновых. В данном эксперименте вы, по техническим причинам, не можете исследовать все существующие сорта зерновых, поэтому вы случайно выбираете из всей совокупности сортов зерновых только четыре сорта. Обследуется ущерб не более чем для четырех участков, на которых произрастает один из рассматриваемых сортов. Ущерб оценивается в баллах от 0 (нет ущерба) до 10 (огромный ущерб). Следующие данные представлены в работе Milliken и Johnson (1992, стр. 237). ДАННЫЕ: wheat.sta 3v СОРТ УЧАСТОК УЩЕРБ

A
A
A
B
B
B
B
C
C
C
C
D
D

1
2
3
4
5
6
7
8
9
10
11
12
13

3.90
4.05
4.25
3.60
4.20
4.05
3.85
4.15
4.60
4.15
4.40
3.35
3.80

Для определения компонент дисперсии по сопротивлению воздействию насекомым для переменных Сорт и Участок применим вначале модель дисперсионного анализа (ANOVA). Несколько неожиданным является то, что результаты для переменной Сорт в модели дисперсионного анализа совпадают для случая, когда данная переменная полагается фиксированным фактором, и для случая, когда данная переменная полагается случайным фактором (учитывая то, что используется сумма квадратов типа I, и зная, что переменная Сорт вычисляется первой). Таблица, следующая далее, показывает результаты анализа, смешанной модели ANOVA, в которой рассматривая переменную Сорт как фиксированный эффект, игнорируя переменную Участок (т.е., рассматривая вариацию участок на участок как меру случайной ошибки).

Итоги ANOVA: DAMAGE (wheat.sta)
Эффект Эффект
фикс/сл. сс
Эффект MS
Эффект сс
Ошибка MS
Ошибка
F
p {1} СОРТ

Fixed

.270053

.056435

4.785196

.029275

В той же модели можно рассматривать переменную Сорт как фиксированный эффект, а переменную Участок как случайный эффект. Таблица, представленная ниже, показывает результаты анализа данной смешанной модели.

Итоги ANOVA для объединенной ощибки: DAMAGE (wheat.sta) сс ошибка вычислена по методу Саттервейта
Эффект Эффект
фикс/сл. сс
Эффект MS
Эффект сс
Ошибка MS
Ошибка
F
p {1} СОРТ
{2} УЧАСТОК

фиксир.
случайн.

3
9

.270053
.056435

9
-----

.056435
-----

4.785196
-----

.029275
-----

В следующей таблице представлены результаты анализа модели со случайными эффектами, в которой обе переменные Участок и Сорт рассматриваются как случайные эффекты.

Итоги ANOVA для объединенной ощибки: DAMAGE (wheat.sta) сс ошибка вычислена по методу Саттервейта
Эффект Эффект
фикс/сл. сс
Эффект MS
Эффект сс
Ошибка MS
Ошибка
F
p {1} СОРТ
{2} УЧАСТОК

Random
Random

3
9

.270053
.056435

9
-----

.056435
-----

4.785196
-----

.029275
-----

Как следует из таблиц дисперсионного анализа, критерии значимости для переменной Сорт имеет один и тот же уровень для всех трех моделей. Однако если вычислить компоненты дисперсии, то различие между смешанной моделью (рассматривающей Участок как фиксированный эффект) и случайной моделью (рассматривающей Участок как случайный эффект) становится очевидна. Таблица, представленная ниже, показывает оценки компонент дисперсии для смешанной модели, рассматривающей переменную Участок как фиксированный эффект.

Компоненты дисперсии (wheat.sta) Тип средн. квадрата: 1 Источник DAMAGE

{2} УЧАСТОК
Ошибка

.056435
0.000000

Следующая таблица показывает оценки компонент дисперсии когда переменные Сорт и Участок рассматриваются как случайные эффекты.
Компоненты дисперсии (wheat.sta)

Компоненты дисперсии (wheat.sta) Тип средн. квадр.: 1 Источник DAMAGE

{1} СОРТ
{2} УЧАСТОК
Ошибка

.067186
.056435
0.000000

Очевидно, различие между данными наборами оценок состоит в том, что компонента дисперсии для переменной Сорт вычисляется только, если анализ проводится с помощью модели случайных эффектов. Это отражает основное отличие между фиксированным и случайными эффектами.

Предполагается, что вариация уровней случайного фактора является представительной для вариации популяции всевозможных уровней в целом. Таким образом, по наблюдаемым уровням фактора можно оценить его дисперсию. Еще более важным является то, что ковариация между уровнями случайного фактора и откликами зависимой переменной может быть использована для оценки компоненты дисперсии зависимой переменной, которая обусловлена рассматриваемым случайным фактором. Напротив вариация уровней фиксированных факторов произвольно выбирается исследователем (т.е. исследователь может выбрать столько уровней фиксированного фактора, сколько ему нужно). Следовательно, вариация фиксированного фактора не может быть использована ни для разумной оценки дисперсии, ни для разумной оценки ковариации. Имея в виду описанную разницу между фиксированными и случайными эффектами, рассмотрим более подробно особенности компонент дисперсии.

В начало

Свойства компонент дисперсии.
Свойства компонент дисперсии.

Следующий пример иллюстрирует применение языка STATISTICA BASIC, если у вас не имеется доступа к системе STATISTICA, вы можете воспользоваться любой другой язык программирования, (например, Visual BASIC). Чтобы лучше разобраться с понятием компонент дисперсии: сгенерируем файл данных с заранее известными компонентами дисперсии, затем с помощью модуля Компоненты дисперсии и смешанная модель ANOVA/ANCOVA оценим компоненты дисперсии рассматриваемых данных Создадим новый файл данных с 2 переменными и 500 наблюдениями. Затем составим следующую программу на языке STATISTICA BASIC .

NoGroups:=50;
NoCases:=500;
NPerGroup:=NoCases/NoGroups;
redim RandomEffects(NoGroups);

for ilevel:=1 to NoGroups do
     RandomEffects(ilevel):=Normal(2);

error:=1;
for i:=1 to ncases do begin
     ilevel:=trunc((i-1)/NPerGroup)+1;

data(i,1):=ilevel;

data(i,2):=RandomEffects(ilevel)
          +Normal(error);
end;

{ Данный массив будет содержать }
{ случайные эффекты на соответствующих}
{ уровнях зависимой переменной }
{ Здесь генерируются случайные эффекты, }
{ имеющие нормальное распределения со }
{ ст.откл. = 2, т.е. с дисперсией = 4 }

{ Сигма (и дисперсия) ошибки будет равна 1 }

{ В данной строке генерируются }
{ целые числа: 1-50, n=10 }

{ Запись чисел в первую переменную }

{Вычисление значений зависимой переменной: }
{ y(i)=СлучайныйЭффект(ilevel) + случ. ошибка }

Данная программа размещает числа от 1 до 50 в первую переменную рассматриваемого файла данных. Данные числа образуют 50 подвыборок по 10 элементов в каждой. Обратите внимание на то, что в начале программы случайные эффекты определяются как случайные числа, распределенные нормально с параметром стандартного отклонения равным 2 (дисперсия равна 2*2=4). Ошибка задается случайными числами, которые распределены по нормальному закону с параметром стандартного отклонения равным 1 (дисперсия равна 1). Затем, каждое значение зависимой переменной вычисляется как сумма двух случайных чисел, независимых и распределенных по нормальному закону, одно из данных чисел является значение ошибки, а другое обуславливает значение случайного эффекта (т.е. случайное число для соответствующего уровня случайного эффекта).

Когда вы будете анализировать созданные таким образом данные, рассматривая переменную 1 как случайный фактор и, вычисляя компоненты дисперсии (выберите любой метод оценки), то вы будете получать оценки обычно близкие к 4 для случайного фактора и к 1 для ошибки.

Если вы сочтете возможным немного поэкспериментировать с данной программой, например, рассмотреть меньшее количество подвыборок (например, три), то вы обнаружите существенное отклонение вычисляемых оценок от тех, которые были "зашиты" в программу (т.е. 4 и 1). Это иллюстрирует тот факт, что для небольшого количества выборок оценки компонент дисперсии недостаточно надежны, что является результатом увеличения ошибки. Вы можете использовать данную программу для исследования зависимости между числом уровней случайного фактора и надежностью оценок.

В начало

Оценивание компонент дисперсии (технический обзор)
Оценивание компонент дисперсии (технический обзор)

Основной целью оценивания компонент дисперсии является вычисление ковариации между случайными факторами и зависимой переменной. В зависимости от метода, выбранного для оценки компонент дисперсии, вычисляются дисперсии случайных факторов, а также критерии значимости, чтобы проверить являются ковариации между случайными факторами и зависимой переменной отличными от нуля.

Оценивание дисперсии случайных факторов.
Оценивание дисперсии случайных факторов.

Метод дисперсионного анализа (ANOVA) предоставляет интегрированный подход к оцениванию компонент дисперсии, так как позволяет оценить дисперсии случайных факторов, компоненты дисперсии зависимой переменной, обусловленные случайными факторами, а также проверить, значимо или нет компоненты дисперсии отличаются от нуля. Метод ANOVA начинает вычислять дисперсию случайных факторов с построения матрицы Суммы квадратов и смешанных произведений (SSCP) для независимых переменных. Из матрицы Суммы квадратов и смешанных произведений для независимых случайных факторов затем удаляется влияние фиксированных эффектов, оставляя, как это требуется для смешанной модели, случайные эффекты независимыми от фиксированных эффектов (см., например, Searle, Casella и McCulloch, 1992). Полученная таким образом матрица Сумм квадратов и смешанных произведений для каждого случайного фактора затем делится на соответствующее число степеней свободы с целью получить элементы матрицы Ожидаемый MS. Ненулевые внедиагональные элементы рассматриваемой матрицы для случайных эффектов отражают степень смешивания, которая должна быть учтена при вычислении дисперсии для каждого фактора. В файле wheat.sta, рассматривая переменные Сорт и Участок как случайные эффекты, обратите внимание на то, что соответствующий элемент матрицы Ожидаемый MS для этих двух факторов указывает на наличие некоторой степени смешивания. Ниже приведена таблица Ожидаемых средних квадратов. Ожидаемые средние квадраты (wheat.sta) Тип средн. квадр.: 1
Источник Эффект
фикс/сл.
СОРТ
УЧАСТОК
Ошибка {1} СОРТ
{2} УЧАСТОК
Ошибка

Случайн.
Случайн.

3.179487

1.000000
1.000000

1.000000
1.000000
1.000000

Элементы матрицы ожидаемых средних квадратов используются для оценки дисперсии случайных эффектов, приравниванием соответствующих значений дисперсий соответствующим значениям ожидаемых средних квадратов.

Например, оценка дисперсии для переменной Сорт, используя сумму квадратов типа I вычислялась бы как 3.179487 умножить на средний квадрат для переменной Сорт плюс 1, умноженная на средний квадрат для переменной Участок, плюс 1, умноженная на средний квадрат для Ошибки.

Однако подход дисперсионного анализа для вычисления компонент дисперсии, однако такой подход не лишен некоторых вычислительных проблем (т.е. оценки, полученные при использовании метода дисперсионного анализа, в общем случае являются смещенными, а также могут быть отрицательными, что противоречит определению дисперсии, которая всегда положительна). В качестве альтернативы модели дисперсионного анализа для получения оценок используется метод максимального правдоподобия. Метод максимального правдоподобия базируется на использовании квадратичных форм для оценки компонент дисперсии и обычно, хотя и не всегда, в нем применяется некоторая итеративная процедура для поиска решения. Возможно, самой простой разновидностью метода максимального правдоподобия является метод MIVQUE(0). MIVQUE(0) расшифровывается как метод, в результате применения которого получаются квадратичные несмещенные оценки с минимальной дисперсией (Minimum Variance Quadratic Unbiased Estimators). Так как в MIVQUE(0) отсутствует взвешивание случайных эффектов (поэтому 0 является аргументом MIVQUE), то итеративный поиск решения для оценки компонент дисперсии применять не надо. MIVQUE(0) в первую очередь вычисляет элементы матрицы Квадратичных сумм квадратов (SSQ). Элементы матрицы SSQ для случайных эффектов определяются как суммы квадратов сумм квадратов и смешанных произведений для каждого случайного эффектов в рассматриваемой модели (после исключения влияния фиксированных эффектов). Элементы данной матрицы сродни элементам матрицы ожидаемых средних квадратов, которая используется для оценки ковариаций между случайными факторами и зависимой переменной. Матрица SSQ для файла данных wheat.sta показана ниже. Обратите внимание на то, что ненулевые внедиагональные элементы для переменных Сорт и Участок вновь демонстрируют некоторую степень смешивания.

MIVQUE(0) Оценивание компонент дисперсии (wheat.sta) SSQ матр. Источник СОРТ УЧАСТОК Ошибка УЩЕБР {1} СОРТ
{2} УЧАСТОК
Ошибка

31.90533
9.53846
9.53846

9.53846
12.00000
12.00000

2.418964
1.318077
1.318077

Методы максимума правдоподобия и ограниченного максимума правдоподобия с точки зрения вычисления компонент дисперсии тесно связаны с MIVQUE(0). В данной программе методы МП и ограниченный МП используют оценки, полученные в результате работы метода MIVQUE(0), в качестве начальных входных параметров для соответствующей итеративной процедуры вычисления компонент дисперсии. Следовательно, элементы матрицы SSQ используются как стартовые оценки ковариаций между случайными факторами и зависимой переменной в методах МП и ограниченного МП.

В начало

Оценивание компонент дисперсии.
Оценивание компонент дисперсии.

Методы модели дисперсионного анализа для оценивания компонент дисперсии связаны с нахождением решения для системы уравнений, задающей соотношения между оцененными дисперсиями и ковариациями случайных факторов и оцененными ковариациями между случайными факторами и зависимой переменной. Решение такой системы определяет компоненты дисперсии. В таблице снизу показаны оценки сумм квадратов типа I для компонент дисперсии файла данных wheat.sta. Компоненты дисперсии (wheat.sta) Тип средн. квадр.: 1 Источник УЩЕРБ {1} СОРТ
{2} УЧАСТОК
Ошибка

0.067186
0.056435
0.000000

Компоненты дисперсии, полученные методом MIVQUE(0), вычисляются обращением соответствующей подматрицы матрицы SSQ, которая не включает зависимую переменную, с последующим умножением полученной матрицы на вектор-столбец зависимой переменной. Это равносильно решению системы уравнений, которая связывает зависимую переменную со случайными независимыми переменными, принимая во внимание ковариации между независимыми переменными. Результаты оценивания по методу MIVQUE(0) для файла данных wheat.sta представлены в следующей таблице.

MIVQUE(0) Оценка компонент дисперсии (wheat.sta) Компоненты дисперсии Источник УЩЕРБ {1} СОРТ
{2} УЧАСТОК
Ошибка

0.056376
0.065028
0.000000

Оценки компонент дисперсии для МП и ограниченного МП вычисляются в результате работы итеративной процедуры, которая последовательно оптимизирует оценки параметров для эффектов в модели. Ограниченный МП отличается от МП тем, что в данном методе максимум функции правдоподобия находится только для случайных эффектов, т.е. решение при ограничениях. В методах МП и ограниченного МП итеративное решение находится в результате подбора весов случайных эффектов, максимизирующих функцию правдоподобия на рассматриваемых данных. Результаты оценки по методу MIVQUE(0) используются как входные стартовые параметры для итерационных алгоритмов МП и ограниченного МП, поэтому данные три метода очень близки. Статистическая теория, лежащая в основе вычисления компонент дисперсии методом максимального правдоподобия, является достаточно продвинутой (работа Searle, Casella и McCulloch, 1992, рекомендуется в качестве авторитетного источника). Реализация алгоритмов максимального правдоподобия на практике связана с многочисленными вычислительными трудностями (см., например, Hemmerle & Hartley, 1973, а также Jenrich & Sampson, 1976, где описана реализация данных алгоритмов). Отметим, что трудности вычислительной реализации данных алгоритмов могут привести к получению оценок компонент дисперсии, которые могут лежать вне заданного пространства параметров, а также к сходимости к неоптимальным решениям или получению несостоятельных результатов. Milliken и Johnson (1992) отмечают все эти проблемы с коммерческим программным обеспечением, которое они использовали для вычисления компонент дисперсии.

Основная идея, лежащая в основе методов МП и ограниченного МП, состоит в том, что необходимо подобрать веса для случайных эффектов так, чтобы минимизировался взятый со знаком минус натуральный логарифм функции правдоподобия (поскольку, функция правдоподобия изменяется от 0 до 1, то, найдя минимум для ее натурального логарифма, взятого со знаком минус, мы найдем максимум функции правдоподобия). Значения логарифма функции правдоподобия в методе ограниченного МП и соответствующие оценки компонент дисперсии на каждом шаге итерации для файла данных wheat.sta вы найдете в таблице Отчет об итерациях, которая приведена ниже.

Отчет об итерациях (wheat.sta) Переменная: УЩЕРБ Итер. Лог правд. Ошибка СОРТ 1
2
3
4
5
6
7

-2.30618
-2.25253
-2.25130
-2.25088
-2.25081
-2.25081
-2.25081

.057430
.057795
.056977
.057005
.057006
.057003
.057003

.068746
.073744
.072244
.073138
.073160
.073155
.073155

Значения логарифма функции правдоподобия в методе МП и соответствующие оценки компонент дисперсии на каждом шаге итерации для файла данных wheat.sta вы найдете в таблице Отчет об итерациях, которая приведена ниже.

Отчет об итерациях (wheat.sta) Переменная: УЩЕРБ Итерация Лог LL Ошибка СОРТ 1
2
3
4
5
6

-2.53585
-2.48382
-2.48381
-2.48381
-2.48381
-2.48381

.057454
.057427
.057492
.057491
.057492
.057492

.048799
.048541
.048639
.048552
.048552
.048552

Как можно видеть, оценки для компонент дисперсии, полученные с помощью различных методов, очень похожи. В общем, компоненты дисперсии, полученные различными методами, согласуются достаточно хорошо (см., например, Swallow & Monahan, 1984).

В начало

Проверка значимости компонент дисперсии.
Проверка значимости компонент дисперсии.

Когда для оценивания параметров используются методы максимального правдоподобия, стандартные методы проверки значимости не применимы. В дисперсионном анализе для проверки значимости оценок применяется разложение сумм квадратов с последующим исследованием отношений средних квадратов, такая методика неприменима для квадратичных методов оценивания. Отметим также, что для модели дисперсионного анализа применяется стандартный метод проверки значимости оценок с учетом смешивания случайных эффектов. Для проверки значимости в смешанной и случайной модели оценка дисперсии ошибки должна быть построена так, чтобы все источники случайной дисперсии были бы учтены, за исключением дисперсии интересующего исследователя случайного эффекта. Такое построение производится методом синтеза знаменателя (Satterthwaite, 1946); данный метод осуществляет поиск линейных комбинаций возможных источников случайной дисперсии, которые выступают в качестве оценки ошибки, используемой для проверки значимости соответствующей оценки для рассматриваемого эффекта.

В таблице, приведенной ниже, вы найдете коэффициенты, которые получаются в результате поиска выше упомянутых линейных комбинаций, используемые для проверки случайных эффектов Сорт и Участок.

Синтез знаменателя: Коэффициенты (MS типа: 1) (wheat.sta) Объединенная MS ошибок является
комббинацией соотв. MS эффект Эффект Фикс/сл. СОРТ УЧАСТОК Ошибка {1} СОРТ
{2} УЧАСТОК

Случайн.
Случайн.

1.000000

Значения этих коэффициентов указывают на то, что средний квадрат для Сорта должен быть протестирован против среднего квадрата для Участка, а средний квадрат для Участка должен быть протестирован против среднего квадрата ошибки. Возвращаясь вновь к таблице ожидаемых средних квадратов, становится очевидным, что метод синтеза знаменателя правильно идентифицировал ошибку для проверки эффектов Сорт и Участок. Хотя мы рассмотрели достаточно простой пример, в более сложных случаях при наличии множественного смешивания между случайными эффектами метод синтез знаменателя может определить не столь очевидные с первого взгляда компоненты ошибки для тестирования оценок случайных эффектов.

При вычислении критериев значимости случайных эффектов отношения соответствующих Средних квадратов используются для вычисления F статистик и p-величин. Заметим, что в более сложных случаях степени свободы для случайных эффектов могут быть дробными, а не целыми, это обусловлено тем, что только часть источников дисперсии была использована для синтеза соответствующих компонент ошибки, при проверке значимости оценок случайных эффектов. Ниже представлена таблица результатов дисперсионного анализа (ANOVA) для случайных эффектов Сорт и Участок. Отметим, что для рассматриваемого простого примера результаты, полученные ранее дисперсионным анализом, который рассматривал Участок как случайный эффект, вложенный в Сорт, совпадают с результатами, приведенными ниже.

Итоги ANOVA для объединенной ошибки: УЩЕРБ (wheat.sta) сс ошибка вычислена по методу Саттервейта
Эффект Эффект
Фикс/сл. сс
Эффект MS
Эффект сс
Ошибка MS
Ошибка
F
p {1} СОРТ
{2} УЧАСТОК

фиксир.
случайн.

3
9

.270053
.056435

9
-----

.056435
-----

4.785196
-----

.029275
-----

Как показано в таблице, эффект Сорт значим с p < 0.05, но, как и предполагалось, эффект Участок не может быть проверен на значимость, так как является основным источником подобного анализа. Если бы имелись данные о разновидностях растений, высаженных на каждом участке, то проверка значимости эффекта Участок была бы возможна.

Критерии значимости компонент дисперсии для метода MIVQUE(0) в общем случае не могут быть построены, за исключением некоторых специальных случаев (см. Searle, Casella и McCulloch, 1992). Асимптотические (на больших выборках) критерии значимости компонент дисперсии для методов МП и ограниченного МП могут быть построены для оценок параметров на последнем шаге итерационного алгоритма. В таблице, представленной ниже, отображены результаты вычисления асимптотических (для больших выборок) тестов на значимость для оценок, полученных методом ограниченного МП на данных файла wheat.sta.

Оценки по методу ограниченного МП (wheat.sta) Переменная: УЩЕРБ
-2*Log(Правдоподобие)=4.50162399
Эффект Компон.
дисп. Асимпт.
Стд.ош. Асимпт.
z Асимпт.
p {1} СОРТ
Ошибка

.073155
.057003

.078019
.027132

.937656
2.100914

.348421
.035648

В таблице, представленной ниже, отображены результаты вычисления асимптотических (для больших выборок) тестов на значимость для оценок, полученных методом МП на данных файла wheat.sta.

Оценки по методу МП (wheat.sta) Переменная УЩЕРБ
-2*Log(Правдоподобие)=4.96761616
Эффект Компон.
дисп. Асимпт.
Стд.ош. Асимпт.
z Асимпт.
p {1} СОРТ
Ошибка

.048552
.057492

.050747
.027598

.956748
2.083213

.338694
.037232

Необходимо отметить, что асимптотические критерии значимости оценок компонент дисперсии, полученные методами МП и ограниченного МП, состоятельны только на больших выборках, что, очевидно, не так для данных файла wheat.sta. Для рассматриваемых данных оба теста указывают на то, что компонента дисперсии переменной Сорт не отличается значимо от нуля.

Основные сведения об использовании дисперсионного в линейных моделях см.в разделе Элементарные понятия статистики.

В начало

Оценка внутриклассовой корреляции.
Оценка внутриклассовой корреляции.

Заметим, что если разделить компоненты дисперсии для случайных эффектов в модели на сумму всех компонент (включая компоненту ошибки), то полученные числа (в виде процентов) являются коэффициентами внутриклассовой корреляции для соответствующих эффектов.

В начало

Логлинейный анализ в таблицах частот

Общее назначение Двумерные таблицы частот Многомерные таблицы частот Логлинейная модель Согласие Автоматическая полгонка модели

Общее назначение
Общее назначение

Одним из основных методов разведочного анализа данных является кросстабуляция. Например, в медицине можно табулировать частоты различных симптомов заболевания по возрасту и полу пациентов; в области образования можно табулировать число учащихся, покинувших среднюю школу в зависимости от возраста, пола и этнического происхождения; экономист может табулировать число банкротств в зависимости от вида промышленности, региона и начального капитала; исследователь спроса может табулировать предпочтения потребителя в зависимости от вида товара, возраста и пола и т.д. Во всех этих случаях результаты представляются в виде многовходовых (многомерных) таблиц частот, то есть в виде таблиц сопряженности с двумя или более факторами.

Логлинейный анализ предлагает более глубокие методы исследования этих таблиц. А именно, он позволяет проверить статистическую значимость (см. раздел Элементарные понятия статистики) различных факторов и взаимодействий, присутствующих в таблице сопряженности (например, пол, место жительства и т.п.).

Анализ соответствий является описательным/разведочным методом, созданным для анализа сложных таблиц, содержащих некоторые меры соответствий между переменными - столбцами и переменными - строками. Получаемые результаты содержат информацию, похожую по своей природе на результаты Факторного анализа. Они позволяют изучить структуру категориальных переменных, включенных в таблицу.

В начало

Двумерные таблицы частот
Двумерные таблицы частот

Обзор методов логлинейного анализа начнем с наиболее простой таблицы сопряженности 2 x 2. Представьте, что вы интересуетесь зависимостью между возрастом людей и сединой волос. Вы имеете выборку из 100 человек и определяете, у кого из них седые волосы. Вы также записываете примерный возраст людей. Результаты этого исследования представлены в таблице следующим образом:

Седые
волосы Возраст Всего до 40 лет от 40 и старше Нет
Да Всего

40 20	5 35	45 55
60	40	100

Это и есть простейшая таблица сопряженности 2 x 2 (название ее понятно: в таблице имеется две строки и два столбца, соответствующие двум сопряженным переменным, каждая из которых принимает два значения). Далее, в процессе интерпретации результатов этого маленького анализа, вы познакомитесь с терминологией, которая будет полезна при анализе более сложных таблицы.

Объясняющие переменные и переменные отклика.
Объясняющие переменные и переменные отклика.

В теории множественной регрессии и в дисперсионном анализе обычно различают независимые и зависимые переменные. Зависимые переменные, это те переменные, поведение которых исследователь пытается "объяснить", то есть он предполагает, что эти переменные зависят от независимых переменных и хочет эту зависимость (связь) оценить. Факторы в таблицах 2x2 могут также рассматриваться с этой точки зрения: рассмотрите цвет волос (седой, не седой) как зависимую переменную, а возраст - как независимую. Альтернативные термины, которые используются при анализе таблиц сопряженности (называемых иногда также кросс-таблицами) - это переменные отклика и объясняющие переменные, соответственно. Переменные отклика - это те переменные, которые изменяются в ответ на изменение объясняющих переменных. Поэтому в приведенной выше таблице цвет волос можно рассматривать как переменную отклика, а возраст - как объясняющую (независимую) переменную.

Подгонка маргинальных частот.
Подгонка маргинальных частот.

Вернемся теперь к анализу нашего примера таблицы. Вы можете спросить, как выглядела бы таблица, если бы между переменными не было зависимости (нулевая гипотеза). Не вдаваясь в детали, можно ожидать, что в таком случае частоты в каждой ячейке будут пропорциональны маргинальным частотам, т.е. частотам, расположенным на краях таблицы (строки и столбцы Всего). Для примера рассмотрим таблицу:

Седые
волосы Возраст Всего до 40 лет от 40 и старше Нет
Да Всего

27 33	18 22	45 55
60	40	100

Здесь маргинальные частоты показаны в отдельных ячейках по краям таблицы. Вы видите, что маргинальные частоты в последней строке равны сумме частот в столбцах (60 = 27+33, 40 = 18+22), а маргинальные частоты в последнем столбце равны сумме частот в строках (45 = 27+18, 55 = 33+22). Заметим далее, что 27/33=18/22=45/55 и 27/18=33/22=60/40. При заданных маргинальных частотах в ячейках содержатся частоты, которые следовало бы ожидать при отсутствии связи между возрастом и цветом волос. В отличие от данной таблицы, таблица, приведенная выше, показывает зависимость между двумя табулированными переменными. Для нее мы имеем соотношение: 40 > (40+5)*(40+20)/100 т.к. наблюдается меньше, чем ожидается при нулевой гипотезе, людей без седых волос при возрасте менее 40 лет и повышенное число людей с седыми волосами для возраста больше 40 лет. Другими словами, возраст и седина положительно связаны друг с другом.

Этот пример поясняет общий принцип, на котором основан логлинейный анализ: имея маргинальные суммы частоты для двух (или более) факторов вы можете вычислить частоты в ячейках, которые следовало бы ожидать при отсутствии связи между факторами. Статистически значимые отклонения наблюдаемых частот от ожидаемых указывают на зависимость между табулированными переменными.

Подход, основанный на подгонке модели.
Подход, основанный на подгонке модели.

Можно сказать, что подгонка модели для двух переменных (возраст и цвет волос) сводится к вычислению частот в ячейках таблицы на основании маргинальных частот (сумм по строкам и по столбцам). Значимые отклонения наблюдаемых частот от ожидаемых указывают на несогласие с гипотезой независимости двух переменных, т.е. на наличие связи (в данном примере на наличие связи (зависимости) между возрастом и цветом волос.

В начало

Многомерные таблицы частот
Многомерные таблицы частот

Рассуждения, проведенные для таблицы 2 на 2, можно обобщить на более сложные таблицы. Предположим, что имеется третья переменная, показывающая имели, или не имели люди, попавшие в выборку, стрессы на работе.

Так как вы интересуетесь влиянием стресса на цвет волос, переменную Стресс следует рассматривать как объясняющую. (Заметим, если "перевернуть" задачу и исследовать влияние седых волос на стресс, то стресс должен рассматриваться как отклик, а цвет волос будет уже объясняющей переменной.) В итоге мы получим таблицу частот с тремя входами.

Модель подгонки.
Модель подгонки.

Предыдущие рассуждения также применимы к анализу этой таблицы. Однако можно рассмотреть более сложные модели. Например, вы можете начать с гипотезы о независимости факторов. Как и ранее, ожидаемые частоты в этом случае должны соответствовать, т.е. быть пропорциональны, маргинальным частотам. Если возникают какие-либо значимые отклонения от этого соответствия (пропорциональности частот в ячейках и маргинальных частот), то гипотезу о независимости табулированных переменных следует отклонить.

Эффекты взаимодействия.
Эффекты взаимодействия.

Другой очевидной моделью является модель, в которой возраст и стресс связаны с цветом волос, но ни возраст, ни стресс не взаимодействуют в своем влиянии на цвет волос (иными словами, их влияние независимо). В этом случае нужно одновременно подобрать маргинальные суммы в двумерной (двухвходовой) таблице для возраста и цвета волос, полученной суммированием по уровням стресса, и для двумерной таблицы для стресса и цвета волос, полученной суммированием по уровням возраста. Если эта модель не согласуется с данными, то вы можете заключить, что возраст, стресс и цвет волос являются полностью взаимосвязанными (взаимозависимыми). Другими словами, что возраст и стресс взаимодействуют в своем влиянии на зависимую переменную.

Понятие взаимодействия, рассматриваемое здесь, аналогично к понятию взаимодействия в дисперсионном анализе. Например, взаимодействие возраста и стресса можно интерпретировать как изменение зависимости между возрастом и цветом волос под влиянием стресса. Хотя возраст приводит только к небольшому поседению в отсутствие стресса, он оказывает весьма большое влияние в присутствии стресса.

Другими словами, влияние возраста и стресса на поседение не аддитивно. Если вы не знакомы с концепцией взаимодействия, то можете прочитать об этом в разделе Вводный обзор главы Дисперсионный анализ. Интерпретация результатов логлинейного анализа многовходовых таблиц часто похожа на интерпретацию результатов дисперсионного анализа (ANOVA).

Итеративная пропорциональная подгонка.
Итеративная пропорциональная подгонка.

Вычисление ожидаемых частот значительно усложняется, когда таблица содержит более двух факторов. Тем не менее, они тоже могут быть вычислены, и поэтому, рассуждения, относительно таблиц типа 2x2 применимы к более сложным таблицам. Широко используемым методом вычисления ожидаемых частот является метод итеративной пропорциональной подгонки.

В начало

Логлинейная модель
Логлинейная модель

Термин логлинейный (или логарифмически-линейный) происходит из-за того, что с помощью логарифмического преобразования можно переформулировать задачу анализа многомерных таблиц частот в терминах дисперсионного анализа. В частности, многовходовую таблицу частот можно рассматривать как отражение различных главных и взаимодействующих влияний, которые складываются вместе линейным образом. Бишоп, Файенберг и Холланд (Bishop, Fienberg, Holland, 1974) приводят подробное описание того, каким образом можно вывести логлинейные уравнения, выражающие соотношения между факторами в многовходовых таблицах частот.

В начало

Согласие
Согласие

В предшествующем обсуждении была сделана ссылка на "значимость" отклонений наблюдаемых частот от ожидаемых. Можно вычислить статистическую значимость этого отклонения с помощью критерия хи-квадрат. Модуль Логлинейный анализ вычисляет два типа статистики хи-квадрат: традиционную статистику хи-квадрат Пирсона и статистику максимума отношения правдоподобия хи-квадрат (термин отношение правдоподобия был впервые использован в работе Neyman and Pearson, 1931; термин максимум правдоподобия был впервые использован в работе Fisher, 1922a).

На практике интерпретация этих двух статистик хи-квадрат в общем случае схожа. Оба критерия оценивают, являются ли ожидаемые частоты в ячейках для соответствующей модели значимо отличающимися от наблюдаемых частот или нет. Если отличие значимо, то гипотеза об отсутствии связей отвергается.

Просмотр и отображение остаточных частот.
Просмотр и отображение остаточных частот.

После того, как модель выбрана, хорошей идеей, конечно, является исследование остаточные частоты. По определению, остаточные частоты равны разности наблюдаемых и ожидаемых частот. Если модель согласуется с таблицей, все остаточные частоты будут представлять собой " остаточный шум", то есть, состоять из положительных и отрицательных значений примерно одинакового размаха, случайным образом распределенных по всем ячейкам таблицы.

Статистическая значимость эффектов.
Статистическая значимость эффектов.

Статистики хи-квадрат для моделей, связанных иерархически друг с другом или иерархически вкладывающихся друг в друга, могут сравниваться непосредственно. В общем случае, мы говорим, что две модели связаны иерархически друг с другом, если одна из них может быть получена из другой добавлением членов (переменных или взаимодействий) или путем их удаления (но не того и другого одновременно). Можно оценить разницу между статистиками хи-квадрат для двух моделей на основании разности между их степенями свободы. Если статистика хи-квадрат для разности значима, то можно заключить, что трехфакторная модель взаимодействия дает значимо лучшее согласие для наблюдаемой таблицы, чем модель без этого взаимодействия. Поэтому трехфакторное взаимодействие является статистически значимым.

В общем случае, две модели иерархически связаны друг с другом, если одна может быть получена из другой добавлением некоторых членов (переменных или взаимодействий) или удалением некоторых членов (но не тем и другим одновременно).

В начало

Автоматическая подгонка модели
Автоматическая подгонка модели

Когда анализируются четырехмерные таблицы или таблицы с большим числом измерений, нахождение наилучшей модели может оказаться достаточно трудоемким.

С целью облегчения поиска " хорошей модели" по имеющимся данным вы можете использовать автоматическую подгонку модели. Общая логика этого алгоритма следующая. Сначала программа подгоняет модель, в которой нет связей между факторами. Если она отвергается (т.е. соответствующая статистика хи-квадрат имеет значимую величину), то подгоняется модель со всеми возможными взаимодействиями двух факторов. Если эта модель тоже не принимается, то программа проверит модель со всеми трехфакторными взаимодействиями и т.д. Теперь предположим, что в ходе этого процесса установлено, что модель со всеми двухфакторными взаимодействиями подходит для имеющихся данных. Тогда программа начнет устранять двухфакторные взаимодействия, которые не являются статистически значимыми. Результирующей моделью станет такая модель, которая включает наименьшее необходимое для согласия число взаимодействующих факторов.

В начало

Методы добычи данных

Понятие добычи данных Хранилища данных Опертивная аналитическая обработка данных (OLAP) Разведочный анализ данных (РАД) и методы добычи данных РАД и проверка гипотез Вычислительные методы РАД Графические методы РАД (визуализация данных) Проверка результатов РАД Нейронные сети

Понятие "добыча данных" (Data Mining)

StatSoft определяет понятие "добыча данных" как процесс аналитического исследования больших массивов информации (обычно экономического характера) с целью выявления определенных закономерностей и систематических взаимосвязей между переменными, которые затем можно применить к новым совокупностям данных. Этот процесс включает три основных этапа: исследование, построение модели или структуры и ее проверку. В идеальном случае, при достаточном количестве данных можно организовать итеративную процедуру для построения устойчивой (робастной) модели. В то же время, в реальной ситуации практически невозможно проверить экономическую модель на стадии анализа и поэтому начальные результаты имеют характер эвристик, которые можно использовать в процессе принятия решения (например, "Имеющиеся данные свиделельствуют о том, что у женщин частота приема снотворных средств увеличивается с возрастом быстрее, чем у мужчин.").

Методы добычи данных приобретают все большую популярность в качестве инструмента для анализа экономической информации, особенно в тех случаях, когда предполагается, что из имеющихся данных можно будет извлечь знания для принятия решений в условиях неопределенности. Хотя в последнее время возрос интерес к разработке новых методов анализа данных, специально предназначенных для сферы бизнеса (например, Деревья классификации), в целом системы добычи данных по-прежнему основываются на классических принципах разведочного анализа данных (РАД) и построения моделей и используют те же подходы и методы.

Имеется, однако, важное отличие процедуры добычи данных от классического разведочного анализа данных (РАД) : системы добычи данных в большей степени ориентированы на практическое приложение полученных результатов, чем на выяснение природы явления. Иными словами, при добыче данных нас не очень интересует конкретный вид зависимостей между переменными задачи. Выяснение природы участвующих здесь функций или конкретной формы интерактивных многомерных зависимостей между переменными не является главной целью этой процедуры. Основное внимание уделяется поиску решений, на основе которых можно было бы строить достоверные прогнозы. Таким образом, в области добычи данных принят такой подход к анализу данных и извлечению знаний, который иногда характеризуют словами "черный ящик". При этом используются не только классические приемы разведочного анализа данных, но и такие методы, как нейронные сети , которые позволяют строить достоверные прогнозы, не уточняя конкретный вид тех зависимостей, на которых такой прогноз основан.

Очень часто добыча данных трактуется как "смесь статистики, методов искуственного интеллекта (ИИ) и анализа баз данных" (Pregibon, 1997, p. 8), и до последнего времени она не признавалась полноценной областью интереса для специалистов по статистике, а порой ее даже называли "задворками статистики" (Pregibon, 1997, p. 8). Однако, благодаря своей большой практической значимости, эта проблематика ныне интенсивно разрабатывается и привлекает большой интерес (в том числе и в ее статистических аспектах), и в ней достигнуты важные теоретические результаты (см. например, материалы ежегодно проводимой Международной конференции по поиску знаний и добыче данных( International Conferences on Knowledge Discovery and Data Mining), одним из организаторов которой в 1997 году стала Американская статистическая ассоциация - American Statistical Association).

Информацию по методам добычи данных можно найти в разделах Разведочный анализ данных и Нейронные сети; подробный обзор и обсуждение этой проблематики см.

в работах Fayyad, Piatetsky-Shapiro, Smyth & Uthurusamy (1996). Большой набор статей по этой тематике имеется в журнале Proceedings from the American Association of Artificial Intelligence Workshops on Knowledge Discovery in Databases published by AAAI Press (см. в частности, Piatetsky-Shapiro, 1993; Fayyad & Uthurusamy, 1994).

Добыча данных часто рассматривается как естественное развитие концепции хранилищ данных (см. далее).

В начало

Хранилища данных (Data Warehousing)
Хранилища данных (Data Warehousing)

StatSoft определяет понятие хранилища данных как способ хранения больших многомерных массивов данных, который позволяет легко извлекать и использовать информацию в процедурах анализа.

Эффективная архитектура хранилища данных должна быть организована таким образом, чтобы быть составной частью информационной системы управления предприятием (или по крайней мере иметь связь со всеми доступными данными). При этом необходимо использовать специальные технологии работы с корпоративными базами данных (например, Oracle, Sybase, MS SQL Server). Высокопроизводительная технология хранилищ данных, позволяющая пользователям организовать и эффективно использовать базу данных предприятия практически неограниченной сложности, разработана компанией StatSoft enterprise systems и называется SENS [STATISTICA Enterprise System] и SEWSS [STATISTICA Enterprise-Wide SPC System]).

В начало

Оперативная аналитическая обработка данных (OLAP)
Оперативная аналитическая обработка данных (OLAP)

Термин OLAP (или FASMI - быстрый анализ распределенной многомерной информации) обозначает методы, которые дают возможность пользователям многомерных баз данных в реальном времени генерировать описательные и сравнительные сводки ("views") данных и получать ответы на различные другие аналитические запросы. Обратите внимание, что несмотря на свое название, этот метод не подразумевает интерактивную обработку данных (в режиме реального времени); он означает процесс анализа многомерных баз данных (которые, в частности, могут содержать и динамически обновляемую информацию) путем составления эффективных "многомерных" запросов к данным различных типов. Средства OLAP могут быть встроены в корпоративные (масштаба предприятия) системы баз данных и позволяют аналитикам и менеджерам следить за ходом и результативностью своего бизнеса или рынка в целом (например, за различными сторонами производственного процесса или количеством и категориями совершенных сделок по разным регионам). Анализ, проводимый методами OLAP может быть как простым (например, таблицы частот, описательные статистики, простые таблицы), так и достаточно сложным (например, он может включать сезонные поправки, удаление выбросов и другие способы очистки данных).

Хотя методы добычи данных можно применять к любой, предварительно не обработанной и даже неструктурированной информации, их можно также использовать для анализа данных и отчетов, полученных средствами OLAP, с целью более углубленного исследования, как правило, в более высоких размерностях. В этом смысле методы добычи данных можно рассматривать как альтернативный аналитический подход (служащий иным целям, нежели OLAP) или как аналитическое расширение систем OLAP.

В начало

Разведочный анализ данных (РАД)
Разведочный анализ данных (РАД)

РАД и проверка гипотез
РАД и проверка гипотез

В отличие от традиционной проверки гипотез, предназначенной для проверки априорных предположений, касающихся связей между переменными (например, "Имеется положительная корреляция между возрастом человека и его/ее нежеланием рисковать"), разведочный анализ данных (РАД) применяется для нахождения связей между переменными в ситуациях, когда отсутствуют (или недостаточны) априорные представления о природе этих связей. Как правило, при разведочном анализе учитывается и сравнивается большое число переменных, а для поиска закономерностей используются самые разные методы. Вычислительные методы РАД
Вычислительные методы РАД

Вычислительные методы разведочного анализа данных включают основные статистические методы, а также более сложные, специально разработанные методы многомерного анализа, предназначенные для отыскания закономерностей в многомерных данных. Основные методы разведочного статистического анализа.
Основные методы разведочного статистического анализа.

К основным методам разведочного статистического анализа относится процедура анализа распределений переменных (например, чтобы выявить переменные с несимметричным или негауссовым распределением, в том числе и бимодальные), просмотр корреляционных матриц с целью поиска коэффициентов, превосходящих по величине определенные пороговые значения (см. предыдущий пример), или анализ многовходовых таблиц частот (например, "послойный" последовательный просмотр комбинаций уровней управляющих переменных).

Методы многомерного разведочного анализа.
Методы многомерного разведочного анализа.

Методы многомерного разведочного анализа специально разработаны для поиска закономерностей в многомерных данных (или последовательностях одномерных данных). К ним относятся: кластерный анализ, факторный анализ, анализ лискриминантных функций, многомерное шкалирование, логлинейный анализ, канонические корреляции, пошаговая линейная и нелинейная (например, логит) регрессия, анализ соответствий, анализ временных рядов и деревья классификации.

Нейронные сети.
Нейронные сети.

Этот класс аналитических методов основан на идее воспроизведения процессов обучения мыслящих существ (как они представляются исследователям) и функций нервных клеток. Нейронные сети могут прогнозировать будущие значения переменных по уже имеющимся значениям этих же или других переменных, предварительно осуществив процесс так называемого обучения на основе имеющихся данных.

Дополнительную информацию см. в разделе Нейронные сети; а также в модуле STATISTICA Neural Networks.

Графические методы РАД (визуализация данных)
Графические методы РАД (визуализация данных)

Широкий набор мощных методов разведочного анализа данных представлен также средствами графической визуализации данных. С их помощью можно находить зависимости, тренды и смещения, "скрытые" в неструктурированных наборах данных. Закрашивание.
Закрашивание.

Возможно, самым распространенным и исторически первым из методов, которые с полным основанием можно отнести к графическому разведочному анализу данных, стало закрашивание - интерактивный метод, позволяющий пользователю выбирать на экране компьютера отдельные точки-наблюдения или группы таких точек, находить их характеристики (в том числе общие) и изучать влияние отдельных наблюдений на соотношения между различными переменными . Эти соотношения между переменными также могут быть визуализированы с помощью подгоночных функций (например, прямыми в двумерном или поверхностями в трехмерном случае) вместе с соответствующими доверительными интервалами, и, таким образом, пользователь может в интерактивном режиме исследовать изменения параметров этих функций, временно удаляя или добавляя фрагменты набора данных.

С помощью закрашивания, например, можно выбрать (выделить) на одной из матричных диаграмм рассеяния все точки данных, принадлежащие определенной категории, На следующем рисунке, например, на четвертом графике в первом ряду выделены точки, соответствущие "среднему" уровню дохода.

Таким образом можно определить, как эти наблюдения влияют на взаимосвязи между другими переменными этого набора данных (например, на корреляцию между переменными "debt" и "assets" ). В режиме "динамического закрашивания" или "автоматического обновления функции подгонки" можно задать движение кисти по определенным последовательным диапазонам выбранной переменной (например, по непрерывным значениям переменной "income" или по ее дискретным значениям, как показано на предыдущем рисунке) и исследовать динамику вклада этой переменной в связи между другими переменными текущего набора данных.

Другие графические методы РАД.
Другие графические методы РАД.

К другим аналитическим графическим методам относятся подгонка и построение функций, сглаживание данных, наложение и объединение нескольких изображений, категоризация данных, расщепление или слияние подгрупп данных на графике, агрегирование данных, идентификация и маркировка подгрупп данных, удовлетворяющих определенным условиям, построение пиктографиков,

штриховка, построение доверительных интервалов и областей (например, эллипсов),

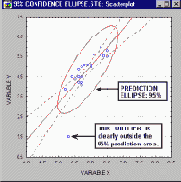
создание мозаичных структур, спектральных плоскостей,

послойное сжатие,

а также использование карт линий уровня, методов редукции выборки, интерактивного (и динамического) вращения

и динамического расслоения трехмерных изображений, выделение определенных наборов и блоков данных.

Проверка результатов РАД
Проверка результатов РАД

Предварительное исследование данных может служить лишь первым этапом в процессе их анализа, и пока результаты не подтверждены (методами кросс-проверки) на других фрагментах базы данных или на независимом множестве данных, их можно воспринимать самое большее как гипотезу.

Если результаты разведочного анализа говорят в пользу некоторой модели, то ее правильность можно затем проверить, применив ее к новым данных и определив степень ее согласованности с данными (проверка "способности к прогнозированию"). Для быстрого выделения различных подмножеств данных (например, для очистки, проверки и пр.) и оценки надежности результатов удобно пользоваться условиями выбора наблюдений.

В начало

Нейронные сети
Нейронные сети

Нейронные сети - это класс аналитических методов, построенных на (гипотетических) принципах обучения мыслящих существ и функционирования мозга и позволяющих прогнозировать значения некоторых переменных в новых наблюдениях по данным других наблюдений (для этих же или других переменных) после прохождения этапа так называемого обучения на имеющихся данных. Нейроные сети являются одним из методов так называемой добычи данных.

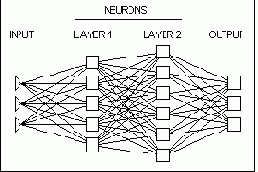
При применении этих методов прежде всего встает вопрос выбора конкретной архитектуры сети (числа "слоев" и количества "нейронов" в каждом из них). Размер и структура сети должны соответствовать (например, в смысле формальной вычислительной сложности) существу исследуемого явления. Поскольку на начальном этапе анализа природа явления обычно не бывает хорошо известна, выбор архитектуры является непростой задачей и часто связан с длительным процессом "проб и ошибок" (однако, в последнее время стали появляться нейронно-сетевые программы, в которых для решения этой трудоемкой задачи поиска "наилучшей" архитектуры сети применяются методы искусственного интеллекта).

Затем построенная сеть подвергается процессу так называемого "обучения". На этом этапе нейроны сети итеративно обрабатывают входные данных и корректируют свои веса таким образом, чтобы сеть наилучшим образом прогнозировала (в традиционных терминах следовало бы сказать "осуществляла подгонку") данные, на которых выполняется "обучение". После обучения на имеющихся данных сеть готова к работе и может использоваться для построения прогнозов.

"Сеть", полученная в результате "обучения", выражает закономерности, присутствующие в данных. При таком подходе она оказывается функциональным эквивалентом некоторой модели зависимостей между переменными, подобной тем, которые строятся в традиционном моделировании. Однако, в отличие от традиционных моделей, в случае "сетей" эти зависимости не могут быть записаны в явном виде, подобно тому как это делается в статистике (например, "A положительно коррелировано с B для наблюдений, у которых величина C мала, а D - велика"). Иногда нейронные сети выдают прогноз очень высокого качества; однако, они представляют собой типичный пример нетеоретического подхода к исследованию (иногда это называют "черным ящиком"). При таком подходе мы сосредотачиваемся исключительно на практическом результате - в данном случае - на точности прогнозов и их прикладной ценности, - а не на сути механизмов, лежащих в основе явления, или соответствии полученных результатов какой-либо имеющейся "теории".

Следует, однако, отметить, что методы нейронных сетей могут применяться и в таких исследованиях, где целью является построение объясняющей модели явления, поскольку нейронные сети помогают изучать данные на предмет поиска значимых переменных или групп таких переменных, и полученные результаты могут облегчить процесс последующего построения модели. Более того, сейчас имеются нейросетевые программы, которые с помощью сложных алгоритмов могут находить наиболее важные входные переменные, что уже непосредственно помогает строить модель.

Одно из главных преимуществ нейронные сетей состоит в том, что они, по крайней мере теоретически, могут аппроксимировать любую непрерывную функцию, и поэтому исследователю нет необходимости заранее принимать какие-либо гипотезы относительно модели, и даже - в ряде случаев - о том, какие переменные действительно важны. Однако, существенным недостатком нейронных сетей является то обстоятельство, что окончательное решение зависит от начальных установок сети и, как уже говорилось выше, его практически невозможно "интерпретировать" в традиционных аналитических терминах, которые обычно применяются при построении теории явления.

Некоторые авторы отмечают тот факт, что нейронные сети используют или, точнее, предполагают использование вычислительных систем с массовым параллелизмом. Например Haykin (1994, p. 2) определяет нейронную сеть как

"процессор с массивным распараллеливанием операций, обладающий естественной способностью сохранять экспериментальные знания и делать их доступными для последующего использования. Он похож на мозг в двух отношениях: (1) сеть приобретает знания в результате процесса обучения и (2) для хранения информации используются величины интенсивности межнейронных соединений, которые называются синаптическими весами". (p. 2).

Однако, как отмечает Ripley (1996), большинство существующих нейросетевых программ работают на однопроцессорных компьютерах. По его мнению, существенное ускорение работы может быть достигнуто не только за счет разработки программного обеспечения, использующего преимущества многопроцессорных систем, но также путем разработки более эффективных алгоритмов обучения.

Нейронные сети - это один из методов, применяемых для так называемой добычи данных; см. также Разведочный анализ данных. Дополнительную информацию по нейронным сетям можно найти в работах Haykin (1994), Masters (1995), Ripley (1996) и Welstead (1994). Относительно характеристик нейронных сетей как инструмента статистического анализа см. работу Warner и Misra (1996). См. также описание модуля STATISTICA Neural Networks.

В начало

Многомерное шкалирование

Общая цель Логика многомерного шкалирования Вычислительные методы Задание размерности пользователем Интерпретация осей координат Приложения Многомерное шкалирование и факторный анализ

Общая цель

Общая цель

Многомерное шкалирование (МНШ) можно рассматривать как альтернативу факторному анализу (см. Факторный анализ). Целью последнего, вообще говоря, является поиск и интерпретация "латентных (т.е. непосредственно не наблюдаемых) переменных", дающих возможность пользователю объяснить сходства между объектами, заданными точками в исходном пространстве признаков. Для определенности и краткости, далее, как правило, будем говорить лишь о сходствах объектов, имея ввиду, что на практике это могут быть различия, расстояния или степени связи между ними. В факторном анализе сходства между объектами (например, переменными) выражаются с помощью матрицы (таблицы) коэффициентов корреляций. В методе МНШ дополнительно к корреляционным матрицам, в качестве исходных данных можно использовать произвольный тип матрицы сходства объектов. Таким образом, на входе всех алгоритмов МНШ используется матрица, элемент которой на пересечении ее i-й строки и j-го столбца, содержит сведения о попарном сходстве анализируемых объектов (объекта [i] и объекта [j]). На выходе алгоритма МНШ получаются числовые значения координат, которые приписываются каждому объекту в некоторой новой системе координат (во "вспомогательных шкалах", связанных с латентными переменными, откуда и название МНШ), причем размерность нового пространства признаков существенно меньше размерности исходного (за это собственно и идет борьба).

В начало

Логика многомерного шкалирования

Логика многомерного шкалирования

Логику МНШ можно проиллюстрировать на следующем простом примере. Предположим, что имеется матрица попарных расстояний (т.е. сходства некоторых признаков) между крупными американскими городами. Анализируя матрицу, стремятся расположить точки с координатами городов в двумерном пространстве (на плоскости), максимально сохранив реальные расстояния между ними.
Полученное размещение точек на плоскости впоследствии можно использовать в качестве приближенной географической карты США.

В общем случае метод МНШ позволяет таким образом расположить "объекты" (города в нашем примере) в пространстве некоторой небольшой размерности (в данном случае она равна двум), чтобы достаточно адекватно воспроизвести наблюдаемые расстояния между ними. В результате можно "измерить" эти расстояния в терминах найденных латентных переменных. Так, в нашем примере можно объяснить расстояния в терминах пары географических координат Север/Юг и Восток/Запад.

Ориентация осей координат.
Ориентация осей координат.

Как и в Факторном анализе, ориентация осей может быть выбрана произвольной. Возвращаясь к нашему примеру, можно поворачивать карту США произвольным образом, но расстояния между городами при этом не изменятся. Таким образом, окончательная ориентация осей на плоскости или в пространстве является, в большей степени результатом содержательного решения в конкретной предметной области (т.е. решением пользователя, который выберет такую ориентацию осей, которую легче всего интерпретировать). В примере можно было бы выбрать ориентацию осей, отличающуюся от пары Север/Юг и Восток/Запад, однако последняя удобнее, как "наиболее осмысленная" и естественная.

В начало

Вычислительные методы

Вычислительные методы

Многомерное шкалирование - это не просто определенная процедура, а скорее способ наиболее эффективного размещения объектов, приближенно сохраняющий наблюдаемые между ними расстояния. Другими словами, МНШ размещает объекты в пространстве заданной размерности и проверяет, насколько точно полученная конфигурация сохраняет расстояния между объектами. Говоря более техническим языком, МНШ использует алгоритм минимизации некоторой функции, оценивающей качество получаемых вариантов отображения.

Меры качества отображения:
Меры качества отображения:

стресс. Мерой, наиболее часто используемой для оценки качества подгонки модели (отображения), измеряемого по степени воспроизведения исходной матрицы сходств, является так называемый стресс.

Величина стресса Phi в для текущей конфигурации определяется так:

Phi =

[dij - f (

ij)]2

Здесь dij - воспроизведенные расстояния в пространстве заданной размерности, а

ij (дельтаij) - исходное расстояние. Функция f (

ij) обозначает неметрическое монотонное преобразование исходных данных (расстояний). Таким образом, МНШ воспроизводит не количественные меры сходств объектов, а лишь их относительный порядок.

Обычно используется одна из несколько похожих мер сходства. Тем не менее, большинство из них сводится к вычислению суммы квадратов отклонений наблюдаемых расстояний (либо их некоторого монотонного преобразования) от воспроизведенных расстояний. Таким образом, чем меньше значение стресса, тем лучше матрица исходных расстояний согласуется с матрицей результирующих расстояний.

Диаграмма Шепарда.
Диаграмма Шепарда.

Можно построить для текущей конфигурации точек график зависимости воспроизведенных расстояния от исходных расстояний. Такая диаграмма рассеяния называется диаграммой Шепарда. По оси ординат OY показываются воспроизведенные расстояния (сходства), а по оси OX откладываются истинные сходства (расстояния) между объектами (отсюда обычно получается отрицательный наклон). На этом график также строится график ступенчатой функции. Ее линия представляет так называемые величины D-с крышечкой, то есть, результат монотонного преобразования f(

) исходных данных. Если бы все воспроизведенные результирующие расстояния легли на эту ступенчатую линию, то ранги наблюдаемых расстояний (сходств) был бы в точности воспроизведен полученным решением (пространственной моделью). Отклонения от этой линии показывают на ухудшение качества согласия (т.е. качества подгонки модели).

В начало

Задание размерности пользователем

Задание размерности пользователем

Если вы уже знакомы с факторным анализом, вы вполне можете пропустить этот раздел. В противном случае вы можете перечитать раздел Факторный анализ. Однако это не является необходимым для понимания идей многомерного шкалирования.

Вообще говоря, чем больше размерность пространства, используемого для воспроизведения расстояний, тем лучше согласие воспроизведенной матрицы с исходной (меньше значение стресса). Если взять размерность пространства равной числу переменных, то возможно абсолютно точное воспроизведение исходной матрицы расстояний. Однако нашей целью является упрощение решаемой задачи, с тем, чтобы объяснить матрицу сходства (расстояний) в терминах лишь нескольких важнейших факторов (латентных переменных или вспомогательных шкал). Возвращаясь к нашему примеру с расстояниями между городами, если получена двумерная карта, намного проще представить себе расположение городов и планировать передвижение между ними, чем если бы имелась только матрица попарных расстояний.

Причины плохого качества отображения.
Причины плохого качества отображения.

Обсудим, почему уменьшение числа факторов (или вспомогательных шкал) может приводить к ухудшению представления исходной матрицы. Обозначим буквами A, B, C и D, E, F две тройки городов. Соответствующие им точки и попарные расстояния между ними показаны в двух табличках (матрицах).

A B C D E F A
B
C D
E
F

0
90
90

0
90

0
90
180

0
90

Первой матрице соответствует случай когда города удалены друг от друга в точности на 90 километров, а второй - когда города D и F удаляются на 180 километров. Можно ли три точки, соответствующие городам (объектам) расположить в одномерном пространстве (на прямой)? Действительно, три точки, соответствующие городам D, E и F могут быть расположены на прямой линии:

D---90 км---E---90 км---F

D удален на 90 км от города E, и E - на 90 км от F, а город D удален на 90+90=180 км от F. Если попытаться проделать тоже самое с городами A, B и C, то видно, что соответствующие им точки уже нельзя разместить на прямой с сохранением исходной структуры расстояний. Однако эти точки можно расположить на плоскости, например, в виде треугольника:

A
90 км		90 км
B	90 км	C

Располагая эти три точки так, можно в точности воспроизвести все расстояния между ними.

Без лишних деталей, этот пример показывает, как конкретная матрица расстояний (сходств) связана с числом искомых латентных переменных (размерностью результирующего пространства). Конечно, "реальные" данные никогда не являются такими "точными", и содержат случайный шум, т.е. случайную изменчивость, влияющую на различие между воспроизведенной и исходной матрицей.

Критерий "каменистой осыпи".
Критерий "каменистой осыпи".

Обычно, для выбора размерности пространства, в котором будет воспроизводится наблюдаемая матрица, используют график зависимости стресса от размерности (график каменистой осыпи). Этот критерий впервые был предложен Кэттелом (Cattell (1966)) в контексте решения задачи снижения размерности в факторном анализе (см. Факторный анализ); Краскал и Виш (Kruskal and Wish (1978; стр. 53-60)) обсуждали применение этого графика в методе МНШ.

Кэттел предложил найти такую абсциссу на графике (в методе ФА, по оси абсцисс идут собственные значения), в которой график стресса начинает визуально сглаживаться в направлении правой, пологой его части, и, таким образом, уменьшение стресса максимально замедляется. Образно говоря, линия на рисунке напоминает скалистый обрыв, а черные точки на графике напоминают камни, которые ранее упали вниз. Таким образом, внизу наблюдается как бы каменистая осыпь из таких точек. Справа от выбранной точки на оси абсцисс, лежит только "факторная осыпь". Согласно этому критерию, на приведенном рисунке, скорее всего, следует выбрать для воспроизведения двумерное пространство.

Интерпретируемость конфигурации.
Интерпретируемость конфигурации.

Вторым критерием для решения вопроса о размерности с целью интерпретации является "ясность" полученной конфигурации точек. Иногда, как в нашем примере с городами, результирующие координаты легко интерпретируются. В других случаях, точки на графике могут образовывать ту или иную разновидность "случайного облака", и не существует непосредственного способа для интерпретации латентных переменных.

В последнем случае следует постараться немного увеличить число координатных осей и рассмотреть получаемые в результате конфигурации. Чаще всего, получаемые решения проще удается проинтерпретировать. Однако если точки на графике не следуют какому-либо образцу, а также если график стресса не показывает какого-либо явного "изгиба" (и не похож на "край обрыва"), то данные скорее всего являются случайным "шумом".

В начало

Интерпретация осей координат

Интерпретация осей координат

Интерпретация осей обычно представляет собой заключительный этап анализа по методу многомерного шкалирования. Как уже упоминалось ранее, в принципе, ориентация осей в методе МНШ может быть произвольной, и систему координат можно повернуть в любом направлении. Поэтому на первом шаге получают диаграмму рассеяния точек, соответствующих объектам, на различных плоскостях.

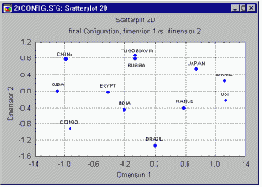
Трехмерные решения также можно проинтерпретировать графически.

Однако эта интерпретация является несколько более сложной.
Заметим, что в дополнение к существенным осям координат, также следует искать кластеры точек, а также те или иные конфигурации точек (окружности, многообразия и др.). Более подробное обсуждение интерпретации полученных конфигураций, см. в работах Borg and Lingoes (1987), Borg and Shye (в печати) или Gutman, (1968).

Использование методов множественной регрессии.
Использование методов множественной регрессии.

Аналитическим способом интерпретации осей координат (описанным в работе Kruskal и Wish, 1978) является применение методов множественной регрессии для регрессирования некоторых имеющих смысл переменных на оси координат. Это легко сделать с помощью модуля Множественная регрессия.

В начало

Приложения

Приложения

"Красота" метода МНШ в том, что вы можете анализировать произвольный тип матрицы расстояний или сходства. Эти сходства могут представлять собой оценки экспертов относительно сходства данных объектов, результаты измерения расстояний в некоторой метрике, процент согласия между судьями по поводу принимаемого решения, количество раз, когда субъект затрудняется различить стимулы и мн.др.

Например, методы МНШ весьма популярны в психологическом исследовании восприятия личности. В этом исследовании анализируются сходства между определенными чертами характера с целью выявления основополагающими личностных качеств (см., например, Rosenberg, 1977). Также они популярны в маркетинговых исследованиях, где их используют для выявления числа и сущности латентных переменных (факторов), например, с целью с целью изучения отношения людей к товарам известных торговых марок (подробнее см. Green и Carmone, 1970).

В общем случае, методы МНШ позволяют исследователю задать клиентам в анкете относительно ненавязчивые вопросы ("насколько похож товар фирмы A на товар фирмы B") и найти латентные переменные для этих анкет незаметно для респондентов.

В начало

Многомерное шкалирование и факторный анализ

Многомерное шкалирование и факторный анализ

Даже несмотря на то, что имеется много сходства в характере исследуемых вопросов, методы МНШ и факторного анализа имеют ряд существенных отличий. Так, факторный анализ требует, чтобы исследуемые данные подчинялись многомерному нормальному распределению, а зависимости были линейными. Методы МНШ не накладывают таких ограничений. Методы МНШ могут быть применимы, пока сохраняет смысл порядок следования рангов сходств. В терминах различий получаемых результатов, факторный анализ стремится извлечь больше факторов (координатных осей или латентных переменных) по сравнению с МНШ; в результате чего МНШ часто приводит к проще интерпретируемым решениям. Однако более существенно то, что методы МНШ можно применять к любым типам расстояний или сходств, тогда как методы ФА требуют, чтобы первоначально была вычислена матрица корреляций. Методы МНШ могут быть основаны на прямом оценивании сходств между стимулами субъектов, тогда как ФА требует, чтобы субъекты были оценены через их стимулы по некоторому списку атрибутов.

Суммируя вышесказанное, можно сказать, что методы МНШ потенциально применимы к более широкому классу исследовательских задач.

В начало

Множественная регрессия

Общее назначение Вычислительные аспекты Метод наименьших квадратов Уравнение регрессии Однозначный прогноз и частная корреляция Предсказанные значения и остатки Остаточная дисперсия и коэффициент детерминации R-квадрат Интерпретация коэффициента множественной корреляции R Предположения, ограничения и обсуждение практических вопросов Предположение линейности Предположение нормальности Ограничения Выбор числа переменных Мультиколлинеарность и плохая обусловленность матрицы Подгонка центрированных полиномиальных моделей Важность анализа остатков

Общее назначение

Общее назначение множественной регрессии (этот термин был впервые использован в работе Пирсона - Pearson, 1908) состоит в анализе связи между несколькими независимыми переменными (называемыми также регрессорами или предикторами) и зависимой переменной. Например, агент по продаже недвижимости мог бы вносить в каждый элемент реестра размер дома (в квадратных футах), число спален, средний доход населения в этом районе в соответствии с данными переписи и субъективную оценку привлекательности дома. Как только эта информация собрана для различных домов, было бы интересно посмотреть, связаны ли и каким образом эти характеристики дома с ценой, по которой он был продан. Например, могло бы оказаться, что число спальных комнат является лучшим предсказывающим фактором (предиктором) для цены продажи дома в некотором специфическом районе, чем "привлекательность" дома (субъективная оценка). Могли бы также обнаружиться и "выбросы", т.е. дома, которые могли бы быть проданы дороже, учитывая их расположение и характеристики.
Специалисты по кадрам обычно используют процедуры множественной регрессии для определения вознаграждения адекватного выполненной работе. Можно определить некоторое количество факторов или параметров, таких, как "размер ответственности" (Resp) или "число подчиненных" (No_Super), которые, как ожидается, оказывают влияние на стоимость работы.
Кадровый аналитик затем проводит исследование размеров окладов (Salary) среди сравнимых компаний на рынке, записывая размер жалования и соответствующие характеристики (т.е. значения параметров) по различным позициям. Эта информация может быть использована при анализе с помощью множественной регрессии для построения регрессионного уравнения в следующем виде:

Salary = .5*Resp + .8*No_Super

Как только эта так называемая линия регрессии определена, аналитик оказывается в состоянии построить график ожидаемой (предсказанной) оплаты труда и реальных обязательств компании по выплате жалования. Таким образом, аналитик может определить, какие позиции недооценены (лежат ниже линии регрессии), какие оплачиваются слишком высоко (лежат выше линии регрессии), а какие оплачены адекватно.

В общественных и естественных науках процедуры множественной регрессии чрезвычайно широко используются в исследованиях. В общем, множественная регрессия позволяет исследователю задать вопрос (и, вероятно, получить ответ) о том, "что является лучшим предиктором для...". Например, исследователь в области образования мог бы пожелать узнать, какие факторы являются лучшими предикторами успешной учебы в средней школе. А психолога мог быть заинтересовать вопрос, какие индивидуальные качества позволяют лучше предсказать степень социальной адаптации индивида. Социологи, вероятно, хотели бы найти те социальные индикаторы, которые лучше других предсказывают результат адаптации новой иммигрантской группы и степень ее слияния с обществом. Заметим, что термин "множественная" указывает на наличие нескольких предикторов или регрессоров, которые используются в модели.

В начало

Вычислительные аспекты
Вычислительные аспекты

Общая вычислительная задача, которую требуется решать при анализе методом множественной регрессии, состоит в подгонке прямой линии к некоторому набору точек.

В простейшем случае, когда имеется одна зависимая и одна независимая переменная, это можно увидеть на диаграмме рассеяния. Метод наименьших квадратов Уравнение регрессии Однозначный прогноз и частная корреляция Предсказанные значения и остатки Остаточная дисперсия и коэффициент детерминации R-квадрат Интерпретация коэффициента множественной корреляции R

Метод наименьших квадратов.
Метод наименьших квадратов.

На диаграмме рассеяния имеется независимая переменная или переменная X и зависимая переменная Y. Эти переменные могут, например, представлять коэффициент IQ (уровень интеллекта, оцененный с помощью теста) и достижения в учебе (средний балл успеваемости - grade point average; GPA) соответственно. Каждая точка на диаграмме представляет данные одного студента, т.е. его соответствующие показатели IQ и GPA. Целью процедур линейной регрессии является подгонка прямой линии по точкам. А именно, программа строит линию регрессии так, чтобы минимизировать квадраты отклонений этой линии от наблюдаемых точек. Поэтому на эту общую процедуру иногда ссылаются как на оценивание по методу наименьших квадратов. (см. также описание оценивания по методу взвешенных наименьших квадратов). Уравнение регрессии.
Уравнение регрессии.

Прямая линия на плоскости (в пространстве двух измерений) задается уравнением Y=a+b*X; более подробно: переменная Y может быть выражена через константу (a) и угловой коэффициент (b), умноженный на переменную X. Константу иногда называют также свободным членом, а угловой коэффициент - регрессионным или B-коэффициентом. Например, значение GPA можно лучше всего предсказать по формуле 1+.02*IQ. Таким образом, зная, что коэффициент IQ у студента равен 130, вы могли бы предсказать его показатель успеваемости GPA, скорее всего, он близок к 3.6 (поскольку 1+.02*130=3.6). Например, анимационный ролик ниже показывает доверительные интервалы (90%, 95% и 99%), построенные для двумерного регрессионного уравнения.

В многомерном случае, когда имеется более одной независимой переменной, линия регрессии не может быть отображена в двумерном пространстве, однако она также может быть легко оценена. Например, если в дополнение к IQ вы имеете другие предикторы успеваемости (например, Мотивация, Самодисциплина), вы можете построить линейное уравнение, содержащее все эти переменные. Тогда, в общем случае, процедуры множественной регрессии будут оценивать параметры линейного уравнения вида:

Y = a + b1*X1 + b2*X2 + ... + bp*Xp

Однозначный прогноз и частная корреляция.
Однозначный прогноз и частная корреляция.

Регрессионные коэффициенты (или B-коэффициенты) представляют независимые вклады каждой независимой переменной в предсказание зависимой переменной. Другими словами, переменная X1, к примеру, коррелирует с переменной Y после учета влияния всех других независимых переменных. Этот тип корреляции упоминается также под названием частной корреляции (этот термин был впервые использован в работе Yule, 1907). Вероятно, следующий пример пояснит это понятие. Кто-то мог бы, вероятно, обнаружить значимую отрицательную корреляцию в популяции между длиной волос и ростом (невысокие люди обладают более длинными волосами). На первый взгляд это может показаться странным; однако, если добавить переменную Пол в уравнение множественной регрессии, эта корреляция, скорее всего, исчезнет. Это произойдет из-за того, что женщины, в среднем, имеют более длинные волосы, чем мужчины; при этом они также в среднем ниже мужчин. Таким образом, после удаления разницы по полу посредством ввода предиктора Пол в уравнение, связь между длиной волос и ростом исчезает, поскольку длина волос не дает какого-либо самостоятельного вклада в предсказание роста помимо того, который она разделяет с переменной Пол. Другими словами, после учета переменной Пол частная корреляция между длиной волос и ростом нулевая. Иными словами, если одна величина коррелирована с другой, то это может быть отражением того факта, что они обе коррелированы с третьей величиной или с совокупностью величин. Предсказанные значения и остатки.
Предсказанные значения и остатки.

Линия регрессии выражает наилучшее предсказание зависимой переменной (Y) по независимым переменным (X). Однако, природа редко (если вообще когда-нибудь) бывает полностью предсказуемой и обычно имеется существенный разброс наблюдаемых точек относительно подогнанной прямой (как это было показано ранее на диаграмме рассеяния). Отклонение отдельной точки от линии регрессии (от предсказанного значения) называется остатком. Остаточная дисперсия и коэффициент детерминации R-квадрат.

Остаточная дисперсия и коэффициент детерминации R-квадрат.

Чем меньше разброс значений остатков около линии регрессии по отношению к общему разбросу значений, тем, очевидно, лучше прогноз. Например, если связь между переменными X и Y отсутствует, то отношение остаточной изменчивости переменной Y к исходной дисперсии равно 1.0. Если X и Y жестко связаны, то остаточная изменчивость отсутствует, и отношение дисперсий будет равно 0.0. В большинстве случаев отношение будет лежать где-то между этими экстремальными значениями, т.е. между 0.0 и 1.0. 1.0 минус это отношение называется R-квадратом или коэффициентом детерминации. Это значение непосредственно интерпретируется следующим образом. Если имеется R-квадрат равный 0.4, то изменчивость значений переменной Y около линии регрессии составляет 1-0.4 от исходной дисперсии; другими словами, 40% от исходной изменчивости могут быть объяснены, а 60% остаточной изменчивости остаются необъясненными. В идеале желательно иметь объяснение если не для всей, то хотя бы для большей части исходной изменчивости. Значение R-квадрата является индикатором степени подгонки модели к данным (значение R-квадрата близкое к 1.0 показывает, что модель объясняет почти всю изменчивость соответствующих переменных). Интерпретация коэффициента множественной корреляции R.
Интерпретация коэффициента множественной корреляции R.

Обычно, степень зависимости двух или более предикторов (независимых переменных или переменных X) с зависимой переменной (Y) выражается с помощью коэффициента множественной корреляции R. По определению он равен корню квадратному из коэффициента детерминации. Это неотрицательная величина, принимающая значения между 0 и 1. Для интерпретации направления связи между переменными смотрят на знаки (плюс или минус) регрессионных коэффициентов или B-коэффициентов. Если B-коэффициент положителен, то связь этой переменной с зависимой переменной положительна (например, чем больше IQ, тем выше средний показатель успеваемости оценки); если B-коэффициент отрицателен, то и связь носит отрицательный характер (например, чем меньше число учащихся в классе, тем выше средние оценки по тестам).

Конечно, если B- коэффициент равен 0, связь между переменными отсутствует.

В начало

Предположения, ограничения и обсуждение практических вопросов
Предположения, ограничения и обсуждение практических вопросов

Предположение линейности Предположение нормальности Ограничения Выбор числа переменных Мультиколлинеарность и плохая обусловленность матрицы Важность анализа остатков

Предположение линейности Предположение нормальности Ограничения Выбор числа переменных Мультиколлинеарность и плохая обусловленность матрицы Важность анализа остатков

Предположение линейности.
Предположение линейности.

Прежде всего, как это видно уже из названия множественной линейной регрессии, предполагается, что связь между переменными является линейной. На практике это предположение, в сущности, никогда не может быть подтверждено; к счастью, процедуры множественного регрессионного анализы в незначительной степени подвержены воздействию малых отклонений от этого предположения. Однако всегда имеет смысл посмотреть на двумерные диаграммы рассеяния переменных, представляющих интерес. Если нелинейность связи очевидна, то можно рассмотреть или преобразования переменных или явно допустить включение нелинейных членов.

Предположение нормальности.
Предположение нормальности.

В множественной регрессии предполагается, что остатки (предсказанные значения минус наблюдаемые) распределены нормально (т.е. подчиняются закону нормального распределения). И снова, хотя большинство тестов (в особенности F-тест) довольно робастны (устойчивы) по отношению к отклонениям от этого предположения, всегда, прежде чем сделать окончательные выводы, стоит рассмотреть распределения представляющих интерес переменных. Вы можете построить гистограммы или нормальные вероятностные графики остатков для визуального анализа их распределения. Ограничения.
Ограничения.

Основное концептуальное ограничение всех методов регрессионного анализа состоит в том, что они позволяют обнаружить только числовые зависимости, а не лежащие в их основе причинные (causal) связи.

Например, можно обнаружить сильную положительную связь (корреляцию) между разрушениями, вызванными пожаром, и числом пожарных, участвующих в борьбе с огнем. Следует ли заключить, что пожарные вызывают разрушения? Конечно, наиболее вероятное объяснение этой корреляции состоит в том, что размер пожара (внешняя переменная, которую забыли включить в исследование) оказывает влияние, как на масштаб разрушений, так и на привлечение определенного числа пожарных (т.е. чем больше пожар, тем большее количество пожарных вызывается на его тушение). Хотя этот пример довольно прозрачен, в реальности при исследовании корреляций альтернативные причинные объяснения часто даже не рассматриваются. Выбор числа переменных.
Выбор числа переменных.

Множественная регрессия - предоставляет пользователю "соблазн" включить в качестве предикторов все переменные, какие только можно, в надежде, что некоторые из них окажутся значимыми. Это происходит из-за того, что извлекается выгода из случайностей, возникающих при простом включении возможно большего числа переменных, рассматриваемых в качестве предикторов другой, представляющей интерес переменной. Эта проблема возникает тогда, когда к тому же и число наблюдений относительно мало. Интуитивно ясно, что едва ли можно делать выводы из анализа вопросника со 100 пунктами на основе ответов 10 респондентов. Большинство авторов советуют использовать, по крайней мере, от 10 до 20 наблюдений (респондентов) на одну переменную, в противном случае оценки регрессионной линии будут, вероятно, очень ненадежными и, скорее всего, невоспроизводимыми для желающих повторить это исследование. Мультиколлинеарность и плохая обусловленность матрицы.
Мультиколлинеарность и плохая обусловленность матрицы.

Проблема мультиколлинеарности является общей для многих методов корреляционного анализа. Представим, что имеется два предиктора (переменные X) для роста субъекта: (1) вес в фунтах и (2) вес в унциях. Очевидно, что иметь оба предиктора совершенно излишне; вес является одной и той же переменной, измеряется он в фунтах или унциях.

Попытка определить, какая из двух мер является лучшим предиктором, выглядит довольно глупо; однако, в точности это происходит при попытке выполнить множественный регрессионный анализ с ростом в качестве зависимой переменной (Y) и двумя мерами веса, как независимыми переменными (X). Если в анализ включено много переменных, то часто не сразу очевидно существование этой проблемы, и она может возникнуть только после того, как некоторые переменные будут уже включены в регрессионное уравнение. Тем не менее, если такая проблема возникает, это означает, что, по крайней мере, одна из зависимых переменных (предикторов) является совершенно лишней при наличии остальных предикторов. Существует довольно много статистических индикаторов избыточности (толерантность, получастное R и др.), а также немало средств для борьбы с избыточностью (например, метод Гребневая регрессия). Подгонка центрированных полиномиальных моделей.
Подгонка центрированных полиномиальных моделей.

Подгонка полиномов высших порядков от независимых переменных с ненулевым средним может создать большие трудности с мультиколлинеарностью. А именно, получаемые полиномы будут сильно коррелированы из-за этого среднего значения первичной независимой переменной. При использовании больших чисел (например, дат в Юлианском исчислении), Эта проблема становится очень серьезной, и если не принять соответствующих мер, то можно прийти к неверным результатам. Решением в данном случае является процедура центрирования независимой переменной, т.е. вначале вычесть из переменной среднее, а затем вычислять многочлены. Более подробное обсуждение этого вопроса (и анализа полиномиальных моделей в целом) смотрите, например, в классической работе Neter, Wasserman & Kutner (1985, глава 9). Важность анализа остатков.
Важность анализа остатков.

Хотя большинство предположений множественной регрессии нельзя в точности проверить, исследователь может обнаружить отклонения от этих предположений. В частности, выбросы (т.е. экстремальные наблюдения) могут вызвать серьезное смещение оценок, "сдвигая" линию регрессии в определенном направлении и тем самым, вызывая смещение регрессионных коэффициентов.Часто исключение всего одного экстремального наблюдения приводит к совершенно другому результату.

В начало

Моделирование структурными уравнениями

Обзор основных понятий Идеи, лежащие в основе структурного моделирования Моделирование структурными уравнениями и диаграммы путей

Обзор основных понятий
Обзор основных понятий

Наметившийся в последнее время прогресс в области многомерного статистического анализа и анализа корреляционных структур, объединенный с новейшими вычислительными алгоритмами, послужил отправной точкой для создания новой, но уже получившей признание, техники Моделирования структурными уравнениями. Эта, по сути дела, всеобъемлющая и необычайно мощная техника многомерного анализа включает большое количество методов из различных областей статистики. Кратко можно сказать, что SEPATH представляет собой мощное развитие многих методов многомерного анализа, а именно множественная регрессия и факторный анализ получили здесь естественное развитие и объединение. Далее в этой главе мы будем предполагать, что читатель уже знаком с основными статистическими понятиями, которые описаны в разделе Элементарные понятия статистики, в том числе с понятием дисперсии, ковариации и корреляции. Если вам кажется, что ваших знаний не достаточно для дальнейшего чтения, мы рекомендуем просмотреть раздел Основные статистики и таблицы, чтобы восполнить эти пробелы. Хотя это и не является обязательным, нам было бы проще объяснить вам возможности структурного моделирования, если бы предварительно вы получили некоторое представление о методах факторного анализа.

Основные задачи, для решения которых используются структурные уравнения следующие: Причинное моделирование или анализ путей, при проведении которого предполагается, что между переменными имеются причинные взаимосвязи. Возможна проверка гипотез и подгонка параметров причинной модели, описываемой линейными уравнениями. Причинные модели могут включать явные или латентные переменные, или и те и другие; Подтверждающий факторный анализ, используемый как развитие обычного факторного анализа для проверки определенных гипотез о структуре факторных нагрузок и корреляций между факторами; Факторный анализ второго порядка, являющийся модификацией факторного анализа, при проведении которого для получения факторов второго порядка анализируется корреляционная матрица общих факторов; Регрессионные модели, являющиеся модификацией Многомерного линейного регрессионного анализа, в котором коэффициенты регрессии могут быть зафиксированы равными друг другу или каким-нибудь заданным значениям; Моделирование ковариационной структуры, которое позволяет проверить гипотезу о том, что матрица ковариации имеет определенный вид.
Например, с помощью этой процедуры вы можете проверить гипотезу о равенстве дисперсий у всех переменных; Модели корреляционной структуры, которое позволяет проверить гипотезу о том, что матрица корреляции имеет определенный вид. Классическим примером является гипотеза о том, что матрица корреляции имеет циклическую структуру (см. книгу Guttman, 1954; Wiggins, Steiger, и Gaelick, 1981); Модели структуры средних, которые позволяют исследовать структуру средних, например, одновременно с анализом дисперсий и ковариаций. Многие виды моделей попадают сразу в несколько из этих категорий, поэтому при практическом анализе структурной модели не так-то просто ее классифицировать, да в этом и нет особой необходимости.

Структурные уравнения, включающие только линейные связи между явными и латентными переменными, могут быть изображены в виде диаграмм путей. Поэтому даже начинающий пользователь может провести сложный анализ с минимальными затратами времени на обучение.

В начало

Идеи, лежащие в основе структурного моделирования

Идеи, лежащие в основе структурного моделирования

Одной из основных используемых идей, с которой знакомятся все начинающие изучение статистики, является эффект воздействия аддитивных и мультипликативных преобразований. Как учат студентов, если умножить каждое число на некоторую константу K, среднее значение также умножиться на K. При этом стандартное отклонение умножится на модуль K.

Например, рассмотрим набор из трех чисел 1, 2, 3. Эти числа имеют среднее равное 2 и стандартное отклонение равное 1. Далее, пусть мы умножили все три числа на 4. Тогда среднее значение будет равно 8, стандартное отклонение примет значение 4, а дисперсия будет равна 16.

Таким образом, если мы имеем набор чисел X связанные с другим набором чисел Y зависимостью Y = 4X, то дисперсия Y должна быть в16 раз больше, чем дисперсия X. Поэтому мы можем проверить гипотезу о том, что Y и X связаны уравнением Y = 4X, косвенно - сравнением дисперсий переменных Y и X.

Эта идея может быть различными способами обобщена на несколько переменных, связанных системой линейных уравнений.

При этом правила преобразований становятся более громоздкими, вычисления более сложными, но основной смысл остается прежним - вы можете проверить связаны ли переменные линейной зависимостью, изучая их дисперсии и ковариации.

Для проверки имеет ли ковариационная матрица заданную структуру статистики используют несколько процедур. Процесс структурного моделирования состоит из следующих этапов: вы описываете (обычно с помощью диаграммы путей) модель, представляющую ваше понимание зависимостей между переменными; программа определяет, с помощью специальных внутренних методов, какие значения дисперсий и ковариаций переменных получаются в текущей модели на основании входных данных; программа проверяет, насколько хорошо полученные дисперсии и ковариации удовлетворяют нашей модели; программа сообщает пользователю полученные результаты статистических испытаний, а также выводит оценки параметров и стандартные ошибки для численных коэффициентов в линейных уравнениях вмести с большим количеством дополнительной диагностической информации; на основании этой информации, вы решаете, хорошо ли текущая модель согласуется с вашими данными. Основные этапы процесса структурного моделирования описаны далее в тексте и показаны на диаграмме внизу. Во-первых, хотя логика математических вычислений при проведении структурного моделирования очень сложная, основные этапы соответствуют пяти шагам на диаграмме.

Во-вторых, следует помнить, что не разумно ожидать идеального соответствия модели и данных - по нескольким причинам. Структурные модели с линейными зависимостями являются только приближениями реальных явлений. Природные зависимости далеки от линейных. Поэтому, истинные зависимости между переменными, скорее всего, не линейны. Более того, истинность многих статистических предположений, накладываемых на проверяемую модель, остается под большим вопросом. На практике нас интересует не то "Идеально ли модель согласуется с данными?" а, "Согласуется ли она достаточно хорошо, чтобы быть полезной для практического использования и разумного объяснения структуры наблюдаемых данных?"

В-третьих, следует помнить, что идеальное соответствие модели данным не обязательно означает, что модель верна. Мы вообще не можем доказать, что модель верна - умение доказывать правильность модели эквивалентно умению предсказывать будующее. Например, вы можете сказать "Если Джо - кошка, то у Джо есть усы". Однако, из того, что "У Джо есть усы" не следует, что Джо - кошка. Аналогично, вы можете сказать, что "если определенная причинная модель верна, то она согласуется с наблюдаемыми данными". Однако, модель, согласующаяся с данными, не обязательно является верной. Возможно, существует другая модель, которая ничуть не хуже согласуется с теми же данными.

В начало

Моделирование структурными уравнениями и диаграммы путей

Моделирование структурными уравнениями и диаграммы путей

Диаграммы путей играют существенную роль в процессе структурного моделирования. Диаграммы путей напоминают используемые блок-схемы. Они изображают переменные, связанные линиями, которые используются для отображения причинных связей. Каждая связь или путь включает в себя две переменные (заключенные в прямоугольник или овал), соединенные стрелками (линиями, обычно прямыми, имеющими стрелку-указатель на одном конце) или дугами (линиями, обычно искривленными, без стрелок указателей).
Путевые диаграммы удобнее всего представлять в качестве инструмента для указания, какие переменные вызывают изменения в других переменных. Однако этого описание не является абсолютно точным. Можно дать более точное описание.

Рассмотрим классическое линейное регрессионное уравнение

Y = aX + e

И его представление в виде пути, показанное ниже.

Такие диаграммы устанавливают простое взаимно-однозначное отображение, сохраняющее структуру модели, также называемое изоморфизмом. Все переменные в системе уравнений размещаются на диаграмме в прямоугольниках или овалах. Каждое уравнение отображается на диаграмме следующим путем: все независимые переменные (переменные в правой части уравнения) имеют стрелки, указывающие на независимые переменные.

Весовые коэффициенты располагаются вблизи от соответствующих стрелок. Диаграмма снизу содержит представление системы простых линейных уравнений в виде диаграммы путей.

Отметим, что кроме представления линейных зависимостей в виде стрелок, диаграмма также содержит некоторые другие выражения. Во-первых, дисперсия независимых переменных, которая должна быть задана для проверки модели структурных связей, показаны на диаграмме с использованием изогнутых линий без стрелок. Такие линии мы называем дугами. Во-вторых, некоторые переменные, изображены в овальных, а не в прямоугольных рамках. Явные переменные (т.е., переменные, которые можно измерить непосредственно) на диаграммах изображаются внутри прямоугольников. Латентные переменные (т.е., которые нельзя непосредственно измерить, как, например, факторы в факторном анализе, или остатки в регрессионном) изображаются внутри овалов или окружностей. Например, переменная E на диаграмме сверху может рассматриваться как остаток линейной регрессии, когда значение Y предсказывается по значению X. Такие остатки не наблюдаются непосредственно, но в принципе могут быть вычислены по известным значениям Y и X (если a известно), поэтому они называются латентными (скрытыми) переменными и помещаются внутри овалов.

Мы рассмотрели очень простой пример диаграммы путей. В общем случае, мы заинтересованы в проверке намного более сложных моделей. Если же система уравнений становится слишком сложной, исследователи обычно переходят к рассмотрению ковариационных структур. В конце концов, модели становится настолько сложной и запутанной, что они перестают понимать ее основные принципы. Но есть доводы, которые говорят о том, что навыки проверки причинных моделей слабо связаны с проверкой линейных моделей. Переменные могут быть связаны нелинейно. Они могут быть линейно связаны по причинам, не относящимся к тому, что мы выбрали в качестве причины в нашей модели. Древнее изречение "наблюдаемая зависимость не означает причинной зависимости" остается верным, даже для сложной и многомерной корреляции.

То, что причинное моделирование действительно позволяет исследовать, это насколько данные отличаются от соответствующих выводов причинной модели (а именно, от предполагаемой ковариационной структуры). Если система линейных уравнений, изоморфная диаграмме путей, хорошо согласуется с данными, это позволяет оставить модель для дальнейшего анализа или использования, но не доказывает ее истинность.

Хотя диаграммы путей могут использоваться для отражения причинных связей в наборе переменных, они не предполагают реального наличия таких связей. Диаграммы путей часто используются для простого и изоморфного представления системы линейных уравнений. По этому, они могут выражать линейные связи вне зависимости от того, имеются ли на самом деле описанные причинные связи. Следовательно, хотя мы интерпретируем диаграмму на рисунке сверху как "X влияет на Y", диаграмма также может обозначать графическое представление линейного регрессионного соотношения между X и Y.

В начало

Надежность и позиционный анализ

Основная цель Основные идеи Классическая модель проверки Надежность Суммарные шкалы Альфа Кронбаха Split-half надежность Поправка на затухание Построение надежной шкалы

Этот обзор обсуждает понятие надежности измерений, которое используется в социальных науках (но не в исследованиях промышленной статистики или медицины). Термин надежность, используемый в промышленной статистике, обозначает функцию ошибок (как функцию времени). Для обсуждения термина надежность в применении к качеству продукта (т.е. в промышленной статистике) обратитесь к разделу Анализ надежности/времен отказов в главе Анализ процессов (см. также раздел Повторяемость и воспроизводимость в той же главе и главу Анализ выживаемости/времен отказов). Для сравнения этих (очень разных) понятий надежности, см. Надежность.
Основная цель Основные идеи Классическая модель проверки Надежность Суммарные шкалы Альфа Кронбаха Split-half надежность Поправка на затухание Построение надежной шкалы

Основная цель

Во многих областях исследований точное измерение переменных само по себе представляет сложную задачу. Например, в психологии точное измерение личностных характеристик или отношений к чему-либо - необходимый первый шаг, предваряющий всякую теорию. В целом, очевидно, что во всех социальных дисциплинах ненадежные измерения будут препятствовать попытке предсказать поведение людей.
В прикладных исследованиях, когда наблюдения над переменными затруднены, также важна точность измерений. Например, надежное измерение производительности служащих, как правило, является сложной задачей. Однако очевидно, что эти измерения необходимы для любой системы оплаты, основанной на производительности труда.

Модуль Надежность и позиционный анализ позволит вам построить надежные шкалы, а также улучшить используемые шкалы. Модуль Надежность и позиционный анализ поможет вам также при конструировании и оценивании суммарных шкал, т.е. шкал, которые используются при многократных индивидуальных измерениях (различные позиции или вопросы, повторяющиеся измерения и т.д.). Программа вычисляет многочисленные статистики, позволяющие оценить надежность шкалы с помощью классической теории тестирования.

Оценивание надежности шкалы основано на корреляциях между индивидуальными позициями или измерениями, составляющими шкалу, и дисперсиями этих позиций. Если вы не знакомы с коэффициентом корреляции или дисперсией, обратитесь к соответствующим разделам главы Основные статистики и таблицы.

Классическая теория тестирования имеет долгую историю, и существует много пособий по этому предмету. Для подробного знакомства можно рекомендовать, например, Carmines and Zeller (1980), De Gruitjer and Van Der Kamp (1976), Kline (1979, 1986) или Thorndyke and Hagen (1977). Широко известной, "классической" монографией является книга Nunally (1970), в которой хорошо освещено тестирование в области психологии и образования.

Проверка гипотез о зависимости позиций.
Проверка гипотез о зависимости позиций.

STATISTICA включает в себя процедуру моделирования структурными уравнениями (SEPATH), где можно проверить специальные гипотезы о связи между множествами позиций или различных критериев (например, гипотезу, что два множества позиций измеряют одну и ту же структуру, анализируют матрицы изменчивости используемого метода и т.д.).

В начало

Основные идеи
Основные идеи

Предположим, вы хотите построить анкету, чтобы измерить степень предубеждения людей против машин иностранного производства.

Как это сделать? Вы могли бы начать, например, с формулировки следующих утверждений: "Машинам иностранного производства не хватает индивидуальности", "Машины иностранного производства выглядят одинаково" и т.д. Затем вы можете предложить эти пункты группе субъектов, (например, группе людей, которые никогда не были владельцами машин иностранного производства). Респондентам предлагалось бы указать степень своего согласия с этими утверждениями по 9-балльной шкале, имеющей градации от 1=не согласен до 9=согласен.

Истинные значения и погрешности.
Истинные значения и погрешности.

Рассмотрим подробнее, что подразумевается под точным измерением в этом примере. Гипотеза состоит в том, что в сознании людей существует такой объект (теоретическая конструкция) как "предубеждение против машин иностранного производства" и каждый пункт анкеты (иными словами, позиция анкеты) в какой-то степени "раскрывает" эту концепцию. Вы можете сказать, что ответ очередного человека на определенную позицию анкеты включает два аспекта: во-первых, отражает предубеждение против машин иностранного производства, во-вторых, отражает некоторый скрытый, неконтролируемый фактор, соответствующий данной позиции. Например, рассмотрим утверждение: "Все машины иностранного производства выглядят одинаково". Согласие или несогласие субъекта с этим утверждением будет частично зависеть от некоторых других аспектов вопроса или самого респондента. Например, у респондента есть друг, который только что купил машину иностранного производства необычного вида и этот фактор влияет на степень согласия с приведенным утверждением.

Проверка гипотез о зависимости между позициями и критериями.
Проверка гипотез о зависимости между позициями и критериями.

Для проверки специальных гипотез о связи между множествами позиций или различных критериев (критерий того, что два множества позиций измеряют одну и ту же структуру, анализируют матрицы изменчивости используемого метода и т.д.) используйте процедуру Моделирования структурными уравненями (SEPATH).

.

В начало

Классическая модель проверки
Классическая модель проверки

Каждое измерение (ответ на вопрос) включает в себя как истинное значение (предубеждение против машин иностранного производства), так и частично неконтролируемую, случайную погрешность. Это можно описать следующим классическим уравнением:
X = тау + ошибка
В данном уравнении X выражает соответствующее реальное измерение, т.е. ответ (отклик) субъекта на вопрос анкеты; тау обычно используется для обозначения неизвестного истинного значения или истинной метки, ошибка обозначает погрешность измерения.

В начало

Надежность
Надежность

В этом контексте надежность понимается непосредственно: измерение является надежным, если его основную часть, по отношению к погрешности, составляет истинное значение. Например, позиция анкеты: "Красные машины иностранного производства особенно уродливы", скорее всего, даст ненадежное измерение для предубеждения против иностранных машин. Это происходит потому, что, вероятно, у людей существуют значительные различия, касающиеся цветовых симпатий и антипатий. Таким образом, позиция будет учитывать не только предубеждение против иностранных машин, но также цветовое предпочтение субъектов. Поэтому в ответе на данную позицию доля истинной метки (истинного предубеждения) будет относительно мала (будет большой ошибка).

Меры надежности.
Меры надежности.

Отсюда нетрудно вывести критерий или статистику для описания надежности позиции или шкалы. Именно, можно ввести индекс надежности, как отношение вариации истинной метки (истинного значения), присущей субъектам или респондентам, к общей вариации:

Надежность =

2(истинная метка) /

2(всего наблюдений)

В начало

Суммарные шкалы
Суммарные шкалы

Зададимся теперь вопросом: что произойдет, если просуммировать несколько более или менее надежных позиций, построенных с целью оценки предубеждения против иностранных машин? Предположим, что вопросы были сформулированы так, чтобы охватить возможно более широкий спектр различных предубеждений против машин иностранного производства.

Если ошибочная компонента в ответах респондентов на каждый вопрос действительно случайна, то можно ожидать, что в ответах на различные вопросы случайные компоненты будут взаимно подавлять друг друга. Математическое ожидание суммарной погрешности по совокупности всех вопросов (позиций шкалы) будет равно нулю. Компонента истинной метки остается неизменной при суммировании по всем позициям. Следовательно, чем больше будет добавлено вопросов, тем точнее истинная метка (по отношению к погрешности) будет отражена на суммарной шкале.

Количество позиций и надежность.
Количество позиций и надежность.

Это заключение описывает важный принцип построения критерия, а именно: чем больше позиций участвуют в построении шкалы для измерения данной концепции, тем более надежным будет измерение (суммарная шкала). Может быть, следующий пример лучше пояснит это. Предположим, вы хотите измерить рост 10 людей, используя только простую палочку или, например, свой локоть как измерительное устройство. В этом примере нас интересует не абсолютная точность измерений (в дюймах или сантиметрах), а возможность верно различать 10 индивидуумов по результатам измерений. Если, прикладывая палочку, вы измерите каждого человека только один раз, то результат может и не быть очень надежным. Однако если вы измерите каждого субъекта 100 раз и затем возьмете среднее этих 100 измерений как итоговый результат для соответствующего роста участника, то будете в состоянии очень точно и надежно различать людей (основываясь единственно на простой измерительной палочке, а не на линейке).

Теперь обратимся к некоторым статистикам, которые используются для оценивания надежности суммарной шкалы.

В начало

Альфа Кронбаха
Альфа Кронбаха

Вернемся к примеру с предубеждениями. Если есть несколько субъектов, отвечающих на вопросы, то можно вычислить дисперсию для каждого вопроса и суммарной шкалы. Дисперсия для суммарной шкалы будет меньше, чем сумма дисперсий каждого отдельного вопроса в том случае, когда вопрос измеряет (оценивает) одну и ту же изменчивость между субъектами, т.е.

если они измеряют некоторую истинную метку. Математически дисперсия суммы двух вопросов равна сумме двух дисперсий минус удвоенная ковариация, т.е. равна величине истинной дисперсии метки, общей для двух вопросов.

Вы можете оценивать долю дисперсии истинной метки, покрываемую вопросами, путем сравнения суммы дисперсий отдельных вопросов с дисперсией суммарной шкалы. Конкретно, вы можете вычислить величину:

= (k/(k-1)) * [1-

(s2i)/s2сум]

Это формула для общепринятого индекса надежности, так называемого коэффициента - альфа Кронбаха (

). В этой формуле si**2 обозначают дисперсии для k отдельных позиций; sсум**2 - дисперсию для суммы всех позиций. Если не существует истинной метки, а только случайная погрешность в ответах на вопросы (являющаяся неконтролируемой и единственной, а следовательно, некоррелированной между субъектами), то дисперсия суммы будет такой же, как сумма дисперсий отдельных позиций. Поэтому коэффициент альфа будет равен нулю. Если все вопросы совершенно надежны и измеряют один и тот же объект (истинную метку), то коэффициент альфа равен 1. (1-

(si**2)/sсум**2 равен (k-1)/k; умножив на k/(k-1), получим 1.)

Альтернативная терминология.
Альтернативная терминология.

Альфа Кронбаха, вычисленная для дихотомий или переменных, принимающих только два значения (например, для ответов истинно/ложно), идентична так называемой формуле Кьюдера-Ричардсона-20 для надежности суммарных шкал. И в том, и в другом случае, поскольку надежность реально вычисляется, исходя из непротиворечивости всех вопросов в суммарной шкале, коэффициент надежности, вычисленный таким образом, также относится к внутренне непротиворечивой надежности.

В начало

Split-half надежность
Split-half надежность

Другим способом вычисления надежности суммарной шкалы является разбиение суммарной шкалы случайным образом на две половины [этот прием, называемый по-английски split-half, часто используется в медицине и биологии для оценки надежности результатов; разбиение производится случайным образом, что позволяет избежать искусственных эффектов].

Если суммарная шкала совершенно надежна, то следует ожидать, что обе части абсолютно коррелированы (т.е. r = 1.0). Если суммарная шкала не является абсолютно надежной, то коэффициент корреляции будет меньше 1. Можно оценить надежность суммарной шкалы посредством split-half коэффициента Спирмена-Брауна:

rсб = 2rxy /(1+rxy)

В этой формуле rсб - это коэффициент split-half надежности, а rxy является корреляцией между двумя половинами шкалы.

В начало

Поправка на затухание
Поправка на затухание

Рассмотрим теперь некоторые последствия, к которым приводит не абсолютная надежность. Предположим, что вы измеряете предубеждения против машин иностранного производства для прогнозирования каких-либо других показателей таких, например, будущего спроса на эти машины. Если ваша шкала коррелирует с таким показателем, то этот факт повысит вашу уверенность в достоверности шкалы, т.е. в том, что она действительно измеряет предубеждение против иномарок, а не что-нибудь вовсе другое. Построение достоверной выборки - это продолжительный процесс, при котором исследователь изменяет шкалу в соответствии с различными внешними критериями, теоретически связанными с той концепцией, для подтверждения которой строится шкала.

Как будет влиять на достоверность шкалы тот факт, что шкала не абсолютно надежна? Маловероятно, чтобы часть шкалы, включающая случайную ошибку, коррелировала с некоторым внешним показателем. Поэтому, если пропорция истинной метки (истинного значения) в шкале равна 60% (т.е. надежность равна лишь 0,60), то корреляция между шкалой и внешним показателем будет затухать; т.е. будет ослаблена. Это означает, что она будет меньше, чем фактическая корреляция между двумя истинными метками (т.е. между показателем, измеряемым шкалой, и другим, внешним по отношению к шкале показателем). Фактически достоверность шкалы всегда ограничивается ее надежностью.

При заданной надежности двух, связанных между собой измерений (т.е. шкалы и другого исследуемого показателя), можно оценить корреляцию между истинными значениями при обоих измерениях.

Иными словами, вы можете изменить корреляцию следующим образом - ввести так называемую поправку на затухание:

rxy,коррект = rxy /(rxx*ryy)

В этой формуле rxy,коррект обозначает скорректированный или поправленный коэффициент корреляции. Иными словами, это оценка корреляции между истинными метками при двух измерениях x и y. Коэффициент rxy обозначает непоправленную корреляцию, а rxx и ryy обозначают надежности измерений (шкал) x и y. Модуль Надежность и позиционный анализ предоставляет опцию для вычисления корреляции с поправкой на "затухание". Это изменение корреляции обусловлено либо значениями, задаваемыми пользователем, либо реальными исходными данными (в последнем случае надежности двух измерений оцениваются, исходя из данных).

В начало

Построение надежной шкалы
Построение надежной шкалы

После нашего обсуждения, по-видимому, понятно, что шкала тем лучше (т.е. тем достоверней), чем она надежнее. Как отмечалось ранее, один из способов сделать шкалу более достоверной - просто добавить в нее новые позиции. Модуль Надежность и позиционный анализ включает в себя опцию, позволяющую вычислить, сколько еще позиций (вопросов) необходимо добавить, чтобы получить заданную надежность, или как изменится надежность шкалы при добавлении некоторого количества новых позиций. Однако на практике количество позиций в шкале ограничивается различными факторами (например, респонденты устали и просто не будут отвечать на большое число вопросов, полное пространство ограничено и т.д.). Теперь, возвращаясь к примеру с предубеждениями, перечислим шаги, которые в общем случае нужны для построения надежной шкалы:

Шаг 1: Формулирование вопросов.
Шаг 1: Формулирование вопросов.

Первый шаг - написать вопросы. Это исключительно творческий процесс, когда исследователь создает как можно больше вопросов, которые, как ему кажется, всесторонне описывают предубеждение против машин иностранного производства. Теоретически следует выбирать вопросы, связанные с определяемой концепцией.

На практике, например, в маркетинговых исследованиях, часто используют фокусные группы для того, чтобы осветить столь много аспектов, сколь это возможно. Например, можно попросить небольшую группу активно заинтересованных американских автомобильных потребителей выразить свое отношение к машинам иностранного производства. В области образовательного и психологического тестирования на этой стадии конструирования шкалы обычно обращают внимание на аналогичные анкеты для того, чтобы получить максимально полное представление концепции.

Шаг 2: Выбор вопросов оптимальной трудности.
Шаг 2: Выбор вопросов оптимальной трудности.

В первый вариант вашего вопросника о "предпочтениях" включайте как можно больше вопросов. Теперь предложите эту анкету начальной выборке типичных респондентов и проанализируйте результаты по каждому пункту. Во-первых, вы увидите различные характеристики вопросов и выделите эффект пол-потолок. Если все согласны или не согласны с вопросом, то он, очевидно, не поможет провести различия между респондентами и окажется бесполезным для построения надежной шкалы. В конструкции теста долю респондентов, которые согласны или не согласны с вопросом, или долю тех, кто "верно" отвечают на вопросы (т.е. угадывают реально существующую тенденцию) называют трудностью вопроса. В сущности, вы могли бы посмотреть на выборочные средние и стандартные отклонения для вопросов и удалить те из них, которые дают резко выделяющиеся средние и нулевые или близкие к нулю дисперсии.

Шаг 3: Выбор внутренне непротиворечивых вопросов.
Шаг 3: Выбор внутренне непротиворечивых вопросов.

Напомним, что надежная шкала состоит из вопросов (позиций), которые пропорционально измеряют истинную метку; в нашем примере нам желательно отобрать вопросы, которые главным образом измеряют предубеждение против иностранных машин, при этом накладываются некоторые скрытые факторы, являющиеся случайными погрешностями. Для иллюстрации посмотрим на таблицу:

STATISTICA
АНАЛИЗ
НАДЕЖНОСТИ Итоги для шкалы: Среднее=46.1100 Ст.откл.=8.26444 N набл:100
Альфа Кронбаха: .794313 Стандартизованная альфа: .800491
Средняя межпозиционная корреляция: .297818
Переменная Среднее
при удал. Дисперсия
при удал. Ст.откл.
при удал. Общ-поз.
коррел. Квадрат
мн. регр. Альфа
при удал. ITEM1
ITEM2
ITEM3
ITEM4
ITEM5
ITEM6
ITEM7
ITEM8
ITEM9
ITEM10

41.61000
41.37000
41.41000
41.63000
41.52000
41.56000
41.46000
41.33000
41.44000
41.66000

51.93790
53.79310
54.86190
56.57310
64.16961
62.68640
54.02840
53.32110
55.06640
53.78440

7.206795
7.334378
7.406882
7.521509
8.010593
7.917474
7.350401
7.302130
7.420674
7.333785

.656298
.666111
.549226
.470852
.054609
.118561
.587637
.609204
.502529
.572875

.507160
.533015
.363895
.305573
.057399
.045653
.443563
.446298
.328149
.410561

.752243
.754692
.766778
.776015
.824907
.817907
.762033
.758992
.772013
.763314

В ней приведены 10 вопросов. Наибольший интерес представляют три крайних правых столбца таблицы. Они показывают корреляцию между соответствующим вопросом и общей суммарной шкалой (без соответствующего вопроса), квадрат корреляции между соответствующим вопросом и другими вопросами и внутреннюю непротиворечивость шкалы (коэффициент альфа), если соответствующий вопрос будет удален. Очевидно, вопросы 5 и 6 резко выделяются в силу того, что они не согласуются с остальной частью шкалы. Их корреляции с суммарной шкалой равны 0.05 и 0.1 соответственно, в то время как все другие коррелируют с показателем 0.45 или лучше. В крайнем правом столбце можно увидеть, что надежность шкалы будет около 0.82, если удалить любой из этих двух вопросов. Очевидно, эти два вопроса следует убрать из шкалы.

Шаг 4: Возвращаемся к шагу 1.
Шаг 4: Возвращаемся к шагу 1.

После удаления всех вопросов, которые не согласуются со шкалой, вы можете остаться без достаточного количества вопросов для того, чтобы создать полностью надежную шкалу (напомним, что чем меньше вопросов, тем менее надежная шкала). На практике исследователь часто несколько раз проходит через этапы создания и удаления вопросов до тех пор, пока не придет к окончательному набору вопросов, образующих надежную шкалу.

Тетрахорическая корреляция.
Тетрахорическая корреляция.

В образовательных и психологических тестах обычно используют вопросы с ответами типа да/нет. В этом случае альтернативой к обычному коэффициенту корреляции является коэффициент тетрахорической корреляции. Обычно коэффициент тетрахорической корреляции больше, чем стандартный коэффициент корреляции; поэтому Nunally (1970, стр. 102) не рекомендует его использовать при оценивании надежности. Однако до сих пор этот коэффициент используется на практике (например, при математическом моделировании).

В начало