Анализ процессов

Анализ производственных процессов

Выборочные планы Основное назначение Методы вычислений Средние для гипотез Н0 и Н1 Вероятности ошибок альфа и бета Планы с фиксированным объемом выборки Последовательные выборочные планы Выводы Анализ пригодности процессов Введение Методы вычислений

Индексы (показатели) пригодности Качество и пригодность процесса Использование экспериментов для повышения пригодности Проверка предположения о нормальности распределения Доверительные границы Повторяемость и воспроизводимость измерений Введение Методы вычислений Графики повторяемости и воспроизводимости Компоненты дисперсии Выводы Негауссовские распределения Введение Подгонка методом моментов Качество подгонки: графики квантилей и вероятностей Негауссовские индексы пригодности (метод процентилей) Анализ Вейбулла, надежность и времена отказов Основные задачи Распределение Вейбулла Цензурированные наблюдения Двух- и трехпараметрическое распределение Вейбулла Оценка параметров Критерии согласия Интерпретация результатов Группированные данные Изменения порядка времен отказов для многократно цензурированных данных Функция распределения Вейбулла, надежность и функции риска

Планы выборочного контроля подробно обсуждаются в работах Duncan (1974) и Montgomery (1991). Большинство процедур оценивания пригодности процессов (и соответствующих показателей) были сравнительно недавно заимствованы из Японии и внедрены в США (Kane, 1986); они обсуждаются в трех превосходных практических руководствах Bohte (1988), Hart and Hart (1989) и Pyzdek (1989); подробные обсуждения этих методов можно также найти в работе Montgomery (1991).
Выборочные планы Основное назначение Методы вычислений Средние для гипотез Н0 и Н1 Вероятности ошибок альфа и бета Планы с фиксированным объемом выборки Последовательные выборочные планы Выводы Анализ пригодности процессов Введение Методы вычислений Индексы (показатели) пригодности Качество и пригодность процесса Использование экспериментов для повышения пригодности Проверка предположения о нормальности распределения Доверительные границы Повторяемость и воспроизводимость измерений Введение Методы вычислений Графики повторяемости и воспроизводимости Компоненты дисперсии Выводы Негауссовские распределения Введение Подгонка методом моментов Качество подгонки: графики квантилей и вероятностей Негауссовские индексы пригодности (метод процентилей) Анализ Вейбулла, надежность и времена отказов Основные задачи Распределение Вейбулла Цензурированные наблюдения Двух- и трехпараметрическое распределение Вейбулла Оценка параметров Критерии согласия Интерпретация результатов Группированные данные Изменения порядка времен отказов для многократно цензурированных данных Функция распределения Вейбулла, надежность и функции риска

Планы выборочного контроля подробно обсуждаются в работах Duncan (1974) и Montgomery (1991).
Большинство процедур оценивания пригодности процессов (и соответствующих показателей) были сравнительно недавно заимствованы из Японии и внедрены в США (Kane, 1986); они обсуждаются в трех превосходных практических руководствах Bohte (1988), Hart and Hart (1989) и Pyzdek (1989); подробные обсуждения этих методов можно также найти в работе Montgomery (1991).

Подробные инструкции по вычислению и интерпретации показателей пригодности даются также в издании Fundamental Statistical Process Control Reference Manual, опубликованном ASQC (Аmerican Society for Quality Control) и AIAG (Automotive Industry Action Group, 1991; далее это руководство упоминается как ASQC/AIAG, 1991). Методы повторяемости и воспроизводимости (R & R) обсуждаются в работах Grant and Leavenworth (1980), Pyzdek (1989), а также в Montgomery (1991); более подробное обсуждение этой темы (оценивание дисперсии) приводится также в работе Duncan (1974).

Подробные инструкции по проведению и анализу экспериментов по повторяемости и воспроизводимости (R & R) содержатся в руководстве Measurement Systems Analysis Reference Manual, опубликованном ASQC/AIAG (1990). Краткое описание этих процедур можно найти в следующих разделах. Дополнительные сведения об анализе планов со случайными эффектами и оценке компонент дисперсии можно найти в разделе Компоненты дисперсии.

Планы выборочного контроля Основное назначение Методы вычислений Средние для гипотез H0 и H1 Вероятности ошибок альфа и бета Планы с фиксированным объемом выборки Последовательные выборочные планы Выводы
Основное назначение Методы вычислений Средние для гипотез H0 и H1 Вероятности ошибок альфа и бета Планы с фиксированным объемом выборки Последовательные выборочные планы Выводы

Основное назначение
Основное назначение

Общая проблема, с которой сталкиваются инженеры по контролю качества, состоит в том, чтобы определить, сколько изделий из партии (например, полученной от поставщика) необходимо исследовать, чтобы быть уверенными в том, что изделия этой партии обладают приемлемым качеством.


Допустим, что у вашей автомобильной компании есть поставщик поршневых колец для небольших двигателей, и ваша цель – разработать процедуру выборочного контроля поршневых колец в присылаемых партиях, обеспечивающую требуемое качество. В принципе эта проблема сходна с проблемой, рассмотренной в разделе Контроль качества, где обсуждаются вопросы статистического контроля качества промышленной продукции.

Выборочный контроль при приемке.
Выборочный контроль при приемке.

Процедуры выборочного контроля применяются в том случае, когда нужно решить, удовлетворяет ли определенным спецификациям партия изделий, не изучая при этом все изделия. В силу природы проблемы – принимать или не принимать партию изделий – эти методы иногда называют статистическим приемочным контролем (acceptance sampling)

Преимущества над полным контролем.
Преимущества над полным контролем.

Очевидное преимущество выборочного контроля над полным (сплошным) контролем партии состоит в том, что изучение только выборки (а не всей партии) требует меньшего времени и финансовых затрат. В некоторых случаях исследование изделия является разрушающим (например, испытание стали на предельную прочность), и сплошной контроль уничтожил бы всю партию. Наконец, с точки зрения управления производством, отбраковка всей партии или поставки от данного поставщика (на основании выборочного контроля) вместо браковки лишь определенного процента дефектных изделий (на основании сплошного контроля) часто заставляет поставщиков строже придерживаться стандартов качества.

Методы вычислений
Методы вычислений

В принципе вычислительный подход к вопросу о том, насколько большую выборку следует взять, несложен. В разделе Элементарные понятия статистики обсуждается понятие выборочного распределения. Если взять повторные выборки определенного объема из совокупности, скажем, поршневых колец, и вычислить их средние диаметры, то распределение этих средних значений будет приближаться к нормальному распределению с определенным средним значением и стандартным отклонением (или стандартной ошибкой; для выборочных распределений термин “стандартная ошибка” предпочтительнее, чтобы отличать изменчивость средних значений от изменчивости изделий в генеральной совокупности).


К счастью, нет необходимости брать повторные выборки из совокупности, чтобы оценить среднее значение и изменчивость (стандартную ошибку) выборочного распределения. Располагая хорошим представлением (оценкой) того, какова изменчивость (стандартное отклонение, или сигма) в данной совокупности, можно вывести выборочное распределение среднего значения. В принципе этой информации достаточно, чтобы оценить объем выборки, необходимый для обнаружения некоторого изменения качества (по сравнению с заданными спецификациями). Опуская детали соответствующих вычислительных процедур, рассмотрим вопрос о том, какие параметры должен иметь в своем распоряжении  инженер, чтобы провести соответствующие вычисления.

Средние для гипотез H0 и H1
Средние для гипотез H0 и H1

Чтобы формализовать процесс проверки, скажем, партии поршневых колец, нужно сформулировать две альтернативных гипотезы. Во-первых, можно предположить, что средние диаметры поршневых колец удовлетворяют техническим условиям. Эта гипотеза называется нулевой гипотезой (H0). Альтернативная гипотеза (H1), состоит в том, что диаметры поршневых колец отклоняются от технических условий больше, чем на определенную величину. Заметим, что можно сформулировать такого рода гипотезы не только для измерений, типа диаметров поршневых колец, но и для качественных характеристик (признаков). Например, можно предположить (H1), что доля дефектных изделий в партии превышает определенный процент (нулевая гипотеза). Естественно, что чем больше различие между H0 и H1, тем меньшего объема выборка необходима для обнаружения этого различия (см. раздел  Элементарные понятия статистики).

Вероятности ошибок альфа и бета
Вероятности ошибок альфа и бета

Возвращаясь к примеру с поршневыми кольцами, заметим, что существует два рода ошибок, которые можно сделать при проверке партии поршневых колец. Во-первых, можно ошибочно отвергнуть H0, то есть забраковать партию, решив, что диаметры поршневых колец отклоняются от заданных спецификаций.


Вероятность совершить такую ошибку обычно называется вероятностью ошибки первого рода (типа альфа). Вторая ошибка, которую можно сделать, –ошибочно не отвергнуть H0 (принять партию поршневых колец), когда на самом деле средний диаметр поршневых колец отклоняется от требуемого на определенную величину. Вероятность этой ошибки обычно называется вероятностью ошибки второго рода (типа бета). Ясно, что чем большая уверенность в правильном решении вам нужна, то есть чем ниже будут заданы вероятности ошибок первого и второго рода, тем большего объема выборки потребуются; фактически, чтобы быть уверенным на 100%, придется измерить каждое поставленное вашей компании поршневое кольцо.

Планы с фиксированным объемом выборки
Планы с фиксированным объемом выборки

Чтобы построить простой план выборочного контроля, сначала принимается решение об объеме выборки, основанное на средних значениях в предположении справедливости гипотез H0 или H1 и конкретных значениях вероятностей ошибок типа альфа и бета. Затем берется одна выборка этого фиксированного объема и на основании значения этого выборочного среднего принимается решение принять или отвергнуть данную партию. Такая процедура называется контролем с фиксированным объемом выборки (fixed sampling plan).

Кривая операционных характеристик (ОХ).
Кривая операционных характеристик (ОХ).

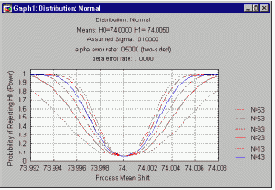
Мощность плана выборочного контроля с фиксированным объемом выборки можно представить с помощью кривой операционных характеристик. На графике вероятность отвергнуть H0 (и принять H1) откладывается по оси ординат как функция отклонения фактических значений, отложенных по оси абсцисс, от заданного (номинального) значения. Эта вероятность, разумеется, равна единице минус вероятность ошибки второго рода (ошибочно отвергнуть H1 и принять H0) и называется мощностью обнаружения отклонений для плана выборочного контроля с фиксированным объемом выборки. На графике показаны функции мощности для выборок разного объема.

Последовательные выборочные планы
Последовательные выборочные планы



В качестве альтернативы контролю с фиксированным объемом выборки можно случайным образом выбирать отдельные поршневые кольца и записывать их отклонения от номинала. Продолжая измерять каждое следующее выбранное поршневое кольцо, вычисляют текущую общую сумму отклонений от номинала (суммарное отклонение). Ясно, если гипотеза H1 верна, иными словами, если средний диаметр поршневых колец в данной партии отличается от номинального, то следует ожидать постепенного увеличения или уменьшения совокупного (накопленного) отклонения в зависимости от того, больше или меньше средний диаметр колец в партии, чем номинал. Такого рода последовательный выборочный контроль более чувствителен, чем контроль, основанный на выборке фиксированного объема. На практике отбор изделий продолжается до тех пор, пока партия не будет принята или забракована.

Применение последовательного выборочного контроля.
Применение последовательного выборочного контроля.

Вначале обычно строится график, на котором показывается накопленное отклонение от номинала (откладываемое на оси ординат) для последовательно отбираемых изделий (например, поршневых колец, номер которых в выборке откладывается по оси абсцисс). Затем на графике проводятся два набора прямых, обозначающих "коридор". Отбор изделий продолжается до тех пор, пока совокупное отклонение остается внутри данного коридора.



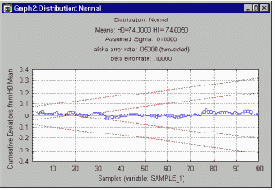
Отбор прекращается, если накопленное отклонение выходит из коридора. Если это значение поднимается выше верхней линии или опускается ниже нижней линии, партия забраковывается. Если накопленное отклонение выходит из коридора внутрь, то есть приближается к средней линии, партия принимается (это указывает на практически нулевое отклонение от номинала). Обратите внимание, что внутренняя область начинается с некоторого определенного номера, который соответствует минимальной величине объема выборки, необходимой для принятия решения о приемке партии изделий (при заданных вероятностях ошибки).

Выводы
Выводы

Итак, цель статистического контроля – использование статистического "заключения" для приемки или отбраковки всей партии изделий на основании изучения лишь сравнительно небольшого числа изделий из этой партии.


Преимущество применения статистических рассуждений при принятии такого решения состоит в возможности вычисления или задания в явном виде вероятностей принять ошибочное решение.

Всегда, когда возможно, последовательный выборочный контроль следует предпочесть контролю с фиксированным объемом выборки, так как он обладает большей мощностью. В большинстве случаев для принятия решения с той же степенью уверенности последовательный выборочный контроль в среднем требует анализа меньшего числа выборок, чем контроль с заранее фиксированным объемом выборки.

Оглавление

Анализ пригодности процесса Введение Методы вычислений Индексы (показатели) пригодности Пригодность и качество процесса Использование экспериментов для повышения пригодности Проверка предположения о нормальности распределения Доверительные границы Введение
Введение

См. также раздел Негауссовские распределения.

В разделе Контроль качества описано много методов оценки качества производственного процесса. Однако как только процесс становится управляемым, возникает следующий вопрос: "в какой степени долговременное поведение процесса удовлетворяет техническим условиям и целям, поставленным руководством?" Возвращаясь к примеру с поршневыми кольцами, можно спросить: какое количество использованных поршневых колец попадает в границы конструктивного допуска? В более общих терминах вопрос ставится так: "насколько данный процесс (или поставщик) способен производить изделия, удовлетворяющие техническим условиям?" Большинство описанных здесь процедур и характеристик производства сравнительно недавно внедрены в США компанией "Форд Моторс" (Kane, 1986). Они позволяют оценить пригодность процесса с помощью осмысленных показателей.

Сначала мы обсудим вычисление и интерпретацию показателей пригодности процесса для случая нормального распределения. Если распределение параметров качества не подчиняется нормальному закону, то возможны модифицированные показатели, вычисленные на основе квантилей подходящего аппроксимирующего распределения из числа негауссовских распределений (например, Вейбулла, логарифмически нормального, бета, гамма и др.) или из семейства распределений общего вида с помощью метода моментов.



Важное замечание.
Важное замечание.

Заметим, что нет смысла изучать пригодность производственного процесса, если он не управляем. Иными словами, если средние значения последовательных выборок сильно флуктуируют или явно находятся вне заданного допуска, то вначале нужно решить проблемы качества. Следовательно, первый шаг к организации высококачественного процесса производства состоит в том, чтобы сделать процесс управляемым с помощью методов, описанных в разделе Контроль качества.

Методы вычислений
Методы вычислений

Если процесс управляем, то можно ставить вопрос о его пригодности. Ответ на этот вопрос основывается на "статистических" рассуждениях и близок к обсуждавшейся ранее проблеме выборочного контроля. Возвращаясь к примеру с поршневыми кольцами, заметим, что если дана выборка определенного объема, то можно оценить стандартное отклонение процесса производства поршневых колец. Затем можно построить гистограмму распределения диаметров поршневых колец. Если распределение диаметров нормальное, то можно сделать выводы о доле поршневых колец, попадающих в границы допуска.



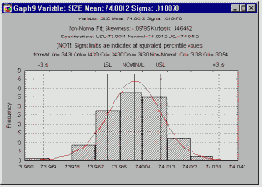
Для негауссовских распределений используется метод процентилей. Рассмотрим основные показатели пригодности, наиболее часто используемые для анализа производственных процессов.

Индексы (показатели) пригодности процесса
Индексы (показатели) пригодности процесса

Размах процесса.
Размах процесса.

Как правило, сначала находят границы ±3 сигма по обе стороны от номинала. На самом деле границы сигма должны быть те же самые, что применяются для обеспечения управляемости процесса с помощью контрольных карт (см. Контроль качества). Эти границы обозначают размах процесса. Если используется интервал ±3 сигма, то в предположении нормальности распределения можно сделать вывод о том, что примерно 99% всех поршневых колец находятся в этих границах.

Границы допуска НГД, ВГД.
Границы допуска НГД, ВГД.

Обычно технические условия задают некий диапазон допустимых значений. В данном примере считается приемлемым, если значения диаметров поршневых колец лежат в пределах 74.0 ± .02 мм.


Таким образом, нижняя граница допуска (lower specification limit – LSL) для данного процесса равна 74.0 - 0.02 = 73.98 , верхняя граница допуска (upper specification limit – USL) равна 74.0 + 0.02 = 74.02. Разность между НГД и ВГД называется размахом допуска (specification range).

Потенциальная пригодность (Cp).
Потенциальная пригодность (Cp).

Это простейший и самый естественный показатель пригодности производственного процесса. Он определяется как отношение размаха допуска к размаху процесса; при использовании границ ±3 сигма данный показатель можно выразить в виде

Cp = (ВГД-НГД)/(6*сигма)

Данное отношение выражает долю размаха кривой нормального распределения, попадающую в границы допуска (при условии, что среднее значение распределения является номинальным, то есть процесс центрирован, см. ниже).

В работе Bhote (1988) сообщается, что до повсеместного внедрения методов статистического контроля качества (до 1980 г.) обычное качество производственных процессов в США составляло примерно Cp = .67. Иными словами, два хвоста кривой нормального распределения, каждый из которых содержит примерно 15.5% общего количества изделий, попадали за границы допуска. В конце 80-х годов лишь около 30% производств в США находились на этом или еще худшем уровне качества (см. Bhote, 1988, стр. 51). В идеале, конечно, было бы хорошо, если бы этот показатель превышал 1, т.е. хотелось бы достигнуть такого уровня пригодности процесса, чтобы никакое (или почти никакое) изделие не выходило за границы допуска. Любопытно, что в начале 80-ых годов японская промышленность приняла в качестве стандарта Cp = 1.33! Пригодность процесса, требуемая для изготовления высокотехнологичных изделий, еще выше; компания Minolta установила показатель Cp = 2.0 как минимальный стандарт для себя (Bhote, 1988, стр. 53) и как общий стандарт для своих поставщиков. Заметим, что высокая пригодность процесса обычно приводит к более низкой, а не к более высокой себестоимости, если учесть затраты на рекламацию, связанную с низким качеством производимой продукции.


Этот пункт мы кратко обсудим ниже.

Отношение пригодности (Cr).
Отношение пригодности (Cr).

Этот индекс является обратным к показателю Cp и вычисляется как отношение 1/Cp.

Нижняя/верхняя потенциальная пригодность: Cpl, Cpu.
Нижняя/верхняя потенциальная пригодность: Cpl, Cpu.

Недостаток показателя Cp (и Cr) состоит в том, что он может дать неверную информацию о производственном процессе в том случае, если среднее процесса отличается от номинального, иными словами, если процесс не центрирован. Нецентрированность или смещенность процесса производства можно выразить следующим образом. Сначала можно вычислить верхний и нижний показатели пригодности, чтобы отразить отклонение наблюдаемого среднего процесса от НГД и ВГД. Приняв в качестве размаха процесса границы ±3 сигма, вычислим следующие показатели:

Cpl = (Среднее - НГД)/3*сигма
и
Cpu = (ВГД - Среднее)/3*сигма

Ясно, что если эти значения не совпадают, то процесс не центрирован.

Поправка на нецентрированность(K).
Поправка на нецентрированность(K).

Можно скорректировать индекс Cp, чтобы учесть смещение. А именно, вычислим:

k = abs(Номинал - Среднее)/(1/2(ВГД-НГД))

Этот поправочный множитель выражает отношение нецентрированности (номинал минус среднее) к допуску.

Подтвержденное качество (Cpk).
Подтвержденное качество (Cpk).

Наконец, Cp можно скорректировать, внеся поправку на нецентрированность посредством вычисления

Cpk = (1-k)*Cp

Если процесс идеально центрирован, то k равно нулю и Cpk равно Cp. Однако когда процесс смещается от номинального значения, k увеличивается, и Cpk становится меньше Cp.

Потенциальная пригодность II: Cpm.
Потенциальная пригодность II: Cpm.

Недавно введенная модификация показателя Cp (Chan, Cheng, and Spiring, 1988) направлена на уточнение оценки сигмы с целью учесть влияние случайной нецентрированности. При этом вычисляется другое значение, а именно, Сигма2:

Сигма2 = { (xi - Номинал)2/(n-1)}

где
Сигма2- другая оценка сигма,
xi                - значение i-го выборочного наблюдения,


Номинал   - значение номинала,
n                 - число наблюдений в выборке.

Затем можно использовать эту оценку параметра сигма при вычислении Cp по тем же формулам, что и прежде. Полученный показатель будет обозначаться Cpm.

Качество и пригодность процесса
Качество и пригодность процесса

При контроле процесса с помощью карт контроля качества (например, X- или R карты; см. раздел Контроль качества) часто бывает полезно вычислять показатели пригодности процесса. Когда набор данных состоит из нескольких выборок, то можно вычислить два разных показателя изменчивости. Один из них – обычное стандартное отклонение для всех наблюдений, не принимающее в расчет, что данные состоят из нескольких выборок; другой показатель оценивает собственный разброс процесса по изменчивости внутри выборки. Например, при построении X- или R карт можно использовать обычную оценку R_/d2 для сигмы процесса (см., например, Duncan, 1974; Montgomery, 1985). Заметим, однако, что эта оценка применима только тогда, когда процесс статистически устойчив. Подробное обсуждение различия между общей и собственной изменчивостью процесса содержится в справочном руководстве ASQC/AIAG (ASQC/AIAG, 1991, стр. 80).

Когда при стандартных вычислениях пригодности используется общая изменчивость процесса, полученные показатели обычно называют показателями качества процесса (process performance) (поскольку они описывают фактическое поведение процесса), тогда как показатели, вычисленные исходя из собственного разброса (сигма выборки), называются показателями пригодности (поскольку они описывают собственную пригодность процесса).

Использование экспериментов для повышения пригодности
Использование экспериментов для повышения пригодности

Как уже отмечалось, чем выше показатель Cp, тем лучше процесс – и это соотношение не знает верхнего предела. Вопросы цены качества, т.е. убытков, связанных с плохим качеством, подробно обсуждаются в связи с методами робастных экспериментов Тагучи (см.


раздел  Планирование эксперимента). Как правило, более высокое качество обычно приводит к снижению общей себестоимости. Хотя издержки производства при этом увеличиваются, но убытки, вызванные плохим качеством, например, из-за рекламаций потребителей, потери доли рынка и т.п., обычно намного превышают затраты на контроль качества. На практике два или три хорошо спланированных эксперимента, проведенных в течение нескольких недель, часто позволяют достичь значения показателя Cp, равного 5 или выше. Если вы не знакомы с планированием экспериментов, но интересуетесь качеством процесса, настоятельно рекомендуем ознакомиться с обзором методов, подробно описанных в главе Планирование эксперимента.

Проверка предположения о нормальности распределения
Проверка предположения о нормальности распределения

Только что рассмотренные показатели имеют смысл только тогда, когда измеряемые параметры качества действительно подчиняются нормальному распределению (показатели пригодности для распределений, отличных от нормального, будут введены ниже). Существуют специальные критерии для проверки предположения о нормальности (например, критерий Колмогорова-Смирнова или критерий хи-квадрат), которые описаны в большинстве учебников по статистике и подробно обсуждаются в разделе Непараметрическая статистика и подгонка распределений .

Визуальная проверка на нормальность проводится с помощью графиков вероятность-вероятность (В-В) и квантиль-квантиль (К-К) для нормального распределения. Ниже, после обсуждения показателей пригодности для распределений, отличных от нормального, эти графики будут рассмотрены более подробно.

Доверительные границы
Доверительные границы

До введения в начале 80-тых годов показателей пригодности общим методом описания характеристик производственного процесса был расчет и изучение границ доверительного интервала этого процесса (см., например, Hald, 1952). Смысл этой процедуры таков. Сначала предположим, что соответствующий параметр качества нормально распределен на совокупности выпускаемых изделий; тогда можно подсчитать верхнюю и нижнюю границы интервала, гарантирующие с определенным доверительным уровнем (вероятностью), что определенный процент совокупности находится в этих пределах.


Другими словами, если заданы: конкретный объем выборки (n), среднее процесса, стандартное отклонение (сигма), доверительный уровень и процент совокупности, который должен попасть в интервал, то можно вычислить соответствующие границы доверительного интервала, удовлетворяющие всем заданным параметрам. Кроме того, существует возможность расчета непараметрических границ доверительного интервала, не основанных на предположении нормальности распределения (Scheffe и Tukey, 1944, стр 217; Wilks, 1946, стр 93; см. также Duncan, 1974, или Montgomery, 1985, 1991).

См. также раздел Негауссовские распределения.

Оглавление

Повторяемость и воспроизводимость измерений Введение Методы вычислений Графики повторяемости и воспроизводимости Компоненты дисперсии Выводы Введение
Введение

Анализ повторяемости и воспроизводимости связан с изучением вопроса о точности измерений. Цель анализа повторяемости и воспроизводимости – определить, какая часть изменчивости результатов измерений вызвана (1) различием измеряемых изделий или деталей (изменчивость деталей), (2) различием операторов или приборов, осуществляющих измерения, (воспроизводимость) и (3) ошибками (погрешностями) измерений, осуществляемых теми же операторами при нескольких измерениях одинаковыми приборами одних и тех же деталей (повторяемость). В идеальном случае все колебания результатов измерений вызваны изменчивостью самих деталей, и лишь пренебрежимо малая часть зависит от воспроизводимости (приборов и операторов) и повторяемости (повторных измерений).

Если вернуться к примеру с поршневыми кольцами, то для обнаружения отклонения диаметров от номинального на 0.01 мм потребуются измерительные приборы (калибры) соответствующей точности. Описываемые далее процедуры позволяют инженеру вычислить необходимую точность инструментов и разных операторов, использующих их, в сравнении с разбросом параметров деталей внутри выборки.

Стандартные показатели повторяемости, воспроизводимости и изменчивости деталей можно вычислить на основе размахов (как это все еще принято в таких экспериментах) или с помощью анализа таблицы дисперсий (ДА) (как, например, рекомендуется в ASQC/AIAG, 1990, стр. 65).


Кроме того, таблица дисперсионного анализа содержит F-тест (проверку статистической значимости) взаимодействия оператор-деталь и выдает оценки дисперсий, стандартных отклонений и доверительных интервалов для компонент модели дисперсионного анализа.

Наконец, можно рассчитать соответствующие проценты полной изменчивости и получить так называемую статистику допустимости. Дополнительную информацию можно найти в Duncan (1974), Montgomery (1991) и в DataMyte Handbook (1992); иллюстрированные инструкции с примерами представлены в публикациях ASQC/AIAG Measurement systems analysis reference manual (1990) и Fundamental statistical process control reference manual (1991).

Обратите внимание, что существуют и другие процедуры для анализа различных типов планов, которые подробно описаны, например, в разделе Методы дисперсионного анализа. Методы, описанные в разделе Компоненты дисперсии и смешанные модели дисперсионного анализа, целесообразно использовать для анализа очень больших вложенных планов (которые имеют более 200 уровней) или иерархических вложенных планов (со случайными эффектами или без них).

Методы вычислений
Методы вычислений

Каждое измерение можно считать состоящим из компонент, связанных: с характеристиками измеряемой детали или изделия, с надежностью измерительного прибора, с особенностями оператора (человека, применяющего измерительный прибор). По определению, метод измерения (измерительная система) воспроизводим, если разные использующие его операторы получают идентичные или очень близкие результаты. Метод измерения повторяем, если повторные измерения одной той же детали дают идентичные результаты. Обе эти характеристики – повторяемость и воспроизводимость – влияют на точность измерительной системы. Можно спланировать эксперимент для оценивания величин каждой компоненты, т.е. повторяемости, воспроизводимости и изменчивости деталей, и таким образом оценить точность измерительной системы. По существу эта процедура сводится к дисперсионному анализу (ДА) плана многофакторного эксперимента, включающего в качестве факторов разные детали, операторов и повторные измерения (испытания).


Тогда можно вычислить соответствующие компоненты дисперсии, чтобы оценить повторяемость (дисперсию, связанную с различиями результатов повторных испытаний), воспроизводимость (дисперсию, связанную с различиями между операторами), и изменчивость деталей (дисперсию, связанную с различиями между деталями). Если вы не знакомы с основной идеей дисперсионного анализа, рекомендуем вам прочитать соответствующий раздел. Описанные там методы можно использовать в том числе и для процедур анализа повторяемости и воспроизводимости.

Графики повторяемости и воспроизводимости
Графики повторяемости и воспроизводимости

Существует несколько способов графически представить результаты экспериментального исследования повторяемости и воспроизводимости. Предположим, что вы производите небольшие сушильные шкафы (печи), применяемые для сушки материалов, используемых в других производственных процессах. Эти печи должны работать при номинальной температуре около 100 градусов Цельсия. В данном исследовании 5 разных инженеров (операторов) трижды (три опыта) измерили одну и ту же выборку из 8 печей (деталей). Можно построить график средних значений измерения каждой из 8 деталей каждым оператором. Если измерительная система воспроизводима, то характер изменения средних по трем опытам от детали к детали должен быть сходным для всех 5 инженеров, принявших участие в исследовании.

R и S карты.
R и S карты.

В разделе Контроль качества подробно обсуждается концепция R(размах) и S(сигма) карт для контроля за изменчивостью процесса. Можно применить эти концепции в данной ситуации и построить график размахов (или сигм) для операторов и деталей; эти графики позволят выявить сильные отклонения (выбросы) среди операторов и деталей. Если какой-нибудь оператор дает особенно большой разброс измерений, вам захочется выяснить, почему именно у него возникли трудности с получением надежных результатов (например, возможно, он неправильно понял инструкции по использованию измерительного прибора).



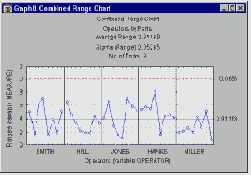
Аналогичным образом, R карта для деталей позволяет выявить детали, для которых особенно трудно получить надежные измерения; исследование этой конкретной детали может помочь понять недостатки применяемой измерительной системы.





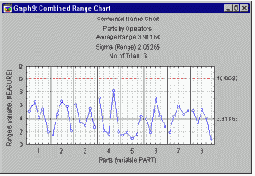
Итоговый график повторяемости и воспроизводимости.
Итоговый график повторяемости и воспроизводимости.

На итоговом графике показаны индивидуальные измерения, сделанные каждым инженером (оператором). Измерения представлены отклонениями от соответствующих средних значений для соответствующей детали. Каждое измерение показано на графике в виде точки, а результаты опытов, проведенных для каждой детали конкретным оператором, соединены вертикальными линиями. Точки, представляющие сделанные каждым инженером измерения, заключены в прямоугольник ("ящик"), показывающий общий разброс измерений, сделанных соответствующим оператором (см. следующий рисунок).



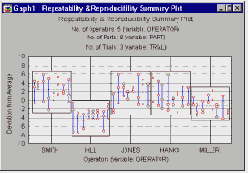
Компоненты дисперсии (см. также раздел Компоненты дисперсии)
Компоненты дисперсии (см. также раздел Компоненты дисперсии)

Доля изменчивости и процент допуска.
Доля изменчивости и процент допуска.

Величина процента допуска позволяет оценить качество измерительной системы по отношению к общей изменчивости процесса и соответствующему размаху допуска. При этом можно задать диапазон допуска и число сигма-интервалов. Параметр Число сигма-интервалов будет использован для расчета соответствующей величины изменчивости, обусловленной повторяемостью, воспроизводимостью, изменчивостью деталей и т.п. Как правило, число сигма-интервалов берется равным 5.15. В этот диапазон попадает 99% площади под кривой номального распределения. Это означает, что такой интервал будет включать 99% всех значений с соответствующими характеристиками изменчивости.

Процент от общей изменчивости.
Процент от общей изменчивости.

Эта величина характеризует долю изменчивости, обусловленную различными источниками (компонентами), по отношению к общей изменчивости (размаху) измерений.

Анализ дисперсии.
Анализ дисперсии.

Помимо вычислений оценок компонент дисперсии по размахам, существует более точный метод, основанный на дисперсионном анализе (см. Duncan, 1974, ASQC/AIAG, 1990 ).

Можно рассматривать три фактора R & R эксперимента (Операторы, Детали, Опыты) как случайные факторы в трехфакторной модели дисперсионного анализа.


Подробную информацию о традиционно рассматриваемых моделях можно найти в публикации ASQC/AIAG (1990, стр. 92-95) или в работе Duncan (1974, стр. 716-734). Обычно взаимодействия фактора испытаний (опытов) со всеми другими факторами считают несущественными. Это разумно, поскольку трудно представить, как могут возникать систематические ошибки измерения некоторых деталей при повторных опытах, особенно если порядок деталей и опытов случаен.

В отличие от этого взаимодействие Операторы-Детали может быть существенным. Так, естественно ожидать, что некоторые менее опытные операторы будут склонны к каким-то специфическим ошибкам, что приведет к систематическим искажениям при измерении определенных деталей. Поэтому можно ожидать, что эти факторы взаимодействуют (см. описание терминов дисперсионного анализа в соответствующем разделе).

В том случае, когда парные взаимодействия статистически значимы, можно отдельно оценить компоненты дисперсии, порожденные различиями операторов и связанные с взаимодействием операторов и деталей. При наличии значимого взаимодействия суммарная изменчивость, связанная с повторяемостью и воспроизводимостью, определяется как сумма трех компонент: повторяемости (ошибок измерения), ошибок оператора и ошибок оператора по данной детали.

Если взаимодействие операторов и деталей не является статистически значимым, можно пользоваться более простой аддитивной моделью без взаимодействий.

Выводы
Выводы

Итак, цель изучения повторяемости и воспроизводимости – позволить инженеру, отвечающему за контроль качества, оценить точность используемой в процессе измерительной системы. Очевидно, что измерительная система с плохой повторяемостью (большим разбросом между опытами) или воспроизводимостью (большим разбросом для разных операторов) по сравнению с разбросом при измерении разных деталей не пригодна для контроля качества. Например, полученные с ее помощью результаты нельзя использовать при построении карт контроля качества и в процедурах оценки пригодности и выборочного контроля при анализе производственных процессов.

Оглавление

Негауссовские распределения Введение Подгонка распределений методом моментов Качество подгонки: графики квантилей и вероятностей Негауссовские индексы пригодности (метод процентилей) Введение
Введение

Основное назначение.
Основное назначение.

Концепция анализа пригодности подробно рассматривается в разделе Анализ пригодности. Анализируя качество процесса (например, производственного), полезно оценить долю изделий, выходящих за границы заранее заданного диапазона допустимых значений (допуска). Например, так называемый показатель Cp вычисляется по формуле:

Cp = (ВГД - НГД)/(6*сигма)

где сигма – это оценка стандартного отклонения процесса, а ВГД и НГД – это верхняя и нижняя границы допуска соответственно. Если распределение соответствующего параметра качества или переменной (например, диаметров поршневых колец) нормальное и процесс идеально центрирован (т.e. среднее процесса равно номиналу), то этот показатель можно интерпретировать как долю стандартной кривой нормального распределения (ширины процесса), попадающую в предписанные техническими условиями границы. Если процесс не центрирован, используется скорректированный показатель Cpk.

Негауссовские распределения.
Негауссовские распределения.

Наблюдаемую гистограмму можно аппроксимировать отличным от нормального распределением и вычислить показатели пригодности с помощью так называемого метода процентилей. Помимо конкретных распределений можно использовать для расчета показателей пригодности два общих семейства распределений – Джонсона (Johnson, 1965; см. также Hahn and Shapiro, 1967) и Пирсона (Johnson, Nixon, Amos, and Pearson, 1963; Gruska, Mirkhani, and Lamberson, 1989; Pearson and Hartley, 1972), которые позволяют аппроксимировать широкий спектр непрерывных распределений. Для всех распределений можно также вычислить таблицы ожидаемых частот, ожидаемое число наблюдений, выходящих за рамки технических условий, и построить графики квантиль-квантиль (К-К) и вероятность-вероятность (В-В) (см.


ниже). Конкретный метод вычисления показателей пригодности процесса на основе этих распределений описан в работе Clements (1989).

Графики квантиль-квантиль и вероятность-вероятность.
Графики квантиль-квантиль и вероятность-вероятность.

Существуют различные методы оценки качества подгонки к наблюдаемым данным. Кроме таблицы наблюдаемых и ожидаемых частот для разных интервалов и критериев качества подгонки Колмогорова-Смирнова и хи-квадрат, можно построить графики квантилей и вероятностей для всех распределений. Эти диаграммы рассеяния строятся таким образом, что если распределение наблюдаемых значений соответствует теоретическому, то точки наблюдений ложатся на графике на прямую линию.

Подгонка распределений методом моментов
Подгонка распределений методом моментов

Кроме некоторых конкретных типов распределений можно использовать для аппроксимации распределения из общих "семейств" – так называемые кривые Джонсона и Пирсона, имеющие те же первые четыре момента, что и наблюдаемое распределение.

Общий подход.
Общий подход.

Форму большинства непрерывных распределений в ряде случаев можно достаточно полно охарактеризовать первыми четырьмя моментами. Если аппроксимировать гистограмму наблюдений распределением, имеющим то же среднее (первый момент), дисперсию (второй момент), асимметрию (третий момент) и эксцесс (четвертый момент), то общая форма полученной кривой может достаточно хорошо соответствовать наблюдаемому распределению. Далее по этой кривой можно вычислить процентили и оценить долю изделий, которые удовлетворяют техническим условиям.

Кривые Джонсона.
Кривые Джонсона.

В 1949 году Джонсон описал систему плотностей вероятности, представляющих собой преобразования стандартной кривой нормального распределения (см. подробности в Hahn and Shapiro, 1967). Применением этих преобразований к стандартной нормальной величине можно аппроксимировать различные, отличные от нормального распределения, включая распределения, сосредоточенные на интервалах и полуинтервалах (например, U-образные).


Преимущество этого подхода в том, что после подгонки конкретной кривой Джонсона для вычисления ожидаемых значений процентных точек этой кривой можно использовать нормальную функцию распределения. Методы подгонки кривых Джонсона по первым четырем моментам эмпирического распределения подробно описаны в Hahn and Shapiro, 1967, стр. 199-220; и в Hill, Hill, and Holder, 1976.

Кривые Пирсона.
Кривые Пирсона.

Другая система плотностей предложена Карлом Пирсоном (см. например, Hahn and Shapiro, 1967, стр. 220-224). Эта система состоит из семи решений дифференциального уравнения (из 12, первоначально перечисленных Пирсоном), которые тоже аппроксимируют широкое разнообразие кривых разной формы. Gruska, Mirkhani, and Lamberson (1989) подробно описали, как подогнать к данным различные кривые Пирсона. Метод вычисления конкретных процентилей кривых Пирсона также описан в работе Davis and Stephens (1983).

Качество подгонки: графики вероятностей и квантилей
Качество подгонки: графики вероятностей и квантилей

Для каждого распределения можно вычислить таблицу ожидаемых и наблюдаемых частот и значения критерия хи-квадрат, а также d-критерия Колмогорова-Смирнова. Тем не менее, сначала лучше использовать визуальные методы оценки качества подгонки. Для этого применяются два стандартных графика: квантиль-квантиль и вероятность-вероятность.

Графики квантиль-квантиль.
Графики квантиль-квантиль.

На графиках квантиль-квантиль (кратко, К-К) наблюдаемые значения переменной откладываются напротив теоретических квантилей. Чтобы построить К-К график, n наблюдаемых значений упорядочиваются в порядке возрастания (строится вариационный ряд наблюдений):

x1 x2 ... xn

По одной оси графика откладываются полученные порядковые статистики, а по другой значения:

F-1 ((i-radj)/(n+nadj))

где i – ранг соответствующего наблюдения, radj и nadj – поправки ( 0.5), а F-1 означает обратную функцию распределения для соответствующего нормированного распределения. Полученный график представляет собой диаграмму рассеяния наблюдаемых значений относительно (нормированных) ожидаемых значений при заданном распределении.


Заметим, что кроме величины обратной функции распределения, на противоположной оси графика можно отложить функцию распределения, т.е. не только нормированные значения теоретического распределения, но и соответствующие значения вероятности.



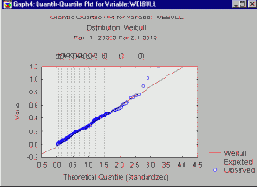
Хорошее соответствие теоретического распределения наблюдаемым значениям проявится на этом графике, если нанесенные на него точки расположатся вдоль прямой линии. Заметим, что поправки radj и nadj обеспечивают попадание аргумента для обратной функции распределения, в интервал между 0 и 1, но не включая 0 и 1 (см. Chambers, Cleveland, Kleiner, and Tukey, 1983).

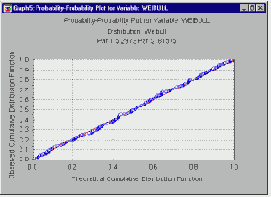
Графики вероятность-вероятность.
Графики вероятность-вероятность.

На графиках вероятность-вероятность (кратко В-В) наблюдаемая функция распределения откладывается на одной оси, а теоретическая функция распределения – на другой. Как и для графиков К-К, значения соответствующей переменной сначала упорядочиваются в порядке возрастания. Наблюдение с номером i откладывается по одной оси как i/n (т.е. наблюдаемая функция распределения), а по другой оси как F(x(i)), где F(x(i)) обозначает величину теоретической функции распределения для соответствующего наблюдения x(i). Если теоретическая функция распределения хорошо аппроксимирует наблюдаемое распределение, то все точки на этом графике должны попасть на диагональную линию (как на показанном ниже рисунке).



Негауссовские индексы пригодности (метод процентилей)
Негауссовские индексы пригодности (метод процентилей)

Как уже отмечалось ранее, показатели пригодности в общем случае вычисляются для того, чтобы оценить качество процесса, т.е. чтобы получить оценки разброса производимых изделий (размах процесса) по отношению к размаху допуска. Для стандартных показателей пригодности процесса, основанных на нормальном распределении, размах процесса обычно определяется как 6 сигма, т.е. как плюс-минус утроенная оценка стандартного отклонения процесса. Для стандартной кривой нормального распределения эти границы (zl = -3 и zu = +3) пересчитываются в 0.135 и 99.865 процентили соответственно.


Для распределений, отличных от нормального, границы 3 сигма, а также среднее (zM = 0.0) можно заменить соответствующими стандартными значениями, дающими те же величины процентилей под кривой негауссовского распределения. Эта процедура подробно описана в работе Clements (1989).

Индексы (показатели) пригодности.
Индексы (показатели) пригодности.

Ниже приведены формулы для вычисления негауссовских показателей пригодности:

Cp = (ВГД-НГД)/(Up-Lp)

CpL = (M-НГД)/(M-Lp)

CpU = (ВГД-M)/(Up-M)

Cpk = Min(CpU, CpL)

В этих уравнениях M обозначает медиану (50 процентиль) соответствующего распределения, а Up и Lp – 99.865 и 0.135 процентили соответственно, в случае если вычисления основываются на размахе процесса, равном ±3 сигма. Обратите внимание, что значения Up и Lp могут быть другими, если размах процесса задан другими границами (например, ±2 сигма).

Оглавление

Анализ Вейбулла, надежность и времена отказов
Анализ Вейбулла, надежность и времена отказов

Основные задачи Распределение Вейбулла Цензурированные наблюдения Двух- и трехпараметрическое распределение Вейбулла Оценка параметров Критерии согласия Интерпретация результатов Группированные данные Изменения порядка времен отказов для многократно цензурированных данных Функция распределения Вейбулла, надежность и функции риска Одной из основных характеристик качества продукции является ее надежность. Для оценки надежности и времени жизни применяются различные статистические методы, описание которых можно найти в книгах Lawless (1982), Nelson (1990), Lee (1980, 1992), and Dodson (1994); функция интенсивности (риска) для распределения Вейбулла описывается также в разделе Распределение Вейбулла, функция надежности, функция риска. Заметим, что похожие статистические процедуры используются также в анализе выживаемости (см. раздел Анализ выживаемости), а в книге Lee (1992) дается введение в эти методы для медико-биологических исследований; замечательный обзор со множеством инженерных примеров можно найти в работе Dodson (1994).



Основные задачи
Основные задачи

Надежность устройства или образца продукции является важным показателем качества. Особенный интерес представляет количественная оценка надежности, позволяющая оценить ожидаемое время жизни или, в инженерных терминах, время безотказной работы прибора. Предположим, вы летите на маленьком самолете с одним двигателем. Тогда для вас жизненно важно знать вероятность отказа двигателя на различных этапах его эксплуатации (например, после 500 часов работы , после 1000 часов и т.д.) Имея хорошую оценку надежности двигателя и доверительный интервал, можно принять рациональное решение о том, когда следует заменить двигатель или отправить его на капитальный ремонт.

Распределение Вейбулла
Распределение Вейбулла

Для описания времен отказов образцов, поставленных на испытание, традиционно используется распределение Вейбулла (см. также раздел Распределение Вейбулла, функция надежности и функция риска), названное в честь шведского исследователя Валоди Вейбулла (Waloddi Weibull), применявшего его для описания времен отказов разного типа; в России исследование этого распределения связано с именем известного русского математика Б.В. Гнеденко, бывшего долгие годы профессором Московского Университета, и часто называется распределением Вейбулла-Гнеденко (см. также Hahn and Shapiro, 1967; распределение Вейбулла-Гнеденко использовалось для описания времен жизни электронных устройств, ламп, подшипников и даже некоторых финансовых задач). Функция интенсивности и U-образная кривая.
Функция интенсивности и U-образная кривая.

Часто при проведении анализа надежности естественно рассматривать вероятность отказа в течение малого интервала времени при условии, что в начале интервала отказа не произошло. Такая функция называется функцией риска или функцией интенсивности отказов и формально определяется следующим образом:

h(t) = f(t)/(1-F(t))

где h(t) обозначает функцию интенсивности отказов или функцию риска в момент t, f(t)- плотность, а F(t) - функцию распределения времен отказов.


Для большинства исследуемых изделий (компонент, устройств и т.д.) функция интенсивности имеет форму U- образной кривой: на ранней стадии жизни изделия риск его выхода из строя (отказ) достаточно велик (так называемая детская смертность), далее интенсивность отказов уменьшается до определенного предела, а затем вновь увеличивается из-за старения (износа) изделия до тех пор, пока все детали не выйдут из строя.

Например, автомобили в начале эксплуатации часто имеют несколько мелких дефектов, приводящих к поломке. После того как автомобиль прошел обкатку, риск его выхода из строя существенно уменьшается. Затем интенсивность отказов (поломок) возрастает, достигая в конце концов своего максимального значения (обычно после 20 лет эксплуатации или 250000 миль пробега практически всякий автомобиль выходит из строя). Типичная U-образная функция интенсивности или функция риска выглядит следующим образом:



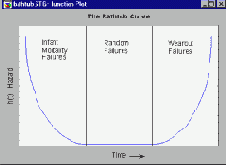
Распределение Вейбулла позволяет гибко моделировать различные возникающие на практике формы функции интенсивности. Задавая разные параметры распределения, можно получить практически любые функции риска. Ниже показаны функции интенсивности для параметров c=.5, c=1, c=2 и c=5.



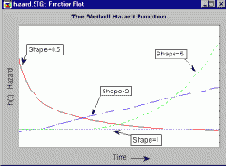
Ясно, что начальная фаза кривой аппроксимируется распределением Вейбулла с параметром формы c<1, постоянная фаза имеет параметр формы c=1, а финальная фаза (старение или износ) моделируется распределением с параметром формы c>1.

Функция распределения и функция надежности.
Функция распределения и функция надежности.

После того как оценены параметры распределения Вейбулла, можно оценить различные характеристики надежности. В частности, вычислить функцию распределения отказов (обычно обозначаемую как F(t)). Затем вы можете определить процентили функции выживаемости или функции надежности, например, оценить момент времени, когда откажет заданная доля тестируемых объектов.

Функция надежности (обычно обозначаемая как R(t)) определяется равенством R(t)=1-F(t)); иногда она называется также функцией выживания (т.к.


описывает вероятность того, что отказ произойдет после определенного момента времени t; см. например, Lee, 1992). Ниже показаны функции надежности для распределения Вейбулла, имеющие различные параметры формы.



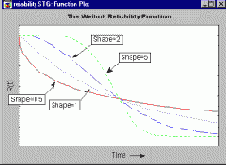
Если параметры формы меньше 1, то функция надежности резко уменьшается в начале времени жизни, затем уменьшение происходит более медленно. Если параметр формы больше 1, то сначала наблюдается небольшое уменьшение надежности, а затем, начиная с некоторой точки, она довольно быстро снижается. Точка, где все кривые пересекаются, называется характеристическим временем жизни и определяет момент, когда отказало 63.2% выборки (R(t) = 1-0.632 = .368). Эта точка равна соответствующему параметру масштаба b двухпараметрического распределения Вейбулла с параметром =0 (иначе это время соответствует b+).

Формулы для вычисления соответствующих характеристик приведены в разделе Распределение Вейбулла, надежность и функции риска.

Цензурированные наблюдения
Цензурированные наблюдения

При проведении большинства исследований надежности не все наблюдения завершаются отказами. Как правило, на завершающем этапе исследования становится ясно, что определенное количество объектов не отказало и точные времена их жизни неизвестны. Такие наблюдения называются цензурированными наблюдениями. Идея цензурирования и методы анализа цензурированных данных подробно описаны в разделе Анализ выживаемости. Заметим, что цензурирование может осуществляться очень разными способами, т.к. имеется много различных методов проверки надежности.

Цензурирование типа I и типа II.
Цензурирование типа I и типа II.

Так называемое цензурирование типа I применяется в ситуации, когда заранее фиксируется время проведения наблюдений (мы берем 100 ламп и оканчиваем эксперимент спустя некоторое промежуток времени, например, через 120 часов после начала). В этом случае интервал времени зафиксирован и число отказавших (перегоревших) ламп представляет собой случайную величину. При цензурировании типа II заранее задается доля (процент) отказов, но время наблюдения не фиксируется (например, мы проводим эксперимент пока не перегорят 50% ламп).


Очевидно при данном подходе мы имеем фиксированное число отказов, а время, в течение которого проводится эксперимент, является случайной величиной.

Левое и правое цензурирование.
Левое и правое цензурирование.

Дополнительно можно регулировать такой параметр, как направление цензурирования. В предыдущем примере цензурирование происходит всегда в правом направлении по временной оси (правое цензурирование), потому что исследователь точно фиксирует начало эксперимента и знает, что не отказавшие лампы будут действовать еще некоторое время после окончания эксперимента. Другой вариант возникает, когда исследователю не известно начало времени жизни объекта, например, врачу известен момент поступления пациента в госпиталь с данным диагнозом, но врач не знает, когда данный диагноз был поставлен и тем более не знает, когда болезнь началась. Такое цензурирование называется левым. Конечно, если тестируются старые лампы, то это тоже пример левого цензурирования, т.к. не известен момент начала их эксплуатации.

Однократное и многократное цензурирование.
Однократное и многократное цензурирование.

Наконец, возможны ситуации в которых цензурирование происходит в различные моменты времени (многократное цензурирование), или только в один момент времени (однократное цензурирование). Возвращаясь к эксперименту с электрическими лампами, заметим, что если эксперимент заканчивается в определенный момент времени, то мы имеем однократное цензурирование. Однако в медико-биологических исследованиях часто имеют дело с многократным цензурированием, например, продолжительность лечения и момент выписки могут быть разными для разных пациентов, и в то же время после выписки исследователь точно знает, что пациенты пережили все этапы лечебной процедуры.

Рассматриваемые методы применимы прежде всего к правому цензурированию, а также к однократно или многократно цензурированным данным.

Двух- и трехпараметрическое распределение Вейбулла
Двух- и трехпараметрическое распределение Вейбулла

Распределение Вейбулла ограничено с левой стороны.


Если вы посмотрите на график плотности распределения, то увидите, что значение x- должно быть больше 0. В большинстве случаев параметр положения (theta) известен (обычно равен 0) и определяет минимальное время жизни. Однако иногда оказывается, что вероятность отказа образца равна 0 спустя некоторое время после начала эксперимента, в таких ситуациях естественно считать, что параметр положения больше 0 (распределение сдвинуто вправо на некоторую величину), и необходимо осуществлять подгонку трехпараметрического распределения Вейбулла, используя различные методы оценки параметра положения. На практике Додсон (Dodson, 1994) рекомендует после подгонки двухпараметрического распределения Вейбулла обратить внимание на хвосты вероятностного графика, а также большие (>6) значения параметра формы, поскольку эти характеристики могут свидетельствовать о ненулевом значении параметра положения и необходимости подгонки трехпараметрической модели.

Оценка параметров

Оценки максимального правдоподобия.
Оценки максимального правдоподобия.

Для получения оценок максимального правдоподобия параметров двух- или трехпараметрического распределения Вейбулла используются стандартные итерационные методы минимизации функций. Особенности этих методов оценивания изложены в книге Dodson (1994); подробное описание итерационного метода Ньютона-Рафсона для численного построения оценок максимального правдоподобия можно найти в книге Keats and Lawrence (1997).

Оценка параметра положения для трехпараметрического распределения Вейбулла связана с рядом вычислительных трудностей (см., например, Lawless, 1982). В частности, если параметр формы меньше 1, то не существует оценок максимального правдоподобия параметров. В других случаях функция правдоподобия может иметь несколько локальных максимумов. В последнем случае Лоулесс (Lawless) рекомендует использовать для оценки параметра положения наименьшее время отказа (или значение чуть меньшее его).

Вероятностные графики, основанные на рангах.
Вероятностные графики, основанные на рангах.



Независимо от типа распределения можно оценить функцию распределения, используя:

Медианный (серединный) ранг:

F(t) = (j-0.3)/(n+0.4)

Cредний ранг:

F(t) = j/(n+1)

Параметр Уайта:

F(t) = (j-3/8)/(n+1/4)

где j обозначает порядок отказов или ранг до момента t (для многократного цензурирования вычисляются взвешенные порядковые моменты отказа, см. Dodson, p. 21), n – общее число наблюдений. Таким образом, можно построить следующий график.



Заметим, что горизонтальная ось графика имеет логарифмический масштаб; по вертикальной оси отложен log(log(100/(100-F(t))) (вероятностная шкала показана на левой оси y). График позволяет оценить два параметра распределения Вейбулла; в частности, параметр формы равен угловому коэффициенту (slope) прямой линии, а параметр масштаба оценивается как exp(-intercept/slope).

Оценка параметра положения по вероятностным графикам.
Оценка параметра положения по вероятностным графикам.

Представленный выше график показывает, что регрессионная прямая обеспечивает хорошую подгонку к данным. Если параметр положения определен неверно (например, не равен 0), то линейная подгонка оказывается значительно хуже. Поэтому имеет смысл построить вероятностные графики для нескольких значений параметра положения, как показано на следующей иллюстрации.



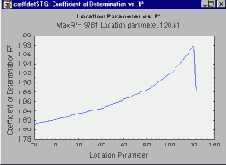
На приведенном выше рисунке, построенном на основе данных из работы Dodson (1994, Table 2.9), показан коэффициент детерминации R-квадрат (квадрат множественного коэффициента корреляции), который обычно используется для оценки качества линейной подгонки на вероятностном графике. При этом на оси x отложены различные значения параметра положения. Такой график часто бывает полезен, когда процедуры построения оценок максимального правдоподобия для трехпараметрического распределения Вейбулла не дают желаемого результата. С его помощью можно понять, существует ли единственное оптимальное значение параметра положения (как на показанном выше графике) или мы имеем дело с несколькими локальными максимумами.

График функции риска или интенсивности отказов.


График функции риска или интенсивности отказов.

Другой метод оценивания параметров двухпараметрического распределения Вейбулла – графический анализ функции интенсивности (как обсуждалось выше, функция интенсивности или, как ее часто называют, функция риска равняется вероятности наступления отказа в малый интервал времени [t, t + dt) при условии что до момента t отказ не произошел). Этот графический метод аналогичен методу оценки параметров из вероятностного графика функции надежности. Вначале строится график кумулятивной функции интенсивности (по оси х откладываются логарифмы времен жизни); тогда подогнанная регрессионная прямая дает наглядное представление о параметрах распределения. Как и в вероятностных графиках параметр формы оценивается через угол наклона регрессионной прямой, а параметр масштаба может быть оценен как exp(-св.член/коэф.наклона). Подробности можно найти в работе Dodson (1994), а некоторые формулы - в разделе Распределение Вейбулла, надежность и функция риска.

Метод моментов.
Метод моментов.

Идея этого метода, широко обсуждаемого в литературе, состоит в том, чтобы вначале оценить моменты распределения Вейбулла, приравнять их к теоретическим моментам, а затем из полученных уравнений найти параметры распределения. Фактически этот метод используется для подгонки кривых Джонсона для негауссовских распределений с целью последующего вычисления индексов пригодности (см. раздел Подгонка распределений методом моментов). Однако этот метод не подходит для обработки цензурированных наблюдений и, следовательно, для анализа времен отказов.

Сравнение методов оценивания.
Сравнение методов оценивания.

Додсон (Dodson, 1994) приводит результаты моделирования методом Монте-Карло и сравнивает различные способы оценивания. Как правило, оценки максимального правдоподобия являются лучшими для больших выборок (например, n>15), тогда как графические методы более точны для малых выборок.

Замечание об осторожном использовании доверительных интервалов, построенных методом максимального правдоподобия.


Замечание об осторожном использовании доверительных интервалов, построенных методом максимального правдоподобия.

Система STATISTICA вычисляет доверительные интервалы оценок максимального правдоподобия функции надежности, основываясь на стандартных ошибках. Додсон (Dodson, 1994) советует с осторожностью подходить к доверительным интервалам, полученным из оценок максимального правдоподобия или, более точно, оценок, при вычислении которых используется информационная матрица. Если параметр формы меньше 2, дисперсия таких оценок теряет точность и предпочтительнее использовать графические методы, основанные на непараметрических доверительных интервалах.

Критерии согласия
Критерии согласия

Имеется несколько критериев оценки качества подгонки распределения Вейбулла к данным, которые всесторонне рассматриваются в работе Lawless (1982). Мы лишь кратко перечислим эти критерии.

Критерий Холлендера-Прошана.
Критерий Холлендера-Прошана.

Этот критерий сравнивает теоретическую функцию надежности с оценкой Каплана-Майера. Точные формулы вычисления достаточно сложны и могут быть найдены в книге Dodson (1994, глава 4). Критерий Холлендера-Прошана применяется к полным, однократно или многократно цензурированным данным; однако Додсон (Dodson, 1994) отмечает слабую мощность этого критерия, например, для сильно цензурированных данных. Можно проверить нормальность распределения C статистики Холлендера-Прошана.

Критерий Манна-Шойера-Фертига.
Критерий Манна-Шойера-Фертига.

Этот критерий был предложен Манном, Шойером и Фертигом в 1973 году и описан в работах Dodson (1994) и Lawless (1982). Нулевая гипотеза предполагает, что данные имеют распределение Вейбулла с оцененными параметрами. Нельсон (Nelson, 1982) отмечает хорошую мощность этого критерия и применимость к данным с цензурированием типа II. Вычислительные детали приводятся в работах Dodson (1994) и Lawless (1982); критические значения для этой статистики вычислены методом Монте-Карло и табулированы для n (объем выборки) от 3 до 25.



Критерий Андерсона-Дарлинга.
Критерий Андерсона-Дарлинга.

Критерий Андерсона-Дарлинга позволяет сравнить эмпирическую и теоретическую функцию распределения, однако применяется он только к полным наблюдениям (без цензурирования). Критические значения статистики Андерсона-Дарлинга табулированы (см., например, Dodson, 1994, Table 4.4) для размеров выборки от 10 до 40.

Интерпретация результатов
Интерпретация результатов

При удовлетворительных результатах подгонки распределения Вейбулла к распределению времен отказов можно использовать различные графики и таблицы для исследования надежности исследуемых образцов. Если же не удалось получить хорошую подгонку распределения Вейбулла к наблюдаемым данным, то для определения формы функции надежности можно использовать независимые от распределения методы оценки параметров.

Графики функции надежности.
Графики функции надежности.

На этом графике показаны оценки функции надежности вместе с соответствующими доверительными границами.



Заметьте, что помимо стандартных могут быть вычислены и показаны на графике также и независимые от распределения, непараметрические оценки.

Графики функции риска (интенсивности отказов).
Графики функции риска (интенсивности отказов).

Как уже отмечалось, функция интенсивности или функция риска (мы используем и тот, и другой термин) описывает вероятность отказа (смерти) в малый интервал времени при условии, что в начале интервала отказа не было. График функции риска дает информацию об условной вероятности отказов.

Процентные точки функции надежности.
Процентные точки функции надежности.

Основываясь на подогнанной функции распределения Вейбулла, можно вычислить процентили функции надежности (функции выживания) вместе с доверительными границами (для оценок максимального правдоподобия). Эти оценки особенно важны для вычисления ожидаемой доли образцов, выживших к определенному моменту времени.

Группированные данные

В некоторых случаях времена отказов представляются в виде сгруппированных данных. В частности, во многих реальных исследованиях сложно оценить время отказов с достаточной точностью, но тем не менее, можно определить сколько отказов произошло или сколько наблюдений было цензурировано в течение определенного интервала времени.


Такого рода данные, так называемые таблицы жизни (отказов) обсуждаются в разделе Анализ выживаемости. Существует два основных метода подгонки распределения Вейбулла к группированным данным.

Первый подход состоит в интерполяции, т.е. в переводе таблицы в непрерывный массив данных, при этом предполагается, (1) что каждый отказ происходит в середине интервала группировки, (2) что цензурирование происходит после отказов (иными словами, цензурированные наблюдения располагаются за отказами в каждом интервале группировки). Лоулесс (Lawless, 1982) советует пользоваться данным методом в ситуациях, когда интервалы группировки относительно малы.

В другом случае вы можете рассматривать имеющиеся данные как таблицу времен жизни  и использовать для подгонки распределения Вейбулла метод взвешенных наименьших квадратов (см. Gehan and Siddiqui, 1973; Lee, 1992). В работе Lawless (1982) также описаны способы оценки параметров для группированных данных методом максимального правдоподобия.

Изменение порядка времен отказа для многократно цензурированных данных
Изменение порядка времен отказа для многократно цензурированных данных

Для многократно цензурированных данных вычисляется взвешенный ранг отказов для каждого момента, начиная с момента первого цензурирования. Затем этот новый ранг используется для вычисления медианного ранга и оценки функции распределения.

Модифицированный ранг с номером j вычисляется по формуле (см. Dodson 1994):

Oj = Op + ((n+1)-Op)/(1+c)

где:

n      - общее число наблюдений,
Op   - модифицированный ранг предыдущего наблюдения,
c      - число оставшихся точек данных , включая текущую.

При этом медианный ранг вычисляется следующим образом:

F(t) = (Oj -0.3)/(n+0.4)

где Oj - модифицированный порядок отказов, n - полное число наблюдений.

Функция распределения Вейбулла, надежность и функции риска
Функция распределения Вейбулла, надежность и функции риска

Распределение Вейбулла определено для положительных значений параметров b, c и , которые называются соответственно параметрами масштаба, формы и положения.



Плотность распределения Вейбулла:
Плотность распределения Вейбулла:

f(x) = c/b*[(x-)/b]c-1 * exp^{-[(x-)/b]c}
< x,  b > 0,  c > 0

Функция распределения (ФР) Вейбулла:
Функция распределения (ФР) Вейбулла:

F(x) = 1 - exp{-[(x-)/b]c}

Функция надежности.
Функция надежности.

Функция надежности вычисляется с помощью функции распределения Вейбулла по формуле:

R(x) = 1 - F(x)

Функция риска (интенсивности).
Функция риска (интенсивности).

Функция риска описывает вероятность отказа в течение малого промежутка времени при условии, что до этого момента отказа не произошло. На основе распределения Вейбулла получается функция риска следующего вида:

h(t) = f(t)/R(t) = [c*(x-)(c-1)] / bc

Кумулятивная функция риска:
Кумулятивная функция риска:

H(t) = (x-) / bc

В формулах для функции интенсивности и кумулятивной функции риска использованы те же обозначения, что и в приведенных выше выражениях для функций плотности и надежности.

Оглавление

(c) Copyright StatSoft, Inc., 1984-2001
STATISTICA is a trademark of StatSoft, Inc.

Анализ соответствий

Анализ соответствий
Анализ соответствий

Вводный обзор Дополнительные точки Многомерный анализ соответствий Матрица Берта

Вводный обзор
Вводный обзор

Анализ соответствий содержит описательные и разведочные методы анализа двухвходовых и многовходовых таблиц. Эти методы по своей природе похожи на методы Факторного анализа и позволяют исследовать структуру группирующих переменных, включенных в таблицу. Одной из наиболее общих разновидностей многовходовых таблиц типа являются частотные таблицы сопряженности (см., например, Основные статистики или Логлинейный анализ).

В классическом анализе соответствий частоты в таблице сопряженности стандартизуются таким образом, чтобы сумма наблюдений во всех ячейках была равна 1. Одной из целей анализа соответствий является представление содержимого таблицы относительных частот в виде расстояний между отдельными строками и/или столбцами таблицы в пространстве возможно более низкой размерности. Каким образом это достигается, лучше всего показать на простом примере, который будет рассмотрен далее. Заметим, что имеется некоторое сходство в интерпретации результатов анализа соответствий и Факторного анализа.

Для более полного описания данного метода, его вычислительных аспектов и его применения, рекомендуем классическую работу Greenacre (1984). Методы анализа соответствий впервые были разработаны во Франции Jean-Paul Benzerci в конце 1960-х - начале 1970-х годов (например, смотри Benzerci, 1973; см. также Lebart, Morineau, Tabard, 1977), однако в англо-говорящих странах они завоевали популярность сравнительно недавно (смотри, например, Carrol, Green и Schaffer, 1986; Hoffman и Franke, 1986). Заметим, что похожие методы независимо разрабатывались во многих странах и были известны под названиями: оптимальное шкалирование, взаимное усреднение, оптимальная оцифровка, квантификационный метод или анализ однородности. В последующих разделах будет представлено общее введение в анализ соответствий.

Обзор.
Обзор.

Допустим, что вы собрали данные о пристрастии к курению сотрудников некоторой компании.
Следующие данные представлены в работе Greenacre (1984, стр. 55).

Таблица 1
Таблица 1

Категории курящих   Группа
сотрудников (1)
Некурящие (2)
Слабо (3)
Средне (4)
Сильно Всего по строке (1) Старшие менеджеры
(2) Младшие менеджеры
(3) Старшие сотрудники
(4) Младшие сотрудники
(5) Секретари Всего по столбцу

4   4 25 18 10	2   3 10 24   6	3   7 12 33   7	2   4   4 13   2	11   18   51   88   25
61	45	62	25	193

Это простая двувходовая таблица. Можно считать, что 4 числа в каждой строке данной таблицы являются координатами 4-х мерного пространства, и значит, можно вычислить (евклидовы) расстояния между 5-ю точками (строками) этого 4-х мерного пространства. Расстояния между данными точками в 4-х мерном пространстве объединяют (агрегируют) всю информацию о сходствах между строками в том смысле, что чем меньше расстояние, тем больше сходство между категориями курящих. Теперь, предположим, что возможно найти пространство меньшей размерности для представления точек-строк, которое сохраняет всю или почти всю информацию о различиях между строками. В рассматриваемом случае вы можете представить всю информацию о сходстве между строками (в данном случае о типе работника) в виде 1, 2 или 3-мерного графика. Хотя это может и не быть практически полезным для маленьких таблиц, аналогичных рассматриваемой, можно себе представить, как сильно выиграет представление и интерпретация очень больших таблиц (в которых, например, записаны предпочтения для 10 потребительских товаров 100 групп респондентов) в результате упрощения, полученного путем применения методов анализа соответствий (например, представить упомянутые 10 потребительских товаров в двумерном пространстве).

Масса.
Масса.

Продолжая предыдущий пример двухвходовой таблицы, рассмотрим вычислительный аспект работы программы.


Во-первых, вычисляются относительные частоты для введенной таблицы, так что сумма всех элементов таблицы будет равна 1 (каждый элемент делится на 193 - общее число наблюдений). Полученная нормированная таблица показывает, как распределена единичная масса по ячейкам. В терминологии анализа соответствий, суммы по строкам и столбцам в матрице относительных частот называются массой строки и столбца, соответственно.

Инерция.
Инерция.

Термин инерция в анализе соответствий используется по аналогии с прикладной математикой, где понятие "момент инерции" определяется как интеграл элемента массы умноженной на квадрат расстояния до центра масс (смотри, например, Greenacre, 1984, стр.35). Инерция определяется как значение статистики хи-квадрат Пирсона для двухвходовой таблицы, деленное на общее количество наблюдений (193 в примере).

Инерция и профили строк и столбцов.
Инерция и профили строк и столбцов.

Если строки и столбцы таблицы полностью независимы друг от друга, то элементы таблицы могут быть воспроизведены исключительно при помощи сумм по строкам и столбцам или, в терминологии анализа соответствий, при помощи профилей строк и столбцов. В соответствие с известной формулой для вычисления статистики Хи-квадрат для двухвходовых таблиц, ожидаемые частоты таблицы, в которой столбцы и строки независимы, вычисляются перемножением соответствующих профилей столбцов и строк и делением полученного результата на общую сумму. Любое отклонение от ожидаемых величин (ожидаемых при гипотезе о полной независимости переменных по строкам и столбцам) будет давать вклад в совокупную статистику хи-квадрат. Таким образом, анализ соответствий можно рассматривать как метод декомпозиции статистики Хи-квадрат для двухвходовых таблиц (Инерция = Хи-квадрат/Число наблюдений) с целью определения пространства наименьшей размерности, позволяющего представить отклонения от ожидаемых величин. Это напоминает задачу Факторного анализа, где осуществляется декомпозиция совокупной вариации, так чтобы снижение размерности переменных приводило к наименьшим потерям в матрице ковариаций исходных переменных.



Анализ строк и столбцов.
Анализ строк и столбцов.

Разбор предыдущего примера начался с рассмотрения точек- строк таблицы. Однако не меньший интерес могут вызывать суммарные величины по столбцам, в этом случае можно представить точки-столбцы в пространстве меньшей размерности, которое удовлетворительно воспроизводит сходство (и расстояния) между относительными частотами для столбцов таблицы. В действительности возможно одновременное отображение на одном графике точек-столбцов и точек-строк, представляющее всю имеющуюся информацию, содержащуюся в двухвходовой таблице.

Просмотр результатов.
Просмотр результатов.

Теперь рассмотрим некоторые результаты для данной таблицы. Ниже показаны так называемые сингулярные значения, собственные значения, проценты объясненной инерции, кумулятивные проценты и вклады в статистику хи-квадрат каждого собственного значения.

Таблица 2
Таблица 2

Собственные значения и инерция для всех размерностей
Таблица ввода (Строки x Столбцы): 5 x 4
Общая инерция =.08519 Хи2=16.442 Число
измерений Сингул.
значения Собств.
значения Процент
инерции Кумул.
процент Хи-
квадрат

1 2 3	.273421 .100086 .020337	.074759 .010017 .000414	87.75587 11.75865 .48547	87.7559 99.5145 100.0000	14.42851 1.93332 .07982

Заметим, что базис в евклидовом пространстве выбирается так, чтобы расстояние между точками-строками или точками-столбцами было максимальным, и новые вектора базиса (которые независимы или ортогональны друг другу) давали все меньший и меньший вклад в величину хи-квадрат (следовательно, и величину инерции). Таким образом, процедура получения базисных векторов во многом напоминает выделение главных компонент в Факторном анализе.

Обратите внимание на то, что одна размерность, в рассматриваемом примере, объясняет 87.76% инерции, а это значит, что для рассматриваемой двухвходовой таблицы значения относительных частот, которые восстанавливаются по одной размерности, дают вклад в величину статистики Хи-квадрат (и, следовательно, инерции) в размере 87.76% от первоначального.


Две размерности позволяют объяснить 99.51% значения Хи-квадрат.

Максимальная размерность.
Максимальная размерность.

Так как частоты в таблице суммируются по строкам и по столбцам, то имеется только (число столбцов - 1) независимых элементов каждой строки и (число строк - 1) независимых элементов каждого столбца (зная значения этих элементов, вы можете заполнить оставшиеся ячейки таблицы, используя значения суммарных величин по строкам и столбцам). Следовательно, количество собственных значений, которые возможно получить для двухвходовой таблицы, равно минимум числа столбцов минус 1 и числа строк минус 1. Если используется максимальная размерность, то можно полностью восстановить всю информацию, содержащуюся в таблице.

Координаты строк и столбцов.
Координаты строк и столбцов.

Рассмотрим координаты в двумерном пространстве.

Таблица 3
Таблица 3

Имя строки Изм. 1 Изм. 2 (1) Старшие менеджеры
(2) Младшие менеджеры
(3) Старшие сотрудники
(4) Младшие сотрудники
(5) Секретари

-.065768 .258958 -.380595 .232952 -.201089	.193737 .243305 .010660 -.057744 -.078911

Вы можете отобразить на двумерной диаграмме координаты. Напомним, что целью анализа соответствий является представление расстояний между строками и/или столбцами двухвходовой таблицы в пространстве меньшей размерности. Также заметим, что, как и в Факторном анализе, ориентация векторов базиса выбрана таким образом, что каждый новый базисный вектор "объяснял" все меньше и меньше величину статистики Хи-квадрат (или инерции). Вы, например, можете изменить знаки всех столбцов предыдущей таблицы и повернуть, таким образом, оси на 180°.

Важным преимуществом двумерного пространства является то, что точки-строки, отображаемые в виде точек, которые находятся в непосредственной близости друг от друга, близки и по относительным частотам. Если вы построили данную диаграмму, то, рассматривая расположение точек по первой оси, обратите внимание на то, что Старшие сотрудники и Секретари относительно близки по координатам.


Если же посмотреть на строки таблицы относительных частот (частоты стандартизованы так, что их сумма по каждой строке равна 100%), то сходство для данных двух групп по категориям интенсивности курения становится очевидным.

Таблица 4
Таблица 4

Проценты по строке Категории курящих   Группа
сотрудников (1)
Некурящие (2)
Слабо (3)
Средне (4)
Сильно Всего по
строке (1) Старшие менеджеры
(2) Младшие менеджеры
(3) Старшие сотрудники
(4) Младшие сотрудники
(5) Секретари

36.36 22.22 49.02 20.45 40.00	18.18 16.67 19.61 27.27 24.00	27.27 38.89 23.53 37.50 28.00	18.18 22.22   7.84 14.77   8.00	100.00 100.00 100.00 100.00 100.00

Очевидно, что окончательной целью анализа соответствий является теоретическая интерпретация векторов в полученном пространстве более низкой размерности. Одним из способов, который может помочь в интерпретации полученных результатов, является представление на диаграмме точек-столбцов. В следующей таблице показаны координаты точек-столбцов:

Таблица 5
Таблица 5

Категория
курящих  
Изм. 1  
Изм. 2 Некурящие
Слабо
Средне
Сильно

-.393308 .099456 .196321 .293776	.030492 -.141064 -.007359 .197766

Можно сказать, что первая размерность дает отличие между градациями интенсивности курения, в данном случае между категориями Некурящие и все остальные. Следовательно, можно объяснить большую степень сходства между Старшими менеджерами и Секретарями, о которой уже шла речь выше, наличием в данных группах большого количества Некурящих.

Совместимость координат строк и столбцов.
Совместимость координат строк и столбцов.

Имеется возможность для отображения координат по строкам и столбцам на одной диаграмме. Однако важно помнить, что на таких диаграммах нужно интерпретировать сходства и различия между точками-строками и точками-столбцами отдельно по строкам и отдельно по столбцам, совместная интерпретация не имеет смысла.



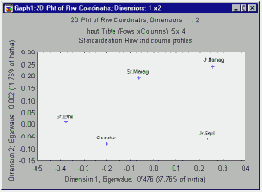
В данном примере было бы неправильно сказать, что категория Некурящие имеет сходство с категорией Старшие сотрудники (эти две точки очень близки на совместной диаграмме).


Однако, как уже отмечалось ранее, возможно делать общие замечания о природе имеющихся координат, базируясь на положении рассматриваемых точек относительно начала координат. Например, так как категория Некурящие является единственной точкой-столбцом, расположенной слева от начала координат по первой оси, и категория Старшие сотрудники также попадает туда же, то можно сказать, что первая ось отделяет категорию Некурящих от остальных, и что категория Старшие сотрудники отличается, например, от категории Младшие сотрудники тем, что в ней имеется относительно большее число некурящих сотрудников.

Шкалирование координат (возможности стандартизации).
Шкалирование координат (возможности стандартизации).

Еще одним важным решением, которое принимает аналитик, является решение о шкалировании координат. Решение о выборе той или иной опции зависит от того, собираетесь ли вы анализировать относительные проценты по рядам, по столбцам или по тем и другим одновременно. В контексте предыдущего примера, проценты по рядам сравнивались для того, чтобы проиллюстрировать наблюдаемое сходство процентов в таблице для близких точек на диаграмме. Другими словами, координаты точек прямо связаны с анализом матрицы профилей строк, в которой сумма элементов строки равна 1 (каждый элемент rij в матрице профилей строк интерпретируется как условная вероятность того, что элемент i-й строки принадлежит столбцу j). Таким образом, координаты вычисляются так, чтобы максимизировать расстояние между профилями строк (процентов по строкам). Координаты строк вычисляются по матрице профилей строк, а координаты столбцов вычисляются по матрице профилей столбцов.

Имеется также опция Канонической стандартизации (см. Gifi, 1981), эта разновидность стандартизации применяется к столбцам и строкам матрицы относительных частот. Данная стандартизация применяется для шкалирования стандартизаций профилей по строкам и столбцам и не является широко распространенной. Отметим, что существует возможность задавать собственную стандартизацию по выбору пользователя, если имеются значения собственных значений и собственных векторов.



Метрика координатной системы.
Метрика координатной системы.

Во введении термин расстояние также использовался для обозначения различий между строками и столбцами матрицы относительных частот, которые, в свою очередь, представлялись в пространстве меньшей размерности в результате использования методов анализа соответствий. В действительности, расстояния представленные в виде координат в пространстве соответствующей размерности это не просто евклидовы расстояния, вычисленные по относительным частотам столбцов и строк, а некоторые взвешенные расстояния. Процедура подбора весов устроена таким образом, чтобы в пространстве более низкой размерности метрикой являлась бы метрика Хи-квадрат, учитывая, что вы сравниваете точки-строки и выбираете стандартизацию профилей строк или стандартизацию профилей строк и столбцов или что вы сравниваете точки-столбцы и выбираете стандартизацию профилей столбцов или стандартизацию профилей строк и столбцов.

В этом случае (но не в случае канонической стандартизации) возведенное в квадрат евклидово расстояние между, например, двумя точками-строками i и i' в некоторой координатной системе соответствующей размерности аппроксимируют взвешенное (например, Хи-квадрат) расстояние между относительными частотами (см. Hoffman и Franke, формула 21):

dii '2 = j (1/cj (pij /ri - p2i ' j /ri '))

В данной формуле dii '2 - квадрат расстояния между двумя точками, cj - сумма по всем элементам в столбце j стандартизованной частотной таблицы (в которой сумма по всем элементам или масса равна 1), pij - элемент стандартизованной частотной таблицы (строка i, столбец j), ri - сумма по всем элементам в строке i таблицы относительных частот, оператор суммирует по столбцам таблицы. Другими словами, только расстояния между точками-строками и, соответственно, между точками-столбцами могут интерпретироваться в подобной манере, однако расстояния между строками и столбцами такой интерпретации не подлежат.

Оценка качества решения.
Оценка качества решения.

Имеется также некоторые дополнительные статистики, помогающие интерпретировать качество найденного решения.


Все ( или большинство) точки должны быть правильно представлены, т.е. расстояния между ними в результате применения процедуры анализа соответствий не должны искажаться. В следующей таблице представлены результаты вычисления статистик по имеющимся координатам строк, основанные только на одномерном решении в предыдущем примере (т.е. только одно измерение использовалось для восстановления профилей строк матрицы относительных частот).

Таблица 6
Таблица 6

Координаты и вклад в инерцию строки Группа
сотрудников Коорд.
Изм.1
Масса  
Качкство Относит.
инерция Инерция
Изм.1 Косинус2
Изм.1 (1) Старшие менеджеры
(2) Младшие менеджеры
(3) Старшие сотрудники
(4) Младшие сотрудники
(5) Секретари

-.065768 .258958 -.380595 .232952 -.201089	.056995 .093264 .264249 .455959 .129534	.092232 .526400 .999033 .941934 .865346	.031376 .139467 .449750 .308354 .071053	.003298 .083659 .512006 .330974 .070064	.092232 .526400 .999033 .941934 .865346

Координаты.
Координаты.

Первый столбец данной таблицы результатов содержит координаты, интерпретация которых, как мы уже отмечали, зависит от выбранной стандартизации. Размерность выбирается пользователем (в данном примере мы выбрали одномерное пространство), и координаты отображаются для каждого измерения (т.е. отображается по одному столбцу координат на каждую ось).

Масса.
Масса.

Столбец Масса содержит суммы всех элементов для каждой строки матрицы относительных частот (т.е. для матрицы, где каждый элемент содержит соответствующую массу, как уже упоминалось выше). Напомним, координаты вычисляются на основе матрицы условных вероятностей, представленной в столбце Масса.

Качество.
Качество.

Столбец Качество содержит информацию о качестве представления соответствующей точки-строки в координатной системе, определяемой выбранной размерностью. В рассматриваемой таблице было выбрано только одно измерение, поэтому числа в столбце качество являются качеством представления результатов в одномерном пространстве.


Повторим еще раз, что в вычислительном плане целью анализа соответствий является представление расстояний между точками в пространстве более низкой размерности. Если вы используете максимальную размерность (равную минимуму числа строк и столбцов минус один), то вы можете воспроизвести все расстояния в точности. Качество точки определяется как отношение квадрата расстояния - от данной точки до начала координат в пространстве выбранной размерности - к квадрату расстояния до начала координат, определенному в пространстве максимальной размерности (помните, что в качестве метрики в этом случае выбрана метрика Хи-квадрат, как уже упоминалось ранее). По аналогии с Факторным анализом качество точки похоже по интерпретации на показатель общности переменной в факторном анализе.

Заметим, что величина качества не зависит от выбранного метода стандартизации и всегда использует стандартизацию, установленную по умолчанию (т.е. метрикой расстояния является Хи-квадрат, и мера качества может интерпретироваться как доля Хи-квадрат, определяемая соответствующей строкой в пространстве соответствующей размерности). Низкое качество означает, что имеющееся число измерений недостаточно хорошо представляет соответствующую строку (столбец). В предыдущей таблице качество для первой строки (Старшие менеджеры) меньше 0.1, и это говорит о том, что данная точка плохо представлена в пространстве размерности единица.

Относительная инерция.
Относительная инерция.

Качество точки (см. выше) представляет отношение вклада данной точки в общую инерцию (Хи-квадрат), что может объяснять выбранную размерность. Однако, качество не отвечает на вопрос насколько, в действительности, и в каких размерах соответствующая точка вносит вклад в инерцию (величину Хи-квадрат). Относительная инерция представляет долю общей инерции, принадлежащую данной точке, и не зависит от выбранной пользователем размерности. Отметим, что какое-либо частное решение может достаточно хорошо представлять точку (высокое качество), но та же точка может вносить очень малый вклад в общую инерцию (т.е.


точка-строка, элементами которой являются относительные частоты, имеет сходство с некоторой строкой, элементы которой представляют собой среднее по всем строкам).

Относительная инерция для каждой размерности.
Относительная инерция для каждой размерности.

Данный столбец содержит относительный вклад соответствующей точки-строки в величину инерции, обусловленный соответствующей размерностью. В отчете данная величина приводится для каждой точки (строки или столбца) и для каждого измерения.

Косинус2 (качество или квадратичные корреляции с каждой размерностью).
Косинус2 (качество или квадратичные корреляции с каждой размерностью).

Данный столбец содержит качество для каждой точки, обусловленное соответствующей размерностью. Если просуммировать построчно элементы этих столбцов для каждой размерности, то в результате получим столбец величин Качество, о которых уже упоминалось выше (так как в рассматриваемом примере была выбрана размерность 1, то столбец Косинус2 совпадает со столбцом Качество). Эта величина может интерпретироваться как "корреляция" между соответствующей точкой и соответствующей размерностью. Термин Косинус2 возник по причине того, что данная величина является квадратом косинуса угла, образованного данной точкой и соответствующей осью (см. Greenacre, 1984, для детального анализа геометрической интерпретации анализа соответствий).

Замечание о "статистической значимости".
Замечание о "статистической значимости".

Необходимо отметить, что анализ соответствий является разведочным методом. Данный метод был разработан на базе методологии, рассматривающей построение моделей с точки зрения их соответствия данным, а не наоборот ("второй принцип" Benzerci постулирует так: "Модель должна удовлетворять имеющимся данным, а не наоборот"; см. Greenacre, 1984, стр.10). Следовательно, не существует статистических тестов, которые могли бы быть использованы для проверки результатов анализа соответствий. Главной целью анализа соответствий является представление в упрощенном виде (пространстве меньшей размерности) информации, содержащейся в больших частотных таблицах (или таблицах с аналогичными мерами соответствия).

В начало

Дополнительные точки
Дополнительные точки

Во Вводном обзоре описано, как интерпретировать координаты и связанные с ними статистики. Дополнительную помощь в интерпретации результатов может оказать включение дополнительных точек-строк или столбцов, которые на первоначальном этапе не участвовали в анализе. Например, рассмотрим следующие результаты, основанные на примере, использованном в водном разделе (см. также работу Greenacre, 1984).

Таблица 7
Таблица 7

Имя строки Изм. 1 Изм. 2 (1) Старшие менеджеры
(2) Младшие менеджеры
(3) Старшие сотрудники
(4) Младшие сотрудники
(5) Секретари Национальное среднее

-.065768 .258958 -.380595 .232952 -.201089	.193737 .243305 .010660 -.057744 -.078911
-.258368	-.117648

Данная таблица отображает координаты (для двух размерностей), вычисленные для таблицы частот, состоящей из классификации степени пристрастия к курению среди сотрудников различных должностей. Строка Национальное среднее содержит координаты дополнительной точки, которая является национальным средним уровнем (в процентах) по различным категориям курящих (Национальное среднее - среднее для разных национальностей курящих, вымышленные цифры, приведенные в Greenacre, 1984, таковы: Некурящие - 42%, легко курящие - 29%, средне курящие - 20%, сильно курящие - 9%). Если вы построите двумерную диаграмму групп сотрудников и Национального среднего, то сразу убедитесь в том, что данная дополнительная точка и группа Секретари очень близки друг к другу и по одну сторону горизонтальной оси координат с категорией Некурящие (точкой-столбцом). Другими словами, выборка представленная в исходной частотной таблице содержит больше курящих, чем Национальное среднее.

Хотя такое же заключение можно сделать, взглянув на исходную таблицу сопряженности, в таблицах больших размеров подобные выводы, конечно, не столь очевидны.

Качество представления дополнительных точек.
Качество представления дополнительных точек.

Еще одним интересным результатом, касающимся дополнительных точек, является интерпретация качества, представления при заданной размерности (см. Вводный обзор для более подробного обсуждения концепции качества представления).


Повторим еще раз, что целью анализа соответствий является представление расстояний между координатами строк или столбцов в пространстве более низкой размерности. Зная, как решается данная задача, необходимо ответить на вопрос, является ли адекватным (в смысле расстояний до точек в исходном пространстве) представление дополнительной точки в пространстве выбранной размерности. Ниже представлены статистики для исходных точек и для дополнительной точки Национальное среднее для задачи в двумерном пространстве.

Таблица 8
Таблица 8

Группа
сотрудников
Качество Косин2
Изм.1 Косин2
Изм.2 (1) Старшие менеджеры
(2) Младшие менеджеры
(3) Старшие сотрудники
(4) Младшие сотрудники
(5) Секретари Национальное среднее

.892568 .991082 .999817 .999810 .998603	.092232 .526400 .999033 .941934 .865346	.800336 .464682 .000784 .057876 .133257
.761324	.630578	.130746

Все вышеперечисленные статистики уже обсуждались в вводном обзоре. Напомним, что качество точек-строк или столбцов определено, как отношение квадрата расстояния от точки до начала координат, в пространстве сниженной размерности, к квадрату расстояния от точки до начала координат, в исходном пространстве (помните, что в качестве метрики выбирается расстояние Хи-квадрат). В определенном смысле, качество является величиной, объясняющей долю квадрата расстояния до центра масс. Дополнительная точка-строка Национальное среднее имеет качество, равное .76, это означает, что данная точка достаточно хорошо представлена в двумерном пространстве. Статистика Косинус**2 - это качество представления соответствующей точки-строки, обусловленное выбором пространства заданной размерности (если просуммировать построчно элементы столбцов Косинус2 для каждого измерения, то в результате получим столбец величин Качество).

В начало

  Многомерный анализ соответствий (МАС)
Многомерный анализ соответствий (МАС)

Многомерный Анализ Соответствий (МАС) можно рассматривать как обобщение анализа соответствий на случай более одной размерности.


Для ознакомления с анализом соответствий обратитесь к разделу Вводный обзор. Многомерный анализ соответствий - это анализ соответствий на бинарной (индикаторной) матрице, где объекты расположены по строкам, а группирующие переменные по столбцам. Обычно в анализе используется не матрица в бинарной форме, а матрица Берта (Burt), которая получается в результате матричного умножения транспонированной матрицы на исходную бинарную матрицу. Однако для простоты интерпретации результатов многомерного анализа соответствий, мы будем обсуждать применение анализа соответствий на примере бинарной матрицы.

Бинарная или индикаторная матрица.
Бинарная или индикаторная матрица.

Рассмотрим пример простой двухвходовой матрицы, рассмотренный во вводном обзоре.

Таблица 9
Таблица 9

Категории курящих   Группа
сотрудников (1)
Некурящие (2)
Слабо (3)
Средне (4)
Сильно Всего по строке (1) Старшие менеджеры
(2) Младшие менеджеры
(3) Старшие сотрудники
(4) Младшие сотрудники
(5) Секретари Всего по столбцу

4   4 25 18 10	2   3 10 24   6	3   7 12 33   7	2   4   4 13   2	11   18   51   88   25
61	45	62	25	193

Допустим, что вы представили эти данные в виде бинарной матрицы.

Таблица 10
Таблица 10

  Группа сотрудников Курящие Номер
наблюдения Старший
менеджер Младший
менеджер Старший
сотрудник Младший
сотрудник  
Секретарь  
Некурящий  
Слабо  
Средне  
Сильно 1
2
3
4
5
...
...
...
191
192
193

1 1 1 1 1 . . . 0 0 0	0 0 0 0 0 . . . 0 0 0	0 0 0 0 0 . . . 0 0 0	0 0 0 0 0 . . . 0 0 0	0 0 0 0 0 . . . 1 1 1	1 1 1 1 0 . . . 0 0 0	0 0 0 0 1 . . . 0 0 0	0 0 0 0 0 . . . 1 0 0	0 0 0 0 0 . . . 0 1 1

Каждый из 193 объектов записан в этой матрице.


Если объект принадлежит некоторой категории, то элемент на пересечении соответствующей строки и столбца равен 1, в противном случае 0. Например, объект 1 представляет Старшего менеджера, который принадлежит категории Некурящие. Как легко определить по исходной двухвходовой матрице, всего имеется 4 таких наблюдения, и, следовательно, имеется четыре объекта в бинарной матрице.

Анализ бинарной матрицы.
Анализ бинарной матрицы.

Если бы вы анализировали рассматриваемый файл (бинарную матрицу) как двухвходовую таблицу, то в качестве результатов получили бы столбцы координат, которые позволили бы связать различные категории друг с другом, основываясь на расстояниях между точками-строками, т.е. между индивидуальными объектами. В действительности, вид столбцов координат был бы очень похож на столбцы координат, получаемые в результате применения анализа соответствий к двухвходовой частотной таблице (заметим, что метрики в рассматриваемых пространствах будут различны, однако, относительное расположение точек схоже).

Более чем две переменных.
Более чем две переменных.

Подход, который мы наметили, для анализа группированных данных, можно легко распространить на случай более двух переменных. Например, бинарная матрица может дополнительно включать переменные Мужчина и Женщина, которые аналогично кодируются 0 или 1, или еще три переменные обуславливающие принадлежность к той или иной возрастной группе. Таким образом, окончательный результат может представлять взаимосвязи между переменными Пол, Возраст, Склонность к курению и Занимаемая должность (Группа сотрудников).

Нечеткое кодирование.
Нечеткое кодирование.

Каждый объект не обязательно должен принадлежать какой-либо одной категории рассматриваемой категоризованной переменной. Помимо кодировки 0 или 1, возможно ввести вероятностное распределение на категориях переменной или какую-либо другую меру, реализующую нечеткое правило для принадлежности к той или иной группе. Greenacre (1984) в своей работе рассмотрел различные схемы такого кодирования.


Например, допустим, что в рассмотренной выше бинарной матрице, имеются пропущенные данные, относящиеся к типам курящих. Вместо исключения попущенных данных из анализа (или создания новой категории Пропущенные данные), вы можете приписать данным пропущенным категориям некоторые числа (дающие в сумме 1), интерпретируемые как вероятности того, что соответствующий объект попадает в данную категорию (например, вы можете приписывать вероятности, основываясь на информации об оценках средних величин для всего населения по категориям).

Интерпретация координат и другие результаты.
Интерпретация координат и другие результаты.

Повторим, что результаты, полученные методом многомерного анализа соответствий для координат точек, идентичны результатам применения анализа соответствий к бинарной матрице. Следовательно, интерпретация координат, качества, квадратов косинусов и других статистик анализа соответствий полностью переносится на случай многомерного анализа соответствий (см. Вводный обзор), заметим только, что вышеперечисленные статистики, в случае многомерного анализа соответствий, относятся к инерции всей бинарной матрицы.

Дополнительные точки-столбцы и "множественная регрессия" группирующих переменных.
Дополнительные точки-столбцы и "множественная регрессия" группирующих переменных.

Еще одним применением бинарных матриц служит возможность применения метода, эквивалентного методу Множественной регрессии для группирующих переменных путем добавления дополнительных точек-столбцов к бинарной матрице. Например, предположим, что вы добавили к бинарной матрице еще два столбца, чтобы ответить на вопрос, болел или нет опрашиваемый в течение прошедшего года (т.е. вы добавляете столбец с именем Болен и столбец с именем Не болен и, как обычно, используете 1 или 0 для обозначения принадлежности к той или иной категории). Применяя анализ соответствий для рассматриваемой бинарной матрицы, во-первых, вы можете объяснить влияние других показателей на показатель заболеваемости с помощью качества представления (см. Вводный обзор), и, во-вторых, отображение координат дополнительных точек может указать природу (направление) зависимостей между столбцами бинарной матрицы и столбцами дополнительных точек, отражающими заболеваемость.


Добавление дополнительных точек в МАС анализ иногда называют предсказывающим отображением.

Матрица Берта. Реальные вычисления в многомерном анализе соответствий не используют индикаторную матрицу (которая может быть очень большой, если рассматривается много объектов и переменных). Для вычислений используется матричное произведение транспонированной и исходной бинарной матрицы или матрица Берта. Данная квадратная матрица табулирует связи между всеми имеющимися категориям. Для двухвходовой таблицы, рассмотренной ранее, матрица Берта имеет следующий вид:

Таблица 11
Таблица 11

Сотрудники Курящие (1) (2) (3) (4) (5) (1) (2) (3) (4) (1) Старшие менеджеры
(2) Младшие менеджеры
(3) Старшие сотрудники
(4) Младшие сотрудники
(5) Секретари
(1) Курящие:Нет
(2) Курящие:Слабо
(3) Курящие:Средне
(4) Курящие:Сильно

11 0 0 0 0 4 2 3 2	0 18 0 0 0 4 3 7 4	0 0 51 0 0 25 10 12 4	0 0 0 88 0 18 24 33 13	0 0 0 0 25 10 6 7 2	4 4 25 18 10 61 0 0 0	2 3 10 24 6 0 45 0 0	3 7 12 33 7 0 0 62 0	2 4 4 13 2 0 0 0 25

Матрица Берта имеет достаточно очевидную структуру. В случае двух группирующих переменных (как показано выше), матрица Берта состоит из четырех блоков: подматрица кросстабуляции переменной Сотрудники с переменной Сотрудники, подматрица кросстабуляции переменной Сотрудники с переменной Курящие, подматрица кросстабуляции переменной Курящие с переменной Сотрудники и подматрица кросстабуляции переменной Курящие с переменной Курящие. Заметим, что данная матрица симметрична и что суммы диагональных элементов в каждом блоке, представляющем кросстабуляцию некоторой переменной с собой, равны (например, в данном примере размер выборки был равен 193, и, следовательно, суммы диагональных элементов подматриц кросстабуляции переменных Сотрудники с собой и Курящие с собой эквивалентны и равны 193).

Внедиагональные элементы подматриц, представляющих кросстабуляцию переменных с собой, равны 0. Однако это не является правилом, например, когда матрица Берта получена из бинарной матрицы, включающей нечеткое кодирование принадлежности категории (см.


выше), в этом случае внедиагональные элементы могут отличаться от 0.

В начало

  Матрица Берта
Матрица Берта

Многомерный анализ соответствий использует в качестве входного формата данных (т.е. преобразует произвольные данные к такому формату) матрицу Берта. Матрица Берта является квадратом бинарной матрицы, поэтому результаты применения многомерного анализа соответствий аналогичны результатам анализа соответствий для точек-столбцов бинарной матрицы (см. также раздел МАС).

Например, допустим, что вы ввели данные по выживанию различных возрастных групп в различных городах.

Таблица 12
Таблица 12

ВЫЖИЛ ВОЗРАСТ ГОРОД Номер набл. НЕТ ДА ДО50 ОТ50ДО69 ПОСЛЕ69 ТОКИО БОСТОН МИЛАН 1
2
3
4
...
...
...
762
763
764

0 1 0 0 . . . 1 0 0	1 0 1 1 . . . 0 1 1	0 1 0 0 . . . 0 1 0	1 0 1 0 . . . 1 0 1	0 0 0 1 . . . 0 0 0	0 1 0 0 . . . 1 0 0	0 0 1 0 . . . 0 1 0	1 0 0 1 . . . 0 0 1

В данной таблице 1 обозначает, что данный субъект принадлежит соответствующему множеству категорий (например, Выжил имеет категории Да и Нет). Например, первый субъект выжил (т.к. 0 находится в категории Нет, 1 в категории Да), в том же случае, субъект находится в возрасте от 50 до 69 лет (1 установлена в категории От50до60) и проживает в Милане. Выборка состоит из 764 субъектов.

Если вы обозначите данные (бинарную матрицу) в рассматриваемом примере как матрица X, то матричное произведение X'X является матрицей Берта. Ниже приведена матрица Берта для данного примера.

Таблица 13
Таблица 13

  ВЫЖИЛ ВОЗРАСТ ГОРОД НЕТ ДА <50 50-69 69+ ТОКИО БОСТОН МИЛАН ВЫЖИЛ:НЕТ
ВЫЖИЛ:ДА
 
ВОЗРАСТ:ДО50
ВОЗРАСТ:ОТ50ДО69
ВОЗРАСТ:ПОСЛЕ69 

ГОРОД:ТОКИО
ГОРОД:БОСТОН
ГОРОД:МИЛАН

210 0   68 93 49   60 82 68	0 554   212 258 84   230 171 153	68 212   280 0 0   151 58 71	93 258   0 351 0   120 122 109	49 84   0 0 133   19 73 41	60 230   151 120   19   290     0     0	82 171     58 122   73       0 253     0	68 153     71 109   41       0     0 221

Структура рассматриваемой матрицы Берта очевидна. Данная матрица симметрична. В случае 3 группирующих переменных (как в рассматриваемом примере) матрица данных состоит из 3 x 3 = 9 блоков, которые образуются в результате взаимной кросстабуляции имеющихся группирующих переменных. Заметим, что суммы диагональных элементов каждого диагонального блока (т.е. в тех блоках, где переменные кросстабулированы сами с собой) постоянны и равны 764 для данного случая.

Все внедиагональные элементы, принадлежащие диагональным блокам, равны 0. Если же объекты некоторой бинарной матрицы кодировались с помощью процедуры нечеткого кодирования (т.е. если принадлежность объекта категории определялась некоторой вероятностью), то равенство 0 внедиагональных элементов диагональных блоков не гарантировано.

В начало

(c) Copyright StatSoft, Inc., 1984-2001
STATISTICA является торговой маркой StatSoft, Inc.

Анализ временных рядов

Анализ временных рядов
Анализ временных рядов

Общее введение Две основные цели Идентификация модели временных рядов Систематическая составляющая и случайный шум Два общих типа компонент временных рядов Анализ тренда Анализ сезонности АРПСС (Бокс и Дженкинс) и автокорреляции Общее введение Два основных процесса Модель АРПСС Идентификация Оценивание параметров Оценивание модели Прерванные временные ряды Экспоненциальное сглаживание Общее введение Простое экспоненциальное сглаживание Выбор лучшего значения параметра a (альфа) Индексы качества подгонки Сезонная и несезонная модели с трендом или без тренда Сезонная декомпозиция (метод Census I) Общее введение Вычисления Сезонная корректировка X-11 (метод Census II) Сезонная корректировка: основные идеи и термины Метод Census II Таблицы результатов корректировки X-11 Подробное описание всех таблиц результатов, вычисляемых в методе X-11 Анализ распределенных лагов Общая цель Общая модель Распределенный лаг Алмона Одномерный анализ Фурье Кросс-спектральный анализ Общее введение Основные понятия и принципы Результаты для каждой переменной Кросс-периодограмма, кросс-плотность, квадратурная плотность и кросс-амплитуда Квадрат когерентности, усиление и фазовый сдвиг Как создавались данные для примера Спектральный анализ - Основные понятия и принципы Частота и период Общая структура модели Простой пример Периодограмма Проблема рассеяния Добавление констант во временной ряд (пэддинг) Косинус-сглаживание Окна данных и оценки спектральной плотности Подготовка данных к анализу Результаты для случая, когда в ряде отсутствует периодичность Быстрое преобразование Фурье Общее введение Вычисление БПФ во временных рядах

В следующих разделах мы вначале представим обзор методов, используемых для идентификации моделей временных рядов (таких как сглаживание, подгонка и автокорреляции). Затем опишем общий класс моделей, которые могут быть использованы для описания рядов и построения прогнозов (модели авторегрессии и скользящего среднего).
Наконец, расскажем о некоторых простых, но часто используемых методах, основанных на линейной регрессии. За дальнейшей информацией обратитесь к соответствующим разделам.

Общее введение

Вначале дадим краткий обзор методов анализа данных, представленных в виде временных рядов, т.е. в виде последовательностей измерений, упорядоченных в неслучайные моменты времени. В отличие от анализа случайных выборок, анализ временных рядов основывается на предположении, что последовательные значения в файле данных наблюдаются через равные промежутки времени (тогда как в других методах нам не важна и часто не интересна привязка наблюдений ко времени).

Подробное обсуждение этих методов можно найти в следующих работах: Anderson (1976), Бокс и Дженкинс (1976), Kendall (1984), Kendall and Ord (1990), Montgomery, Johnson, and Gardiner (1990), Pankratz (1983), Shumway (1988), Vandaele (1983), Walker (1991), Wei (1989).

  Две основные цели

Существуют две основные цели анализа временных рядов: (1) определение природы ряда и (2) прогнозирование (предсказание будущих значений временного ряда по настоящим и прошлым значениям). Обе эти цели требуют, чтобы модель ряда была идентифицирована и, более или менее, формально описана. Как только модель определена, вы можете с ее помощью интерпретировать рассматриваемые данные (например, использовать в вашей теории для понимания сезонного изменения цен на товары, если занимаетесь экономикой). Не обращая внимания на глубину понимания и справедливость теории, вы можете экстраполировать затем ряд на основе найденной модели, т.е. предсказать его будущие значения.

В начало

  Идентификация модели временных рядов Систематическая составляющая и случайный шум Два общих типа компонент временных рядов Анализ тренда Анализ сезонности За более полной информацией о простых автокорреляциях (обсуждаемых в этом разделе) и других автокорреляциях, см. Anderson (1976), Box and Jenkins (1976), Kendall (1984), Pankratz (1983), and Vandaele (1983). См. также: АРПСС (Бокс и Дженкинс) и автокорреляции Прерванные временные ряды Экспоненциальное сглаживание Сезонная декомпозиция (метод Census I) Сезонная корректировка X-11 (метод Census II) Таблицы результатов корректировки X-11 Анализ распределенных лагов Одномерный анализ Фурье Кросс-спектральный анализ Основные понятия и принципы Быстрое преобразование Фурье   Систематическая составляющая и случайный шум


Систематическая составляющая и случайный шум

Как и большинство других видов анализа, анализ временных рядов предполагает, что данные содержат систематическую составляющую (обычно включающую несколько компонент) и случайный шум (ошибку), который затрудняет обнаружение регулярных компонент. Большинство методов исследования временных рядов включает различные способы фильтрации шума, позволяющие увидеть регулярную составляющую более отчетливо.

  Два общих типа компонент временных рядов
Два общих типа компонент временных рядов

Большинство регулярных составляющих временных рядов принадлежит к двум классам: они являются либо трендом, либо сезонной составляющей. Тренд представляет собой общую систематическую линейную или нелинейную компоненту, которая может изменяться во времени. Сезонная составляющая - это периодически повторяющаяся компонента. Оба эти вида регулярных компонент часто присутствуют в ряде одновременно. Например, продажи компании могут возрастать из года в год, но они также содержат сезонную составляющую (как правило, 25% годовых продаж приходится на декабрь и только 4% на август).



Эту общую модель можно понять на "классическом" ряде - Ряд G (Бокс и Дженкинс, 1976, стр. 531), представляющем месячные международные авиаперевозки (в тысячах) в течение 12 лет с 1949 по 1960 (см. файл Series_g.sta). График месячных перевозок ясно показывает почти линейный тренд, т.е. имеется устойчивый рост перевозок из года в год (примерно в 4 раза больше пассажиров перевезено в 1960 году, чем в 1949). В то же время характер месячных перевозок повторяется, они имеют почти один и тот же характер в каждом годовом периоде (например, перевозок больше в отпускные периоды, чем в другие месяцы). Этот пример показывает довольно определенный тип модели временного ряда, в которой амплитуда сезонных изменений увеличивается вместе с трендом. Такого рода модели называются моделями с мультипликативной сезонностью.

Анализ тренда
Анализ тренда

Не существует "автоматического" способа обнаружения тренда в временном ряде.


Однако если тренд является монотонным (устойчиво возрастает или устойчиво убывает), то анализировать такой ряд обычно нетрудно. Если временные ряды содержат значительную ошибку, то первым шагом выделения тренда является сглаживание.

Сглаживание.
Сглаживание.

Сглаживание всегда включает некоторый способ локального усреднения данных, при котором несистематические компоненты взаимно погашают друг друга. Самый общий метод сглаживания - скользящее среднее, в котором каждый член ряда заменяется простым или взвешенным средним n соседних членов, где n - ширина "окна" (см. Бокс и Дженкинс, 1976; Velleman and Hoaglin, 1981). Вместо среднего можно использовать медиану значений, попавших в окно. Основное преимущество медианного сглаживания, в сравнении со сглаживанием скользящим средним, состоит в том, что результаты становятся более устойчивыми к выбросам (имеющимся внутри окна). Таким образом, если в данных имеются выбросы (связанные, например, с ошибками измерений), то сглаживание медианой обычно приводит к более гладким или, по крайней мере, более "надежным" кривым, по сравнению со скользящим средним с тем же самым окном. Основной недостаток медианного сглаживания в том, что при отсутствии явных выбросов, он приводит к более "зубчатым" кривым (чем сглаживание скользящим средним) и не позволяет использовать веса.

Относительно реже, когда ошибка измерения очень большая, используется метод сглаживания методом наименьших квадратов, взвешенных относительно расстояния или метод отрицательного экспоненциально взвешенного сглаживания. Все эти методы отфильтровывают шум и преобразуют данные в относительно гладкую кривую (см. соответствующие разделы, где каждый из этих методов описан более подробно). Ряды с относительно небольшим количеством наблюдений и систематическим расположением точек могут быть сглажены с помощью бикубических сплайнов.

Подгонка функции.
Подгонка функции.

Многие монотонные временные ряды можно хорошо приблизить линейной функцией.


Если же имеется явная монотонная нелинейная компонента, то данные вначале следует преобразовать, чтобы устранить нелинейность. Обычно для этого используют логарифмическое, экспоненциальное или (менее часто) полиномиальное преобразование данных.

Анализ сезонности
Анализ сезонности

Периодическая и сезонная зависимость (сезонность) представляет собой другой общий тип компонент временного ряда. Это понятие было проиллюстрировано ранее на примере авиаперевозок пассажиров. Можно легко видеть, что каждое наблюдение очень похоже на соседнее; дополнительно, имеется повторяющаяся сезонная составляющая, это означает, что каждое наблюдение также похоже на наблюдение, имевшееся в том же самом месяце год назад. В общем, периодическая зависимость может быть формально определена как корреляционная зависимость порядка k между каждым i-м элементом ряда и (i-k)-м элементом (Kendall, 1976). Ее можно измерить с помощью автокорреляции (т.е. корреляции между самими членами ряда); k обычно называют лагом (иногда используют эквивалентные термины: сдвиг, запаздывание). Если ошибка измерения не слишком большая, то сезонность можно определить визуально, рассматривая поведение членов ряда через каждые k временных единиц.

Автокорреляционная коррелограмма.
Автокорреляционная коррелограмма.

Сезонные составляющие временного ряда могут быть найдены с помощью коррелограммы. Коррелограмма (автокоррелограмма) показывает численно и графически автокорреляционную функцию (AКФ), иными словами коэффициенты автокорреляции (и их стандартные ошибки) для последовательности лагов из определенного диапазона (например, от 1 до 30). На коррелограмме обычно отмечается диапазон в размере двух стандартных ошибок на каждом лаге, однако обычно величина автокорреляции более интересна, чем ее надежность, потому что интерес в основном представляют очень сильные (а, следовательно, высоко значимые) автокорреляции (см. Элементарные понятия статистики).

Исследование коррелограмм.
Исследование коррелограмм.

При изучении коррелограмм следует помнить, что автокорреляции последовательных лагов формально зависимы между собой.


Рассмотрим следующий пример. Если первый член ряда тесно связан со вторым, а второй с третьим, то первый элемент должен также каким-то образом зависеть от третьего и т.д. Это приводит к тому, что периодическая зависимость может существенно измениться после удаления автокорреляций первого порядка, т.е. после взятия разности с лагом 1).



Частные автокорреляции.
Частные автокорреляции.

Другой полезный метод исследования периодичности состоит в исследовании частной автокорреляционной функции (ЧАКФ), представляющей собой углубление понятия обычной автокорреляционной функции. В ЧАКФ устраняется зависимость между промежуточными наблюдениями (наблюдениями внутри лага). Другими словами, частная автокорреляция на данном лаге аналогична обычной автокорреляции, за исключением того, что при вычислении из нее удаляется влияние автокорреляций с меньшими лагами (см. Бокс и Дженкинс, 1976; см. также McDowall, McCleary, Meidinger, and Hay, 1980). На лаге 1 (когда нет промежуточных элементов внутри лага), частная автокорреляция равна, очевидно, обычной автокорреляции. На самом деле, частная автокорреляция дает более "чистую" картину периодических зависимостей.

Удаление периодической зависимости.
Удаление периодической зависимости.

Как отмечалось выше, периодическая составляющая для данного лага k может быть удалена взятием разности соответствующего порядка. Это означает, что из каждого i-го элемента ряда вычитается (i-k)-й элемент. Имеются два довода в пользу таких преобразований.

Во-первых, таким образом можно определить скрытые периодические составляющие ряда. Напомним, что автокорреляции на последовательных лагах зависимы. Поэтому удаление некоторых автокорреляций изменит другие автокорреляции, которые, возможно, подавляли их, и сделает некоторые другие сезонные составляющие более заметными.

Во-вторых, удаление сезонных составляющих делает ряд стационарным, что необходимо для применения АРПСС и других методов, например, спектрального анализа.

В начало

АРПСС Общее введение Два основных процесса Модель АРПСС Идентификация Оценивание параметров Оценивание модели Дополнительная информация о методах Анализа временных рядов дана также в следующих разделах: Идентификация модели временных рядов Прерванные временные ряды Экспоненциальное сглаживание Сезонная декомпозиция (метод Census I) Сезонная корректировка X-11 (метод Census II) Таблицы результатов корректировки X-11 Анализ распределенных лагов Одномерный анализ Фурье Кросс-спектральный анализ Основные понятия и принципы Быстрое преобразование Фурье  


Общее введение
Общее введение

Процедуры оценки параметров и прогнозирования, описанные в разделе Идентификация модели временных рядов, предполагают, что математическая модель процесса известна. В реальных данных часто нет отчетливо выраженных регулярных составляющих. Отдельные наблюдения содержат значительную ошибку, тогда как вы хотите не только выделить регулярные компоненты, но также построить прогноз. Методология АРПСС, разработанная Боксом и Дженкинсом (1976), позволяет это сделать. Данный метод чрезвычайно популярен во многих приложениях, и практика подтвердила его мощность и гибкость (Hoff, 1983; Pankratz, 1983; Vandaele, 1983). Однако из-за мощности и гибкости, АРПСС - сложный метод. Его не так просто использовать, и требуется большая практика, чтобы овладеть им. Хотя часто он дает удовлетворительные результаты, они зависят от квалификации пользователя (Bails and Peppers, 1982). Следующие разделы познакомят вас с его основными идеями. Для интересующихся кратким, рассчитанным на применение, (нематематическим) введением в АРПСС, рекомендуем книгу McCleary, Meidinger, and Hay (1980).




Два основных процесса
Два основных процесса

Процесс авторегрессии.
Процесс авторегрессии.

Большинство временных рядов содержат элементы, которые последовательно зависят друг от друга. Такую зависимость можно выразить следующим уравнением:

xt = + 1*x(t-1) + 2*x(t-2) + 3*x(t-3) + ... +



Здесь:
                - константа (свободный член),
 1, 2, 3   - параметры авторегрессии.

Вы видите, что каждое наблюдение есть сумма случайной компоненты (случайное воздействие, ) и линейной комбинации предыдущих наблюдений.

Требование стационарности.
Требование стационарности.

Заметим, что процесс авторегрессии будет стационарным только, если его параметры лежат в определенном диапазоне. Например, если имеется только один параметр, то он должен находиться в интервале -1<<+1. В противном случае, предыдущие значения будут накапливаться и значения последующих xt могут быть неограниченными, следовательно, ряд не будет стационарным. Если имеется несколько параметров авторегрессии, то можно определить аналогичные условия, обеспечивающие стационарность (см. например, Бокс и Дженкинс, 1976; Montgomery, 1990).

Процесс скользящего среднего.
Процесс скользящего среднего.

В отличие от процесса авторегрессии, в процессе скользящего среднего каждый элемент ряда подвержен суммарному воздействию предыдущих ошибок. В общем виде это можно записать следующим образом:

xt = µ + t - 1*(t-1) - 2*(t-2) - 3*(t-3) - ...

Здесь:
µ                - константа,
 1, 2, 3  - параметры скользящего среднего.

Другими словами, текущее наблюдение ряда представляет собой сумму случайной компоненты   (случайное воздействие, ) в данный момент и линейной комбинации случайных воздействий в предыдущие моменты времени.

Обратимость.
Обратимость.

Не вдаваясь в детали, отметим, что существует "двойственность" между процессами скользящего среднего и авторегрессии (см. например, Бокс и Дженкинс, 1976; Montgomery, Johnson, and Gardiner, 1990). Это означает, что приведенное выше уравнение скользящего среднего можно переписать (обратить) в виде уравнения авторегрессии (неограниченного порядка), и наоборот. Это так называемое свойство обратимости.


Имеются условия, аналогичные приведенным выше условиям стационарности, обеспечивающие обратимость модели.

  Модель АРПСС
Модель АРПСС

Модель авторегрессии и скользящего среднего.
Модель авторегрессии и скользящего среднего.

Общая модель, предложенная Боксом и Дженкинсом (1976) включает как параметры авторегрессии, так и параметры скользящего среднего. Именно, имеется три типа параметров модели: параметры авторегрессии (p), порядок разности (d), параметры скользящего среднего (q). В обозначениях Бокса и Дженкинса модель записывается как АРПСС (p, d, q). Например, модель (0, 1, 2) содержит 0 (нуль) параметров авторегрессии (p) и 2 параметра скользящего среднего (q), которые вычисляются для ряда после взятия разности с лагом 1.

Идентификация.
Идентификация.

Как отмечено ранее, для модели АРПСС необходимо, чтобы ряд был стационарным, это означает, что его среднее постоянно, а выборочные дисперсия и автокорреляция не меняются во времени. Поэтому обычно необходимо брать разности ряда до тех пор, пока он не станет стационарным (часто также применяют логарифмическое преобразование для стабилизации дисперсии). Число разностей, которые были взяты, чтобы достичь стационарности, определяются параметром d (см. предыдущий раздел). Для того чтобы определить необходимый порядок разности, нужно исследовать график ряда и автокоррелограмму. Сильные изменения уровня (сильные скачки вверх или вниз) обычно требуют взятия несезонной разности первого порядка (лаг=1). Сильные изменения наклона требуют взятия разности второго порядка. Сезонная составляющая требует взятия соответствующей сезонной разности (см. ниже). Если имеется медленное убывание выборочных коэффициентов автокорреляции в зависимости от лага, обычно берут разность первого порядка. Однако следует помнить, что для некоторых временных рядов нужно брать разности небольшого порядка или вовсе не брать их. Заметим, что чрезмерное количество взятых разностей приводит к менее стабильным оценкам коэффициентов.



На этом этапе ( который обычно называют идентификацией порядка модели, см. ниже) вы также должны решить, как много параметров авторегрессии (p) и скользящего среднего (q) должно присутствовать в эффективной и экономной модели процесса. (Экономность модели означает, что в ней имеется наименьшее число параметров и наибольшее число степеней свободы среди всех моделей, которые подгоняются к данным). На практике очень редко бывает, что число параметров p или q больше 2 (см. ниже более полное обсуждение).

Оценивание и прогноз.
Оценивание и прогноз.

Следующий, после идентификации, шаг (Оценивание) состоит в оценивании параметров модели (для чего используются процедуры минимизации функции потерь, см. ниже; более подробная информация о процедурах минимизации дана в разделе Нелинейное оценивание). Полученные оценки параметров используются на последнем этапе (Прогноз) для того, чтобы вычислить новые значения ряда и построить доверительный интервал для прогноза. Процесс оценивания проводится по преобразованным данным (подвергнутым применению разностного оператора). До построения прогноза нужно выполнить обратную операцию (интегрировать данные). Таким образом, прогноз методологии будет сравниваться с соответствующими исходными данными. На интегрирование данных указывает буква П в общем названии модели (АРПСС = Авторегрессионное Проинтегрированное Скользящее Среднее).

Константа в моделях АРПСС.
Константа в моделях АРПСС.

Дополнительно модели АРПСС могут содержать константу, интерпретация которой зависит от подгоняемой модели. Именно, если (1) в модели нет параметров авторегрессии, то константа есть среднее значение ряда, если (2) параметры авторегрессии имеются, то константа представляет собой свободный член. Если бралась разность ряда, то константа представляет собой среднее или свободный член преобразованного ряда. Например, если бралась первая разность (разность первого порядка), а параметров авторегрессии в модели нет, то константа представляет собой среднее значение преобразованного ряда и, следовательно, коэффициент наклона линейного тренда исходного.



Идентификация
Идентификация

Число оцениваемых параметров.
Число оцениваемых параметров.

Конечно, до того, как начать оценивание, вам необходимо решить, какой тип модели будет подбираться к данным, и какое количество параметров присутствует в модели, иными словами, нужно идентифицировать модель АРПСС. Основными инструментами идентификации порядка модели являются графики, автокорреляционная функция (АКФ), частная автокорреляционная функция (ЧАКФ). Это решение не является простым и требуется основательно поэкспериментировать с альтернативными моделями. Тем не менее, большинство встречающихся на практике временных рядов можно с достаточной степенью точности аппроксимировать одной из 5 основных моделей (см. ниже), которые можно идентифицировать по виду автокорреляционной (АКФ) и частной автокорреляционной функции (ЧАКФ). Ниже дается список этих моделей, основанный на рекомендациях Pankratz (1983); дополнительные практические советы даны в Hoff (1983), McCleary and Hay (1980), McDowall, McCleary, Meidinger, and Hay (1980), and Vandaele (1983). Отметим, что число параметров каждого вида невелико (меньше 2), поэтому нетрудно проверить альтернативные модели. Один параметр (p): АКФ - экспоненциально убывает; ЧАКФ - имеет резко выделяющееся значение для лага 1, нет корреляций на других лагах. Два параметра авторегрессии (p): АКФ имеет форму синусоиды или экспоненциально убывает; ЧАКФ имеет резко выделяющиеся значения на лагах 1, 2, нет корреляций на других лагах. Один параметр скользящего среднего (q): АКФ имеет резко выделяющееся значение на лаге 1, нет корреляций на других лагах. ЧАКФ экспоненциально убывает. Два параметра скользящего среднего (q): АКФ имеет резко выделяющиеся значения на лагах 1, 2, нет корреляций на других лагах. ЧАКФ имеет форму синусоиды или экспоненциально убывает. Один параметр авторегрессии (p) и один параметр скользящего среднего (q): АКФ экспоненциально убывает с лага 1; ЧАКФ - экспоненциально убывает с лага 1. Сезонные модели. Мультипликативная сезонная АРПСС представляет естественное развитие и обобщение обычной модели АРПСС на ряды, в которых имеется периодическая сезонная компонента.


В дополнении к несезонным параметрам, в модель вводятся сезонные параметры для определенного лага (устанавливаемого на этапе идентификации порядка модели). Аналогично параметрам простой модели АРПСС, эти параметры называются: сезонная авторегрессия (ps), сезонная разность (ds) и сезонное скользящее среднее (qs). Таким образом, полная сезонная АРПСС может быть записана как АРПСС (p,d,q)(ps,ds,qs). Например, модель (0,1,2)(0,1,1) включает 0 регулярных параметров авторегрессии, 2 регулярных параметра скользящего среднего и 1 параметр сезонного скользящего среднего. Эти параметры вычисляются для рядов, получаемых после взятия одной разности с лагом 1 и далее сезонной разности. Сезонный лаг, используемый для сезонных параметров, определяется на этапе идентификации порядка модели.

Общие рекомендации относительно выбора обычных параметров (с помощью АКФ и ЧАКФ) полностью применимы к сезонным моделям. Основное отличие состоит в том, что в сезонных рядах АКФ и ЧАКФ имеют существенные значения на лагах, кратных сезонному лагу (в дополнении к характерному поведению этих функций, описывающих регулярную (несезонную) компоненту АРПСС).

Оценивание параметров
Оценивание параметров

Существуют различные методы оценивания параметров, которые дают очень похожие оценки, но для данной модели одни оценки могут быть более эффективны, а другие менее эффективны. В общем, во время оценивания порядка модели используется так называемый квазиньютоновский алгоритм максимизации правдоподобия (вероятности) наблюдения значений ряда по значениям параметров (см. Нелинейное оценивание). Практически это требует вычисления (условных) сумм квадратов (SS) остатков модели. Имеются различные способы вычисления суммы квадратов остатков SS; вы можете выбрать: (1) приближенный метод максимального правдоподобия МакЛеода и Сейлза (1983), (2) приближенный метод максимального правдоподобия с итерациями назад, (3)точный метод максимального правдоподобия по Meларду (1984).

Сравнение методов.


Сравнение методов.

В общем, все методы дают очень похожие результаты. Также все методы показали примерно одинаковую эффективность на реальных данных. Однако метод 1 (см. выше) - самый быстрый, и им можно пользоваться для исследования очень длинных рядов (например, содержащих более 30,000 наблюдений). Метод Меларда (номер 3) может оказаться неэффективным, если оцениваются параметры сезонной модели с большим сезонным лагом (например, 365 дней). С другой стороны, вы можете использовать вначале приближенный метод максимального правдоподобия (для того, чтобы найти прикидочные оценки параметров), а затем точный метод; обычно требуется только несколько итераций точного метода (номер 3, выше), чтобы получить окончательные оценки.

Стандартные ошибки оценок.
Стандартные ошибки оценок.

Для всех оценок параметров вычисляются так называемые асимптотические стандартные ошибки, для вычисления которых используется матрица частных производных второго порядка, аппроксимируемая конечными разностями (см. также раздел Нелинейное оценивание).

Штраф.
Штраф.

Процедура оценивания минимизирует (условную) сумму квадратов остатков модели. Если модель не является адекватной, может случиться так, что оценки параметров на каком-то шаге станут неприемлемыми - очень большими (например, не удовлетворяют условию стационарности). В таком случае, SS будет приписано очень большое значение (штрафное значение). Обычно это "заставляет" итерационный процесс удалить параметры из недопустимой области. Однако в некоторых случаях и эта стратегия может оказаться неудачной, и вы все равно увидите на экране (во время процедуры оценивания) очень большие значения SS на серии итераций. В таких случаях следует с осторожностью оценивать пригодность модели. Если модель содержит много параметров и, возможно, имеется интервенция (см. ниже), то следует несколько раз испытать процесс оценивания с различными начальными. Если модель содержит много параметров и, возможно, интервенцию (см. ниже), вам следует повторить процедуру с различными начальными значениями параметров.



Оценивание модели
Оценивание модели

Оценки параметров.
Оценки параметров.

Если значения вычисляемой t статистики не значимы, соответствующие параметры в большинстве случаев удаляются из модели без ущерба подгонки.

Другой критерий качества.
Другой критерий качества.

Другой обычной мерой надежности модели является сравнение прогноза, построенного по урезанному ряду с "известными (исходными) данными".



Однако качественная модель должна не только давать достаточно точный прогноз, но быть экономной и иметь независимые остатки, содержащие только шум без систематических компонент (в частности, АКФ остатков не должна иметь какой-либо периодичности). Поэтому необходим всесторонний анализ остатков. Хорошей проверкой модели являются: (a) график остатков и изучение их трендов, (b) проверка АКФ остатков (на графике АКФ обычно отчетливо видна периодичность).

Анализ остатков.
Анализ остатков.

Если остатки систематически распределены (например, отрицательны в первой части ряда и примерно равны нуля во второй) или включают некоторую периодическую компоненту, то это свидетельствует о неадекватности модели. Анализ остатков чрезвычайно важен и необходим при анализе временных рядов. Процедура оценивания предполагает, что остатки не коррелированы и нормально распределены.

Ограничения.
Ограничения.

Следует напомнить, что модель АРПСС является подходящей только для рядов, которые являются стационарными (среднее, дисперсия и автокорреляция примерно постоянны во времени); для нестационарных рядов следует брать разности. Рекомендуется иметь, как минимум, 50 наблюдений в файле исходных данных. Также предполагается, что параметры модели постоянны, т.е. не меняются во времени.

Прерванные временные ряды

Обычный вопрос, возникающий при анализе временных рядов, состоит в следующем, воздействует или нет внешнее событие на последовательность наблюдений. Например, привела ли новая экономическая политика к росту экономики, как обещалось; изменил ли новый закон интенсивность преступлений и т.д.


В общем, нужно оценивать воздействия одного или нескольких дискретных событий на значения ряда. Этот вид анализа прерванных временных рядов подробно описан в книге McDowall, McCleary, Meidinger, and Hay (1980). Различают следующие три типа воздействий: (1) устойчивое скачкообразное, (2) устойчивое постепенное, (3) скачкообразное временное. См. также следующие разделы: Идентификация модели временных рядов АРПСС Экспоненциальное сглаживание Сезонная декомпозиция (метод Census I) Сезонная корректировка X-11 (метод Census II) Таблицы результатов корректировки X-11 Анализ распределенных лагов Одномерный анализ Фурье Кросс-спектральный анализ Основные понятия и принципы Быстрое преобразование Фурье

В начало

 


Экспоненциальное сглаживание Общее введение Простое экспоненциальное сглаживание Выбор лучшего значения параметра a (альфа) Индексы качества подгонки Сезонная и несезонная модели с трендом или без тренда См. также: Идентификация модели временных рядов АРПСС (Бокс и Дженкинс) и автокорреляции Прерванные временные ряды Сезонная декомпозиция (метод Census I) Сезонная корректировка X-11 (метод Census II) Таблицы результатов корректировки X-11 Анализ распределенных лагов Одномерный анализ Фурье Кросс-спектральный анализ Основные понятия и принципы Быстрое преобразование Фурье   Общее введение
Общее введение

Экспоненциальное сглаживание - это очень популярный метод прогнозирования многих временных рядов. Исторически метод был независимо открыт Броуном и Холтом. Броун служил на флоте США во время второй мировой войны, где занимался обнаружением подводных лодок и системами наведения. Позже он применил открытый им метод для прогнозирования спроса на запасные части. Свои идеи он описал в книге, вышедшей в свет в 1959 году. Исследования Холта были поддержаны Департаментом военно-морского флота США. Независимо друг от друга, Броун и Холт открыли экспоненциальное сглаживание для процессов с постоянным трендом, с линейным трендом и для рядов с сезонной составляющей.



Gardner (1985), предложил "единую" классификацию методов экспоненциального сглаживания. Превосходное введение в эти методы можно найти в книгах Makridakis, Wheelwright, and McGee (1983), Makridakis and Wheelwright (1989), Montgomery, Johnson, and Gardiner (1990).

Простое экспоненциальное сглаживание
Простое экспоненциальное сглаживание

Простая и прагматически ясная модель временного ряда имеет следующий вид: Xt = b + t, где b - константа и (эпсилон) - случайная ошибка. Константа b относительно стабильна на каждом временном интервале, но может также медленно изменяться со временем. Один из интуитивно ясных способов выделения b состоит в том, чтобы использовать сглаживание скользящим средним, в котором последним наблюдениям приписываются большие веса, чем предпоследним, предпоследним большие веса, чем пред-предпоследним и т.д. Простое экспоненциальное именно так и устроено. Здесь более старым наблюдениям приписываются экспоненциально убывающие веса, при этом, в отличие от скользящего среднего, учитываются все предшествующие наблюдения ряда, а не те, что попали в определенное окно. Точная формула простого экспоненциального сглаживания имеет следующий вид:

St = *Xt + (1-)*St-1

Когда эта формула применяется рекурсивно, то каждое новое сглаженное значение (которое является также прогнозом) вычисляется как взвешенное среднее текущего наблюдения и сглаженного ряда. Очевидно, результат сглаживания зависит от параметра (альфа). Если равно 1, то предыдущие наблюдения полностью игнорируются. Если равно 0, то игнорируются текущие наблюдения. Значения между 0, 1 дают промежуточные результаты.

Эмпирические исследования Makridakis и др. (1982; Makridakis, 1983) показали, что весьма часто простое экспоненциальное сглаживание дает достаточно точный прогноз.

  Выбор лучшего значения параметра (альфа)
Выбор лучшего значения параметра (альфа)

Gardner (1985) обсуждает различные теоретические и эмпирические аргументы в пользу выбора определенного параметра сглаживания.


Очевидно, из формулы, приведенной выше, следует, что должно попадать в интервал между 0 (нулем) и 1 (хотя Brenner et al., 1968, для дальнейшего применения анализа АРПСС считают, что 0<<2). Gardner (1985) сообщает, что на практике обычно рекомендуется брать меньше .30. Однако в исследовании Makridakis et al., (1982), большее .30, часто дает лучший прогноз. После обзора литературы, Gardner (1985) приходит к выводу, что лучше оценивать оптимально по данным (см. ниже), чем просто "гадать" или использовать искусственные рекомендации.

Оценивание лучшего значения с помощью данных.
Оценивание лучшего значения с помощью данных.

На практике параметр сглаживания часто ищется с поиском на сетке. Возможные значения параметра разбиваются сеткой с определенным шагом. Например, рассматривается сетка значений от = 0.1 до = 0.9, с шагом 0.1. Затем выбирается , для которого сумма квадратов (или средних квадратов) остатков (наблюдаемые значения минус прогнозы на шаг вперед) является минимальной.

Индексы качества подгонки
Индексы качества подгонки

Самый прямой способ оценки прогноза, полученного на основе определенного значения - построить график наблюдаемых значений и прогнозов на один шаг вперед. Этот график включает в себя также остатки (отложенные на правой оси Y). Из графика ясно видно, на каких участках прогноз лучше или хуже.



Такая визуальная проверка точности прогноза часто дает наилучшие результаты. Имеются также другие меры ошибки, которые можно использовать для определения оптимального параметра (см. Makridakis, Wheelwright, and McGee, 1983):

Средняя ошибка.
Средняя ошибка.

Средняя ошибка (СО) вычисляется простым усреднением ошибок на каждом шаге. Очевидным недостатком этой меры является то, что положительные и отрицательные ошибки аннулируют друг друга, поэтому она не является хорошим индикатором качества прогноза.

Средняя абсолютная ошибка.
Средняя абсолютная ошибка.

Средняя абсолютная ошибка (САО) вычисляется как среднее абсолютных ошибок.


Если она равна 0 (нулю), то имеем совершенную подгонку (прогноз). В сравнении со средней квадратической ошибкой, эта мера "не придает слишком большого значения" выбросам.

Сумма квадратов ошибок (SSE), среднеквадратическая ошибка.
Сумма квадратов ошибок (SSE), среднеквадратическая ошибка.

Эти величины вычисляются как сумма (или среднее) квадратов ошибок. Это наиболее часто используемые индексы качества подгонки.

Относительная ошибка (ОО).
Относительная ошибка (ОО).

Во всех предыдущих мерах использовались действительные значения ошибок. Представляется естественным выразить индексы качества подгонки в терминах относительных ошибок. Например, при прогнозе месячных продаж, которые могут сильно флуктуировать (например, по сезонам) из месяца в месяц, вы можете быть вполне удовлетворены прогнозом, если он имеет точность ?10%. Иными словами, при прогнозировании абсолютная ошибка может быть не так интересна как относительная. Чтобы учесть относительную ошибку, было предложено несколько различных индексов (см. Makridakis, Wheelwright, and McGee, 1983). В первом относительная ошибка вычисляется как:

ООt = 100*(Xt - Ft )/Xt

где Xt - наблюдаемое значение в момент времени t, и Ft - прогноз (сглаженное значение).

Средняя относительная ошибка (СОО).
Средняя относительная ошибка (СОО).

Это значение вычисляется как среднее относительных ошибок.

Средняя абсолютная относительная ошибка (САОО).
Средняя абсолютная относительная ошибка (САОО).

Как и в случае с обычной средней ошибкой отрицательные и положительные относительные ошибки будут подавлять друг друга. Поэтому для оценки качества подгонки в целом (для всего ряда) лучше использовать среднюю абсолютную относительную ошибку. Часто эта мера более выразительная, чем среднеквадратическая ошибка. Например, знание того, что точность прогноза ±5%, полезно само по себе, в то время как значение 30.8 для средней квадратической ошибки не может быть так просто проинтерпретировано.

Автоматический поиск лучшего параметра.
Автоматический поиск лучшего параметра.



Для минимизации средней квадратической ошибки, средней абсолютной ошибки или средней абсолютной относительной ошибки используется квази-ньютоновская процедура (та же, что и в АРПСС). В большинстве случаев эта процедура более эффективна, чем обычный перебор на сетке (особенно, если параметров сглаживания несколько), и оптимальное значение можно быстро найти.

Первое сглаженное значение
Первое сглаженное значение

S0. Если вы взгляните снова на формулу простого экспоненциального сглаживания, то увидите, что следует иметь значение S0 для вычисления первого сглаженного значения (прогноза). В зависимости от выбора параметра (в частности, если близко к 0), начальное значение сглаженного процесса может оказать существенное воздействие на прогноз для многих последующих наблюдений. Как и в других рекомендациях по применению экспоненциального сглаживания, рекомендуется брать начальное значение, дающее наилучший прогноз. С другой стороны, влияние выбора уменьшается с длиной ряда и становится некритичным при большом числе наблюдений.

Сезонная и несезонная модели с трендом или без тренда
Сезонная и несезонная модели с трендом или без тренда

В дополнение к простому экспоненциальному сглаживанию, были предложены более сложные модели, включающие сезонную компоненту и трендом. Общая идея таких моделей состоит в том, что прогнозы вычисляются не только по предыдущим наблюдениям (как в простом экспоненциальном сглаживании), но и с некоторыми задержками, что позволяет независимо оценить тренд и сезонную составляющую. Gardner (1985) обсудил различные модели в терминах сезонности (отсутствует, аддитивная сезонность, мультипликативная) и тренда (отсутствует, линейный тренд, экспоненциальный, демпфированный).

Аддитивная и мультипликативная сезонность.
Аддитивная и мультипликативная сезонность.

Многие временные ряды имеют сезонные компоненты. Например, продажи игрушек имеют пики в ноябре, декабре и, возможно, летом, когда дети находятся на отдыхе. Эта периодичность имеет место каждый год.


Однако относительный размер продаж может слегка изменяться из года в год. Таким образом, имеет смысл независимо экспоненциально сгладить сезонную компоненту с дополнительным параметром, обычно обозначаемым как (дельта). Сезонные компоненты, по природе своей, могут быть аддитивными или мультипликативными. Например, в течение декабря продажи определенного вида игрушек увеличиваются на 1 миллион долларов каждый год. Для того чтобы учесть сезонное колебание, вы можете добавить в прогноз на каждый декабрь 1 миллион долларов (сверх соответствующего годового среднего). В этом случае сезонность - аддитивная. Альтернативно, пусть в декабре продажи увеличились на 40%, т.е. в 1.4 раза. Тогда, если общие продажи малы, то абсолютное (в долларах) увеличение продаж в декабре тоже относительно мало (процент роста константа). Если в целом продажи большие, то абсолютное (в долларах) увеличение продаж будет пропорционально больше. Снова, в этом случае продажи увеличатся в определенное число раз, и сезонность будет мультипликативной (в данном случае мультипликативная сезонная составляющая была бы равна 1.4). На графике различие между двумя видами сезонности состоит в том, что в аддитивной модели сезонные флуктуации не зависят от значений ряда, тогда как в мультипликативной модели величина сезонных флуктуаций зависит от значений временного ряда.

Параметр сезонного сглаживания .
Параметр сезонного сглаживания .

В общем, прогноз на один шаг вперед вычисляется следующим образом (для моделей без тренда; для моделей с линейным и экспоненциальным трендом, тренд добавляется; см. ниже):

Аддитивная модель:

Прогнозt = St + It-p

Мультипликативная модель:

Прогнозt = St*It-p

В этой формуле St обозначает (простое) экспоненциально сглаженное значение ряда в момент t, и It-p обозначает сглаженный сезонный фактор в момент t минус p (p - длина сезона). Таким образом, в сравнении с простым экспоненциальным сглаживанием, прогноз "улучшается" добавлением или умножением сезонной компоненты.


Эта компонента оценивается независимо с помощью простого экспоненциального сглаживания следующим образом:

Аддитивная модель:

It = It-p + *(1-)*et

Мультипликативная модель:

It = It-p + *(1-)*et/St

Обратите внимание, что предсказанная сезонная компонента в момент t вычисляется, как соответствующая компонента на последнем сезонном цикле плюс ошибка (et, наблюдаемое минус прогнозируемое значение в момент t). Ясно, что параметр принимает значения между 0 и 1. Если он равен нулю, то сезонная составляющая на следующем цикле та же, что и на предыдущем. Если равен 1, то сезонная составляющая "максимально" меняется на каждом шаге из-за соответствующей ошибки (множитель (1-) не рассматривается из-за краткости введения). В большинстве случаев, когда сезонность присутствует, оптимальное значение лежит между 0 и 1.

Линейный, экспоненциальный, демпфированный тренд.
Линейный, экспоненциальный, демпфированный тренд.

Возвращаясь к примеру с игрушками, мы можем увидеть наличие линейного тренда (например, каждый год продажи увеличивались на 1 миллион), экспоненциального (например, каждый год продажи возрастают в 1.3 раза) или демпфированного тренда (в первом году продажи возросли на 1 миллион долларов; во втором увеличение составило только 80% по сравнению с предыдущим, т.е. на $800,000; в следующем году вновь увеличение было только на 80%, т.е. на $800,000 * .8 = $640,000 и т.д.). Каждый тип тренда по-своему проявляется в данных. В целом изменение тренда - медленное в течение времени, и опять (как и сезонную компоненту) имеет смысл экспоненциально сгладить его с отдельным параметром [обозначаемым (гамма) - для линейного и экспоненциального тренда, (фи) - для демпфированного тренда].

Параметры сглаживания (линейный и экспоненциальный тренд) и (демпфированный тренд).
Параметры сглаживания (линейный и экспоненциальный тренд) и (демпфированный тренд).

Аналогично сезонной компоненте компонента тренда включается в процесс экспоненциального сглаживания. Сглаживание ее производится в каждый момент времени независимо от других компонент с соответствующими параметрами.


Если равно 0, то тренд постоянен для всех значений временного ряда (и для всех прогнозов). Если равно 1, то тренд "максимально" определяется ошибками наблюдений. Параметр учитывает, как сильно изменяется тренд, т.е. как быстро он "демпфируется" или, наоборот, возрастает.

В начало

 


Сезонная декомпозиция (метод Census I) Общее введение Вычисления См. также: Идентификация модели временных рядов АРПСС (Бокс и Дженкинс) и автокорреляции Прерванные временные ряды Экспоненциальное сглаживание Сезонная корректировка X-11 (метод Census II) Таблицы результатов корректировки X-11 Анализ распределенных лагов Одномерный анализ Фурье Кросс-спектральный анализ Основные понятия и принципы Быстрое преобразование Фурье  


Общее введение
Общее введение

Предположим, что у вас имеются ежемесячные данные о пассажиропотоке на международных авиалиниях за 12 лет (см. Бокс и Дженкинс, 1976). Если изобразить эти данные на графике, то будет хорошо видно, что (1) объем пассажиропотока имеет во времени возрастающий линейный тренд, и (2) в ряде имеется ежегодно повторяющаяся закономерность - сезонность (большинство перевозок приходится на летние месяцы, кроме того, имеется пик меньшей высоты в районе декабрьских каникул). Цель сезонной декомпозиции и корректировки как раз и состоит в том, чтобы отделить эти компоненты, то есть разложить ряд на составляющую тренда, сезонную компоненту и оставшуюся нерегулярную составляющую. "Классический" прием, позволяющий выполнить такую декомпозицию, известен как метод Census I. Этот метод описывается и обсуждается в работах Makridakis, Wheelwright, and McGee (1983) и Makridakis and Wheelwright (1989).

Общая модель.
Общая модель.

Основная идея сезонной декомпозиции проста. В общем случае временной ряд типа того, который описан выше, можно представить себе состоящим из четырех различных компонент: (1) сезонной компоненты (обозначается St, где t обозначает момент времени), (2) тренда (Tt), (3) циклической компоненты (Ct) и (4) случайной, нерегулярной компоненты или флуктуации (It).


Разница между циклической и сезонной компонентой состоит в том, что последняя имеет регулярную (сезонную) периодичность, тогда как циклические факторы обычно имеют более длительный эффект, который к тому же меняется от цикла к циклу. В методе Census I тренд и циклическую компоненту обычно объединяют в одну тренд-циклическую компоненту (TCt). Конкретные функциональные взаимосвязи между этими компонентами могут иметь самый разный вид. Однако, можно выделить два основных способа, с помощью которых они могут взаимодействовать: аддитивно и мультипликативно:

Аддитивная модель:

Xt = TCt + St + It

Мультипликативная модель:

Xt = Tt*Ct*St*It

Здесь Xt обозначает значение временного ряда в момент времени t. Если имеются какие-то априорные сведения о циклических факторах, влияющих на ряд (например, циклы деловой конъюнктуры), то можно использовать оценки для различных компонент для составления прогноза будущих значений ряда. (Однако для прогнозирования предпочтительнее экспоненциальное сглаживание, позволяющее учитывать сезонную составляющую и тренд.)

Аддитивная и мультипликативная сезонность.
Аддитивная и мультипликативная сезонность.

Рассмотрим на примере различие между аддитивной и мультипликативной сезонными компонентами. График объема продаж детских игрушек, вероятно, будет иметь ежегодный пик в ноябре-декабре, и другой - существенно меньший по высоте - в летние месяцы, приходящийся на каникулы. Такая сезонная закономерность будет повторяться каждый год. По своей природе сезонная компонента может быть аддитивной или мультипликативной. Так, например, каждый год объем продаж некоторой конкретной игрушки может увеличиваться в декабре на 3 миллиона долларов. Поэтому вы можете учесть эти сезонные изменения, прибавляя к своему прогнозу на декабрь 3 миллиона. Здесь мы имеем аддитивную сезонность. Может получиться иначе. В декабре объем продаж некоторой игрушки может увеличиваться на 40%, то есть умножаться на множитель 1.4. Это значит, например, что если средний объем продаж этой игрушки невелик, то абсолютное (в денежном выражении) увеличение этого объема в декабре также будет относительно небольшим (но в процентном исчислении оно будет постоянным); если же игрушка продается хорошо, то и абсолютный (в долларах) рост объема продаж будет значительным.


Здесь опять, объем продаж возрастает в число раз, равное определенному множителю, а сезонная компонента, по своей природе, мультипликативная компонента (в данном случае равная 1.4). Если перейти к графикам временных рядов, то различие между этими двумя видами сезонности будет проявляться так: в аддитивном случае ряд будет иметь постоянные сезонные колебания, величина которых не зависит от общего уровня значений ряда; в мультипликативном случае величина сезонных колебаний будет меняться в зависимости от общего уровня значений ряда.

Аддитивный и мультипликативный тренд-цикл.
Аддитивный и мультипликативный тренд-цикл.

Рассмотренный пример можно расширить, чтобы проиллюстрировать понятия аддитивной и мультипликативной тренд-циклических компонент. В случае с игрушками, тренд "моды" может привести к устойчивому росту продаж (например, это может быть общий тренд в сторону игрушек образовательной направленности). Как и сезонная компонента, этот тренд может быть по своей природе аддитивным (продажи ежегодно увеличиваются на 3 миллиона долларов) или мультипликативным (продажи ежегодно увеличиваются на 30%, или возрастают в 1.3 раза). Кроме того, объем продаж может содержать циклические компоненты. Повторим еще раз, что циклическая компонента отличается от сезонной тем, что она обычно имеет большую временную протяженность и проявляется через неравные промежутки времени. Так, например, некоторая игрушка может быть особенно "горячей" в течение летнего сезона (например, кукла, изображающая персонаж популярного мультфильма, которая к тому же агрессивно рекламируется). Как и в предыдущих случаях, такая циклическая компонента может изменять объем продаж аддитивно, либо мультипликативно.

Вычисления
Вычисления

В вычислительном отношении процедура метода Сезонной декомпозиции (Census I) следует стандартным формулам, см. Makridakis, Wheelwright, and McGee (1983) или Makridakis and Wheelwright (1989).



Скользящее среднее.
Скользящее среднее.

Сначала вычисляется скользящее среднее для временного ряда, при этом ширина окна берется равной периоду сезонности.


Если период сезонности - четное число, пользователь может выбрать одну из двух возможностей: брать скользящее среднее с одинаковыми весами или же с неравными весами так, что первое и последнее наблюдения в окне имеют усредненные веса.

Отношения или разности.
Отношения или разности.

После взятия скользящих средних вся сезонная (т.е. внутри сезона) изменчивость будет исключена, и поэтому разность (в случае аддитивной модели) или отношение (для мультипликативной модели) между наблюдаемым и сглаженным рядом будет выделять сезонную составляющую (плюс нерегулярную компоненту). Более точно, ряд скользящих средних вычитается из наблюдаемого ряда (в аддитивной модели) или же значения наблюдаемого ряда делятся на значения скользящих средних (в мультипликативной модели).

Сезонная составляющая.
Сезонная составляющая.

На следующем шаге вычисляется сезонная составляющая, как среднее (для аддитивных моделей) или урезанное среднее (для мультипликативных моделей) всех значений ряда, соответствующих данной точке сезонного интервала.



Сезонная корректировка ряда.
Сезонная корректировка ряда.

Исходный ряд можно скорректировать, вычитая из него (аддитивная модель) или деля его значения на (мультипликативная модель) значения сезонной составляющей.



Получающийся в результате ряд называется сезонной корректировкой ряда (из ряда убрана сезонная составляющая)..

Тренд-циклическая компонента.
Тренд-циклическая компонента.

Напомним, что циклическая компонента отличается от сезонной компоненты тем, что продолжительность цикла, как правило, больше, чем один сезонный период, и разные циклы могут иметь разную продолжительность. Приближение для объединенной тренд-циклической компоненты можно получить, применяя к ряду с сезонной поправкой процедуру 5-точечного (центрированного) взвешенного скользящего среднего с весами 1, 2, 3, 2, 1.

Случайная или нерегулярная компонента.
Случайная или нерегулярная компонента.

На последнем шаге выделяется случайная или нерегулярная компонента (погрешность) путем вычитания из ряда с сезонной поправкой (аддитивная модель) или делением этого ряда (мультипликативная модель) на тренд-циклическую компоненту.

В начало

Сезонная корректировка X-11 (метод Census II)

Общие идеи, лежащие в основе сезонной декомпозиции и корректировки, изложены в разделе, посвященном методу сезонной корректировки Census I (см. Сезонная декомпозиция (метод Census I)). Метод Census II (2) является развитием и уточнением обычного метода корректировки. На протяжении многих лет различные варианты метода Census II развивались в Бюро Переписи США (US Census Bureau); один из вариантов этого метода, получивший широкую известность и наиболее часто применяемый в государственных органах и сфере бизнеса, называется "вариант X-11 метода Census II" (см. Shiskin, Young, and Musgrave, 1967). Впоследствии этот усовершенствованный вариант метода Census II стал называться просто X-11. Помимо документации, которую можно получить из Census Bureau, подробное описание метода дано в работах Makridakis, Wheelwright and McGee (1983), Makridakis and Wheelwright (1989).

За дополнительной информацией обратитесь к следующим разделам: Сезонная корректировка: основные идеи и термины Метод Census II Таблицы результатов корректировки X-11 Подробное описание всех таблиц результатов, вычисляемых в методе X-11 За дальнейшей информацией обратитесь к Анализу временных рядов и следующим разделам: Идентификация модели временных рядов АРПСС (Бокс и Дженкинс) и автокорреляции Прерванные временные ряды Экспоненциальное сглаживание Сезонная декомпозиция (метод Census I) Анализ распределенных лагов Одномерный анализ Фурье Кросс-спектральный анализ Основные понятия и принципы Быстрое преобразование Фурье  


Сезонная корректировка: основные идеи и термины
Сезонная корректировка: основные идеи и термины

Предположим, что у вас имеются ежемесячные данные о пассажиропотоке на международных авиалиниях за 12 лет (см. Бокс и Дженкинс, 1976). Если изобразить эти данные на графике, то будет хорошо видно, что (1) объем пассажиропотока имеет во времени возрастающий линейный тренд, и что (2) в ряде имеется ежегодно повторяющаяся закономерность - сезонность (большинство перевозок приходится на летние месяцы, кроме того, имеется пик меньшей высоты в районе декабрьских каникул).


Цель сезонной декомпозиции и корректировки как раз и состоит в том, чтобы отделить эти компоненты, то есть разложить ряд на составляющую тренда, сезонную компоненту и оставшуюся нерегулярную составляющую. "Классический" прием, позволяющий выполнить такую декомпозицию, известен как метод Census I (см. раздел Census I). Этот метод описывается и обсуждается в работах Makridakis, Wheelwright, and McGee (1983) и Makridakis and Wheelwright (1989).

Общая модель.
Общая модель.

Основная идея сезонной декомпозиции проста. В общем случае временной ряд типа того, который описан выше, можно представить себе состоящим из четырех различных компонент: (1) сезонной компоненты (обозначается St, где t обозначает момент времени), (2) тренда (Tt), (3) циклической компоненты (Ct) и (4) случайной, нерегулярной компоненты или флуктуации (It). Разница между циклической и сезонной компонентой состоит в том, что последняя имеет регулярную (сезонную) периодичность, тогда как циклические факторы обычно имеют более длительный эффект, который к тому же меняется от цикла к циклу. В методе Census I тренд и циклическую компоненту обычно объединяют в одну тренд-циклическую компоненту (TCt). Конкретные функциональные взаимосвязи между этими компонентами могут иметь самый разный вид. Однако, можно выделить два основных способа, с помощью которых они могут взаимодействовать: аддитивно и мультипликативно:

Аддитивная модель:

Xt = TCt + St + It

Мультипликативная модель:

Xt = Tt*Ct*St*It

Здесь Xt обозначает значение временного ряда в момент времени t.

Если имеются какие-то априорные сведения о циклических факторах, влияющих на ряд (например, циклы деловой конъюнктуры), то можно использовать оценки для различных компонент для составления прогноза будущих значений ряда. (Однако для прогнозирования предпочтительнее экспоненциальное сглаживание, позволяющее учитывать сезонную составляющую и тренд.)

Аддитивная и мультипликативная сезонность.
Аддитивная и мультипликативная сезонность.



Рассмотрим на примере различие между аддитивной и мультипликативной сезонными компонентами. График объема продаж детских игрушек, вероятно, будет иметь ежегодный пик в ноябре-декабре, и другой - существенно меньший по высоте - в летние месяцы, приходящийся на каникулы. Такая сезонная закономерность будет повторяться каждый год. По своей природе сезонная компонента может быть аддитивной или мультипликативной. Так, например, каждый год объем продаж некоторой конкретной игрушки может увеличиваться в декабре на 3 миллиона долларов. Поэтому вы можете учесть эти сезонные изменения, прибавляя к своему прогнозу на декабрь 3 миллиона. Здесь мы имеем аддитивную сезонность. Может получиться иначе. В декабре объем продаж некоторой игрушки может увеличиваться на 40%, то есть умножаться на множитель 1.4. Это значит, например, что если средний объем продаж этой игрушки невелик, то абсолютное (в денежном выражении) увеличение этого объема в декабре также будет относительно небольшим (но в процентном исчислении оно будет постоянным); если же игрушка продается хорошо, то и абсолютный (в долларах) рост объема продаж будет значительным. Здесь опять, объем продаж возрастает в число раз, равное определенному множителю, а сезонная компонента, по своей природе, мультипликативная компонента (в данном случае равная 1.4). Если перейти к графикам временных рядов, то различие между этими двумя видами сезонности будет проявляться так: в аддитивном случае ряд будет иметь постоянные сезонные колебания, величина которых не зависит от общего уровня значений ряда; в мультипликативном случае величина сезонных колебаний будет меняться в зависимости от общего уровня значений ряда.

Аддитивный и мультипликативный тренд-цикл.
Аддитивный и мультипликативный тренд-цикл.

Рассмотренный пример можно расширить, чтобы проиллюстрировать понятия аддитивной и мультипликативной тренд-циклических компонент. В случае с игрушками, тренд "моды" может привести к устойчивому росту продаж (например, это может быть общий тренд в сторону игрушек образовательной направленности).


Как и сезонная компонента, этот тренд может быть по своей природе аддитивным (продажи ежегодно увеличиваются на 3 миллиона долларов) или мультипликативным (продажи ежегодно увеличиваются на 30%, или возрастают в 1.3 раза). Кроме того, объем продаж может содержать циклические компоненты. Повторим еще раз, что циклическая компонента отличается от сезонной тем, что она обычно имеет большую временную протяженность и проявляется через неравные промежутки времени. Так, например, некоторая игрушка может быть особенно "горячей" в течение летнего сезона (например, кукла, изображающая персонаж популярного мультфильма, которая к тому же агрессивно рекламируется). Как и в предыдущих случаях, такая циклическая компонента может изменять объем продаж аддитивно, либо мультипликативно.

Метод Census II
Метод Census II

Основной метод сезонной декомпозиции и корректировки, рассмотренный в разделе Сезонная корректировка: основные идеи и термины, может быть усовершенствован различными способами. На самом деле, в отличие от многих методов моделирования временных рядов (в частности, АРПСС), которые основаны на определенной теоретической модели, вариант X-11 метода Census II представляет собой просто результат многочисленных специально разработанных приемов и усовершенствований, которые доказали свою работоспособность в многолетней практике решения реальных задач (см. Burman, 1979, Kendall and Ord, 1990, Makridakis and Wheelwright, 1989; Wallis, 1974). Некоторые из наиболее важных усовершенствований перечислены ниже.

Поправка на число рабочих дней.
Поправка на число рабочих дней.

В месяцах разное число дней и разное число рабочих дней. Если мы анализируем, например, цифры ежемесячной выручки парка аттракционов, то разница в числе суббот и воскресений (пиковые дни) в разных месяцах существенным образом скажется на различиях в ежемесячных показателях дохода. Вариант X-11 метода Census II дает пользователю возможность проверить, присутствует ли во временном ряду этот эффект числа рабочих дней, и если да, то внести соответствующие поправки.



Выбросы.
Выбросы.

Большинство реальных временных рядов содержит выбросы, то есть резко выделяющиеся наблюдения, вызванные какими-то исключительными событиями. Например, забастовка персонала может сильно повлиять на месячные или годовые показатели выпуска продукции фирмы. Такие выбросы могут исказить оценки сезонной компоненты и тренда. В процедуре X-11 предусмотрены корректировки на случай появления выбросов, основанные на использовании "принципов статистического контроля": значения, выходящие за определенный диапазон (который определяется в терминах, кратных сигма, т.е. стандартных отклонений), могут быть преобразованы или вовсе пропущены, и только после этого будут вычисляться окончательные оценки параметров сезонности.

Последовательные уточнения.
Последовательные уточнения.

Корректировки, связанные с наличием выбросов и различным числом рабочих дней можно производить многократно, чтобы последовательно получать для компонент оценки все лучшего качества. В методе X-11 делается несколько последовательных уточнений оценок для получения окончательных компонент тренд-цикличности и сезонности, нерегулярной составляющей, и самого временного ряда с сезонными поправками.

Критерии и итоговые статистики.
Критерии и итоговые статистики.

Помимо оценки основных компонент ряда, можно вычислить различные сводные статистики. Например, можно сформировать таблицы дисперсионного анализа для проверки значимости фактора сезонной изменчивости и ряда и фактора рабочих дней (см. выше), процедура метода X-11 вычисляет также ежемесячные относительные изменения в случайной и тренд-циклической компонентах. С увеличением продолжительности временного промежутка, измеряемого в месяцах или, в случае квартального варианта метода X-11 - в кварталах года, изменения в тренд-циклической компоненте, вообще говоря, будут нарастать, в то время как изменения случайной составляющей должны оставаться примерно на одном уровне. Средняя длина временного интервала, на котором изменения тренд-циклической компоненты становятся примерно равными изменениям случайной компоненты, называется месяцем (кварталом) циклического доминирования, или сокращенно МЦД (соответственно КЦД).


Например, если МЦД равно двум, то на сроках более двух месяцев тренд-циклическая компонента станет доминировать над флуктуациями нерегулярной (случайной) компоненты. Эти и другие результаты более подробно будут обсуждаться далее.

Таблицы результатов корректировки X-11
Таблицы результатов корректировки X-11

Вычисления, которые производятся в процедуре   X-11, лучше всего обсуждать в контексте таблиц результатов, которые при этом выдаются. Процедура корректировки разбивается на семь этапов, которые обычно обозначаются буквами A - G. Априорная корректировка (помесячная сезонная корректировка). Перед тем, как к временному ряду, содержащему ежемесячные значения, будет применяться какая-либо сезонная корректировка, могут быть произведены различные корректировки, заданные пользователем. Можно ввести еще один временной ряд, содержащий априорные корректирующие факторы; значения этого ряда будут вычитаться из исходного ряда (аддитивная модель), или же значения исходного ряда будут поделены на значения корректирующего ряда (мультипликативная модель). В случае мультипликативной модели пользователь может также определить свои собственные поправочные коэффициенты (веса) на число рабочих дней. Эти веса будут использоваться для корректировки ежемесячных наблюдений, так чтобы учитывалось число рабочих дней в этом месяце. Предварительное оценивание вариации числа рабочих дней (месячный вариант X-11) и весов. На следующем шаге вычисляются предварительные поправочные коэффициенты на число рабочих дней (только в месячном варианте X-11) и веса, позволяющие уменьшить эффект выбросов. Окончательное оценивание вариации числа рабочих дней и нерегулярных весов (месячный вариант X-11). Поправки и веса, вычисленные в пункте B, используются для построения улучшенных оценок тренд-циклической и сезонной компонент. Эти улучшенные оценки используются для окончательного вычисления факторов числа рабочих дней (в месячном варианте X-11) и весов. Окончательное оценивание сезонных факторов, тренд-циклической, нерегулярной и сезонно скорректированной компонент ряда. Окончательные значения факторов рабочих дней и весов, вычисленные в пункте C, используются для вычисления окончательных оценок для компонент ряда. Модифицированные ряды: исходный, сезонно скорректированный и нерегулярный. Исходный и окончательный сезонно скорректированный ряды, а также нерегулярная компонента модифицируются путем сглаживания выбросов.


Полученные в результате этого, модифицированные ряды позволяют пользователю проверить устойчивость сезонной корректировки. Месяц (квартал) циклического доминирования (МЦД, КЦД), скользящее среднее и сводные показатели. IНа этом этапе вычислений рассчитываются различные сводные характеристики (см. далее), позволяющие пользователю исследовать относительную важность разных компонент, среднюю флуктуацию от месяца к месяцу (от квартала к кварталу), среднее число идущих подряд изменений в одну сторону и др. Графики. Наконец, вы можете построить различные графики итоговых результатов. Например, можно построить окончательно скорректированный ряд в хронологическом порядке или по месяцам (см. ниже).  


Подробное описание всех таблиц результатов, вычисляемых в методе X-11
Подробное описание всех таблиц результатов, вычисляемых в методе X-11

На каждом из этапов A - G (см. раздел Таблицы результатов корректировки X-11) вычислялись различные таблицы результатов. Обычно все они нумеруются, а также им приписывается буква, соответствующая этапу анализа. Например, таблица B 11 содержит предварительно сезонно скорректированный ряд; C 11 - это более точно сезонно скорректированный ряд, а D 11 - окончательный сезонно скорректированный ряд. Далее приводится перечень всех таблиц. Таблицы, помеченные звездочкой (*), недоступны (или неприменимы) при анализе квартальных показателей. Кроме того, в случае квартальной корректировки некоторые из описанных ниже вычислений несколько видоизменяются. Так, например, для вычисления сезонных факторов вместо 12-периодного (т.е. 12-месячного) скользящего среднего используется 4-периодное (4-квартальное) скользящее среднее; предварительная тренд-циклическая компонента вычисляется по центрированному 4-периодному скользящему среднему, а окончательная оценка тренд-циклической компоненты вычисляется по 5-точечному среднему Хендерсона.

В соответствии со стандартом метода X-11, принятым Бюро переписи США, предусмотрены три степени подробности вывода: Стандартный (17 - 27 таблиц), Длинный (27 - 39 таблиц) и Полный (44 - 59 таблиц).


Имеется также возможность выводить только таблицы результатов, выбранные пользователем. В следующих далее описаниях таблиц, буквы С, Д и П рядом с названием таблицы указывают, какие таблицы выводятся и/или распечатываются в соответствующем варианте вывода. (Для графиков предусмотрены два уровня подробности вывода: Стандартный и Все.)

Щелкните на имени таблицы для получения информации о ней.

* A 1. Исходный ряд (С)

* A 2. Априорные месячные поправки (С)

* A 3. Исходный ряд, скорректированный с помощью априорных месячных поправок (С)

* A 4. Априорные поправки на рабочие дни (С)

B 1. Ряд после априорной корректировки либо исходный ряд (С)

B 2. Тренд-цикл (Д)

B 3. Немодифицированные S-I разности или отношения (П)

B 4. Значения для замены выбросов S-I разностей (отношений) (П)

B 5. Сезонная составляющая (П)

B 6. Сезонная корректировка ряда (П)

B 7. Тренд-цикл (Д)

B 8. Немодифицированные S-I разности (отношения) (П)

B 9. Значения для замены выбросов S-I разностей (отношений) (П)

B 10. Сезонная составляющая (Д)

B 11. Сезонная корректировка ряда (П)

B 12. (не используется)

B 13. Нерегулярная составляющая ряда (Д)

Таблицы B 14 - B 16, B 18 и B 19: Поправка на число рабочих дней. Эти таблицы доступны только при анализе ежемесячных данных. Число разных дней недели (понедельников, вторников и т.д.) колеблется от месяца к месяцу. Бывают ряды, в которых различия в числе рабочих дней в месяце могут давать заметный разброс ежемесячных показателей (например, месячный доход парка аттракционов сильно зависит от того, сколько в этом месяце было выходных дней). Пользователь имеет возможность определить начальные веса для каждого дня недели (см. A 4), и/или эти веса могут быть оценены по данным (пользователь также может сделать использование этих весов условным, т.е. только в тех случаях, когда они объясняют значительную часть дисперсии).

* B 14. Выбросы нерегулярной составляющей, исключенные из регрессии рабочих дней (Д)

* B 15. Предварительная регрессия рабочих дней (Д)

* B 16. Поправки на число рабочих дней, полученные из коэффициентов регрессии (П)

B 17. Предварительные веса нерегулярной компоненты (Д)

* B 18. Поправки на число рабочих дней, полученные из комбинированных весов дней недели (П)

* B 19. Исходный ряд с поправками на рабочие дни и априорную вариацию (П)

C 1. Исходный ряд, модифицированный с помощью предварительных весов, с поправкой на рабочие дни и априорную вариацию (Д)

C 2. Тренд-цикл (П)

C 3. (не используется)

C 4. Модифицированные S-I разности (отношения) (П)

C 5. Сезонная составляющая (П)

C 6. Сезонная корректировка ряда (П)

C 7. Тренд-цикл (Д)

C 8. (не используется)

C 9. Модифицированные S-I разности (отношения) (П)

C 10. Сезонная составляющая (Д)

C 11. Сезонная корректировка ряда (П)

C 12. (не используется)

C 13. Нерегулярная составляющая (С)

Таблицы C 14 - C 16, C 18 и C 19: Поправка на число рабочих дней. Эти таблицы доступны только при анализе ежемесячных данных и если при этом требуется поправка на различное число рабочих дней. В этом случае поправки на число рабочих дней вычисляются по уточненным значениям сезонно скорректированных рядов аналогично тому, как это делалось в пункте B (B 14 - B 16, B 18, B 19).

* C 14. Выбросы нерегулярной составляющей, исключенные из регрессии рабочих дней (С)

* C 15. Регрессия рабочих дней - окончательный вариант (С)

* C 16. Поправки на число рабочих дней, полученные из коэффициентов регрессии, - окончательный вариант (С)

C 17. Окончательные веса нерегулярной компоненты (С)

* C 18. Поправки на число рабочих дней, полученные из комбинированных весов дней недели - окончательный вариант (С)

* C 19. Исходный ряд с поправками на рабочие дни и априорную вариацию (С)

D 1. Исходный ряд, модифицированный с помощью окончательных весов, с поправкой на рабочие дни и априорную вариацию (Д)

D 2. Тренд-цикл (П)

D 3. (не используется)

D 4. Модифицированные S-I разности (отношения) (П)

D 5. Сезонная составляющая (П)

D 6. Сезонная корректировка ряда (П)

D 7. Тренд-цикл (Д)

D 8. Немодифицированные S-I разности (отношения) - окончательный вариант (С)

D 9. Окончательные значения для замены выбросов S-I разностей (отношений) (С)

D 10. Сезонная составляющая - окончательный вариант (С)

D 11. Сезонная корректировка ряда - окончательный вариант (С)

D 12. Тренд-циклическая компонента - окончательный вариант (С)

D 13. Нерегулярная составляющая - окончательный вариант (С)

E 1. Модифицированный исходный ряд (С)

E 2. Модифицированный ряд с сезонной поправкой (С)

E 3. Модифицированная нерегулярная составляющая (С)

E 4. Разности (отношения) годовых сумм (С)

E 5. Разности (относительные изменения) исходного ряда (С)

E 6. Разности (относительные изменения) окончательного варианта ряда с сезонной поправкой (С)

F 1. МЦД (КЦД) скользящее среднее (С)

F 2. Сводные показатели (С)

G 1. График (С)

G 2. График (С)

G 3. График (В)

G 4. График (В)

В начало

Анализ распределенных лагов Общая цель Общая модель Распределенный лаг Алмона За дальнейшей информацией обратитесь к Анализу временных рядов и следующим разделам: Идентификация модели временных рядов АРПСС (Бокс и Дженкинс) и автокорреляции Вводный обзор АРПСС Прерванные временные ряды Экспоненциальное сглаживание Сезонная декомпозиция (метод Census I) Сезонная корректировка X-11 (метод Census II) Таблицы результатов корректировки X-11 Одномерный анализ Фурье Кросс-спектральный анализ Основные понятия и принципы Быстрое преобразование Фурье  


Общая цель
Общая цель

Анализ распределенных лагов - это специальный метод оценки запаздывающей зависимости между рядами. Например, предположим, вы производите компьютерные программы и хотите установить зависимость между числом запросов, поступивших от покупателей, и числом реальных заказов. Вы могли бы записывать эти данные ежемесячно в течение года и затем рассмотреть зависимость между двумя переменными: число запросов и число заказов зависит от запросов, но зависит с запаздыванием. Однако очевидно, что запросы предшествуют заказам, поэтому можно ожидать, что число заказов. Иными словами, в зависимости между числом запросов и числом продаж имеется временной сдвиг (лаг) (см. также автокорреляции и кросскорреляции).

Такого рода зависимости с запаздыванием особенно часто возникают в эконометрике. Например, доход от инвестиций в новое оборудование отчетливо проявится не сразу, а только через определенное время. Более высокий доход изменяет выбор жилья людьми; однако эта зависимость, очевидно, тоже проявляется с запаздыванием. [Подобные задачи возникают в страховании, где временной ряд клиентов и ряд денежных поступлений сдвинуты друг относительно друга].

Во всех этих случаях, имеется независимая или объясняющая переменная, которая воздействует на зависимые переменные с некоторым запаздыванием (лагом). Метод распределенных лагов позволяет исследовать такого рода зависимость.

Подробные обсуждения зависимостей с распределенными лагами имеются в эконометрических учебниках, например, в Judge, Griffith, Hill, Luetkepohl, and Lee (1985), Maddala (1977), and Fomby, Hill, and Johnson (1984).


Ниже дается краткое описание этих методов. Предполагается, что вы знакомы с понятием корреляции (см. Основные статистики и таблицы), кросскорреляции и основными идеями множественной регрессии (см. Множественная регрессия).




Общая модель
Общая модель

Пусть y - зависимая переменная, a независимая или объясняющая x. Эти переменные измеряются несколько раз в течение определенного отрезка времени. В некоторых учебниках по эконометрике зависимая переменная называется также эндогенной переменной, a зависимая или объясняемая переменная экзогенной переменной. Простейший способ описать зависимость между этими двумя переменными дает следующее линейное уравнение:

Yt = i*xt-i

В этом уравнении значение зависимой переменной в момент времени t является линейной функцией переменной x, измеренной в моменты t, t-1, t-2 и т.д. Таким образом, зависимая переменная представляет собой линейные функции x и x, сдвинутых на 1, 2, и т.д. временные периоды. Бета коэффициенты (i) могут рассматриваться как параметры наклона в этом уравнении. Будем рассматривать это уравнение как специальный случай уравнения линейной регрессии (см. раздел Множественная регрессия). Если коэффициент переменной с определенным запаздыванием (лагом) значим, то можно заключить, что переменная y предсказывается (или объясняется) с запаздыванием.

 


Распределенный лаг Алмона
Распределенный лаг Алмона

Обычная проблема, возникающая в множественной регрессии, состоит в том, что соседние значения x сильно коррелируют. В самом крайнем случае, это приводит к тому, что корреляционная матрица не будет обратимой и коэффициенты бета не могут быть вычислены. В менее экстремальных ситуациях вычисления этих коэффициентов и их стандартные ошибки становятся ненадежными из-за вычислительных ошибок (ошибок округления). В контексте множественной регрессии эта проблема хорошо известна как проблема мультиколлинеарности (см. раздел Множественная регрессия).

Алмон (1965) предложил специальную процедуру, которая в данном случае уменьшает мультиколлинеарность.


Именно, пусть каждый неизвестный коэффициент записан в виде:

i = 0 + 1*i + ... + q*iq

Алмон показал, что во многих случаях (в частности, чтобы избежать мультиколлинеарности) легче оценить коэффициенты альфа, чем непосредственно коэффициенты бета. Такой метод оценивания коэффициентов бета называется полиномиальной аппроксимацией.

Неправильная спецификация.
Неправильная спецификация.

Общая проблема полиномиальной аппроксимации, состоит в том, что длина лага и степень полинома неизвестны заранее. Последствия неправильного определения (спецификации) этих параметров потенциально серьезны (в силу смещения, возникающего в оценках при неправильном задании параметров). Этот вопрос подробно обсуждается в книгах Frost (1975), Schmidt and Waud (1973), Schmidt and Sickles (1975) и Trivedi and Pagan (1979).




Одномерный анализ Фурье

В спектральном анализе исследуются периодические модели данных. Цель анализа - разложить комплексные временные ряды с циклическими компонентами на несколько основных синусоидальных функций с определенной длиной волн. Термин "спектральный" - своеобразная метафора для описания природы этого анализа. Предположим, вы изучаете луч белого солнечного света, который, на первый взгляд, кажется хаотически составленным из света с различными длинами волн. Однако, пропуская его через призму, вы можете отделить волны разной длины или периодов, которые составляют белый свет. Фактически, применяя этот метод, вы можете теперь распознавать и различать разные источники света. Таким образом, распознавая существенные основные периодические компоненты, вы узнали что-то об интересующем вас явлении. В сущности, применение спектрального анализа к временным рядам подобно пропусканию света через призму. В результате успешного анализа можно обнаружить всего несколько повторяющихся циклов различной длины в интересующих вас временных рядах, которые, на первый взгляд, выглядят как случайный шум.

Наиболее известный пример применения спектрального анализа - циклическая природа солнечных пятен (например, см.


Блумфилд, 1976 или Шамвэй, 1988). Оказывается, что активность солнечных пятен имеет 11-ти летний цикл. Другие примеры небесных явлений, изменения погоды, колебания в товарных ценах, экономическая активность и т.д. также часто используются в литературе для демонстрации этого метода. В отличие от АРПСС или метода экспоненциального сглаживания (см. разделы АРПСС и Экспоненциальное сглаживание), цель спектрального анализа - распознать сезонные колебания различной длины, в то время как в предшествующих типах анализа, длина сезонных компонент обычно известна (или предполагается) заранее и затем включается в некоторые теоретические модели скользящего среднего или автокорреляции.

Классический текст по спектральному анализу - Bloomfield (1976); однако другие подробные обсуждения могут быть найдены в Jenkins and Watts (1968), Brillinger (1975), Brigham (1974), Elliott and Rao (1982), Priestley (1981), Shumway (1988) или Wei (1989).

За дальнейшей информацией обратитесь к Анализу временных рядов и следующим разделам: Основные понятия и принципы Быстрое преобразование Фурье Идентификация модели временных рядов АРПСС (Бокс и Дженкинс) и автокорреляции Вводный обзор АРПСС Прерванные временные ряды Анализ распределенных лагов Сезонная декомпозиция (метод Census I) Экспоненциальное сглаживание Кросс-спектральный анализ  


Кросс-спектральный анализ Общее введение Основные понятия и принципы Результаты для каждой переменной Кросс-периодограмма, кросс-плотность, квадратурная плотность и кросс-амплитуда Квадрат когерентности, усиление и фазовый сдвиг Как создавались данные для примера За дальнейшей информацией обратитесь к Анализу временных рядов и следующим разделам: Идентификация модели временных рядов АРПСС (Бокс и Дженкинс) и автокорреляции Вводный обзор АРПСС Прерванные временные ряды Экспоненциальное сглаживание Сезонная декомпозиция (метод Census I) Сезонная корректировка X-11 (метод Census II) Таблицы результатов корректировки X-11 Анализ распределенных лагов Одномерный анализ Фурье Основные понятия и принципы Быстрое преобразование Фурье




Общее введение
Общее введение

Кросс- спектральный анализ развивает Одномерный анализ Фурье и позволяет анализировать одновременно два ряда. Мы предполагаем, что вы уже прочитали введение к разделу одномерного спектрального анализа. Подробное обсуждение кросс-спектрального анализа можно найти в книгах Bloomfield (1976), Jenkins and Watts (1968), Brillinger (1975), Brigham (1974), Elliott and Rao (1982), Priestley (1981), Shumway (1988), or Wei (1989).

Периодичность ряда на определенных частотах.
Периодичность ряда на определенных частотах.

Наиболее известный пример применения спектрального анализа - циклическая природа солнечных пятен (например, см. Блумфилд, 1976 или Шамвэй, 1988). Оказывается, что активность солнечных пятен имеет 11-ти летний цикл. Другие примеры небесных явлений, изменения погоды, колебания в товарных ценах, экономическая активность и т.д. также часто используются в литературе для демонстрации этого метода.

Основные понятия и принципы
Основные понятия и принципы

Простой пример.
Простой пример.

Рассмотрим следующие два ряда с 16 наблюдениями:

ПЕРЕМ1 ПЕРЕМ2 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

1.000 1.637 1.148 -.058 -.713 -.383 .006 -.483 -1.441 -1.637 -.707 .331 .441 -.058 -.006 .924	-.058 -.713 -.383 .006 -.483 -1.441 -1.637 -.707 .331 .441 -.058 -.006 .924 1.713 1.365 .266

С первого взгляда нелегко рассмотреть взаимосвязь между двумя рядами. Тем не менее, как показано ниже, ряды создавались так, что содержат две сильно коррелируемые периодичности. Далее показаны части таблицы результатов из кросс-спектрального анализа (спектральные оценки были сглажены окном Парзена ширины 3).

Незавмсимая (X): ПЕРЕМ1
Зависимая (Y): ПЕРЕМ2  
Частота  
Период X
плотность Y
плотность Кросс
плотность Кросс
квадр. Кросс
амплит.

0.000000 .062500 .125000 .187500 .250000 .312500 .375000 .437500 .500000	16.00000 8.00000 5.33333 4.00000 3.20000 2.66667 2.28571 2.00000	.000000 8.094709 .058771 3.617294 .333005 .091897 .052575 .040248 .037115	.024292 7.798284 .100936 3.845154 .278685 .067630 .036056 .026633 0.000000	-.00000 2.35583 -.04755 -2.92645 -.26941 -.07435 -.04253 -.03256 0.00000	0.00000 -7.58781 .06059 2.31191 .14221 .02622 .00930 .00342 0.00000	.000000 7.945114 .077020 3.729484 .304637 .078835 .043539 .032740 0.000000

  Результаты для каждой переменной
Результаты для каждой переменной

Полная таблица результатов содержит все спектральные статистики, вычисленные для каждого ряда, как описано в разделе Одномерный анализ Фурье. Взглянув на приведенные выше результаты, очевидно, что оба ряда имеют основные периодичности на частотах .0625 и .1875.

  Кросс-периодограмма, кросс-плотность, квадратурная плотность и кросс-амплитуда
Кросс-периодограмма, кросс-плотность, квадратурная плотность и кросс-амплитуда

Аналогично результатам для одной переменной, полная итоговая таблица результатов также покажет значения периодограммы для кросс-периодограммы. Однако кросс-спектр состоит из комплексных чисел, которые могут быть разделены на действительную и мнимую части. Они могут быть сглажены для вычисления оценок кросс-плотности и квадратурной плотности (квадр-плотность для краткости), соответственно. (Причины сглаживания и различные функции весов для сглаживания обсуждаются в разделе Одномерный анализ Фурье.) Квадратный корень из суммы квадратов значений кросс-плотности и квадр-плотности называется кросс-амплитудой. Кросс-амплитуда может интерпретироваться как мера ковариации между соответствующими частотными компонентами двух рядов. Таким образом из результатов, показанных в таблице результатов выше, можно заключить, что частотные компоненты .0625 и .1875 двух рядов взаимосвязаны.

Квадрат когерентности, усиление и фазовый сдвиг
Квадрат когерентности, усиление и фазовый сдвиг

Существуют дополнительные статистики, которые будут показаны в полной итоговой таблице результатов.

Квадрат когерентности.
Квадрат когерентности.

Можно нормировать значения кросс-амплитуды, возведя их в квадрат и разделив на произведение оценок спектральной плотности каждого ряда. Результат называется квадратом когерентности, который может быть проинтерпретирован как квадрат коэффициента корреляции (см. раздел Корреляции); т.е. значение когерентности - это квадрат корреляции между циклическими компонентами двух рядов соответствующей частоты.


Однако значения когерентности не следует объяснять таким образом; например, когда оценки спектральной плотности обоих рядов очень малы, могут получиться большие значения когерентности (делитель в выражении когерентности может быть очень маленьким), даже если нет существенных циклических компонент в каждом ряду соответствующей частоты.

Усиление.
Усиление.

Значение усиления в анализе вычисляется делением значения кросс-амплитуды на оценки спектральной плотности одного или двух рядов. Следовательно, может быть вычислено два значения усиления, которые могут интерпретироваться как стандартные коэффициенты регрессии, соответствующей частоты, полученные методом наименьших квадратов.

Фазовый сдвиг.
Фазовый сдвиг.

В заключение, оценки фазового сдвига вычисляются как арктангенс (tan**-1) коэффициента пропорциональности оценки квадр-плотности и оценки кросс-плотности. Оценки фазового сдвига (обычно обозначаемые греческой буквой y) измеряют, насколько каждая частотная компонента одного ряда опережает частотные компоненты другого.

Как создавались данные для примера
Как создавались данные для примера

Теперь вернемся к примеру данных, приведенному выше. Большие оценки спектральной плотности для обоих рядов и значения кросс-амплитуды для частот = 0.0625 и = .1875 предполагают две существенных синхронных периодичности с этими частотами в обоих рядах. Фактически, два ряда создавались как:

v1 = cos(2**.0625*(v0-1)) + .75*sin(2**.2*(v0-1))

v2 = cos(2**.0625*(v0+2)) + .75*sin(2**.2*(v0+2))

(где v0 - номер наблюдения). Действительно, анализ, представленный в этом обзоре, очень хорошо воспроизводит периодичность, заложенную в данные.

 


Спектральный анализ - Основные понятия и принципы Частота и период Общая структура модели Простой пример Периодограмма Проблема рассеяния Добавление констант во временной ряд (пэддинг) Косинус-сглаживание Окна данных и оценки спектральной плотности Подготовка данных к анализу Результаты для случая, когда в ряде отсутствует периодичность За дальнейшей информацией обратитесь к Анализу временных рядов и следующим разделам: Идентификация модели временных рядов АРПСС (Бокс и Дженкинс) и автокорреляции Вводный обзор АРПСС Прерванные временные ряды Экспоненциальное сглаживание Сезонная декомпозиция (метод Census I) Сезонная корректировка X-11 (метод Census II) Таблицы результатов корректировки X-11 Анализ распределенных лагов Одномерный анализ Фурье Кросс-спектральный анализ Быстрое преобразование Фурье




Частота и период
Частота и период

Длина волны функций синуса или косинуса, как правило, выражается числом циклов (периодов) в единицу времени (Частота), часто обозначается греческой буквой ню (; в некоторых учебниках также используют f). Например, временной ряд, состоящий из количества писем, обрабатываемых почтой, может иметь 12 циклов в году. Первого числа каждого месяца отправляется большое количество корреспонденции (много счетов приходит именно первого числа каждого месяца); затем, к середине месяца, количество корреспонденции уменьшается; и затем вновь возрастает к концу месяца. Поэтому каждый месяц колебания в количестве корреспонденции, обрабатываемой почтовым отделением, будут проходить полный цикл. Таким образом, если единица анализа - один год, то будет равно 12 (поскольку имеется 12 циклов в году). Конечно, могут быть и другие циклы с различными частотами. Например, годичные циклы (=1) и, возможно, недельные циклы (=52 недели в год).

Период Т функций синуса или косинуса определяется как продолжительность по времени полного цикла. Таким образом, это обратная величина к частоте: T = 1/. Возвратимся к примеру с почтой из предыдущего абзаца, здесь месячный цикл будет равен 1/12 = 0.0833 года. Другими словами, это период составляет 0.0833 года.

Общая структура модели
Общая структура модели

Как было отмечено ранее, цель спектрального анализа - разложить ряд на функции синусов и косинусов различных частот, для определения тех, появление которых особенно существенно и значимо. Один из возможных способов сделать это - решить задачу линейной множественной регрессии (см. раздел Множественная регрессия), где зависимая переменная -наблюдаемый временной ряд, а независимые переменные или регрессоры: функции синусов всех возможных (дискретных) частот. Такая модель линейной множественной регрессии может быть записана как:

xt = a0 + [ak*cos(k*t) + bk*sin(k*t)]    (для k = 1 до q)

Следующее общее понятие классического гармонического анализа в этом уравнении - (лямбда) -это круговая частота, выраженная в радианах в единицу времени, т.е. = 2**k, где - константа пи = 3.1416 и k = k/q.


Здесь важно осознать, что вычислительная задача подгонки функций синусов и косинусов разных длин к данным может быть решена с помощью множественной линейной регрессии. Заметим, что коэффициенты ak при косинусах и коэффициенты bk при синусах - это коэффициенты регрессии, показывающие степень, с которой соответствующие функции коррелируют с данными [заметим, что сами синусы и косинусы на различных частотах не коррелированы или, другим языком, ортогональны. Таким образом, мы имеем дело с частным случаем разложения по ортогональным полиномам.] Всего существует q различных синусов и косинусов (см. также Множественная регрессия); интуитивно ясно, что число функций синусов и косинусов не может быть больше числа данных в ряде. Не вдаваясь в подробности, отметим, если n - количество данных, то будет n/2+1 функций косинусов и n/2-1 функций синусов. Другими словами, различных синусоидальных волн будет столько же, сколько данных, и вы сможете полностью воспроизвести ряд по основным функциям. (Заметим, если количество данных в ряде нечетно, то последнее наблюдение обычно опускается. Для определения синусоидальной функции нужно иметь, по крайней мере, две точки: высокого и низкого пика.)

В итоге, спектральный анализ определяет корреляцию функций синусов и косинусов различной частоты с наблюдаемыми данными. Если найденная корреляция (коэффициент при определенном синусе или косинусе) велика, то можно заключить, что существует строгая периодичность на соответствующей частоте в данных.

Комплексные числа (действительные и мнимые числа).
Комплексные числа (действительные и мнимые числа).

Во многих учебниках по спектральному анализу структурная модель, показанная выше, представлена в комплексных числах; т.е. параметры оцениваемого процесса описаны с помощью действительной и мнимой части преобразования Фурье. Комплексное число состоит из действительного и мнимого числа. Мнимые числа, по определению, - это числа, умноженные на константу i, где i определяется как квадратный корень из -1.


Очевидно, корень квадратный из -1 не существует в обычном сознании (отсюда термин мнимое число); однако арифметические операции над мнимыми числами могут производиться естественным образом [например, (i*2)**2= -4]. Полезно представление действительных и мнимых чисел, образующих двумерную координатную плоскость, где горизонтальная или X-ось представляет все действительные числа, а вертикальная или Y-ось представляет все мнимые числа. Комплексные числа могут быть представлены точками на двумерной плоскости. Например, комплексное число 3+i*2 может быть представлено точкой с координатами {3,2} на этой плоскости. Можно также представить комплексные числа как углы; например, можно соединить точку, соответствующую комплексному числу на плоскости с началом координат (комплексное число 0+i*0), и измерить угол наклона этого вектора к горизонтальной оси. Таким образом интуитивно ясно, каким образом формула спектрального разложения, показанная выше, может быть переписана в комплексной области. В таком виде математические вычисления часто более изящны и проще в выполнении, поэтому многие учебники предпочитают представление спектрального анализа в комплексных числах.

Простой пример
Простой пример

Шамвэй (1988) предлагает следующий простой пример для объяснения спектрального анализа. Создадим ряд из 16 наблюдений, полученных из уравнения, показанного ниже, а затем посмотрим, каким образом можно извлечь из него информацию. Сначала создадим переменную и определим ее как:

x = 1*cos(2**.0625*(v0-1)) + .75*sin(2**.2*(v0-1))

Эта переменная состоит из двух основных периодичностей - первая с частотой =.0625 (или периодом 1/=16; одно наблюдение составляет 1/16-ю длины полного цикла, или весь цикл содержит каждые 16 наблюдений) и вторая с частотой =.2 (или периодом 5). Коэффициент при косинусе (1.0) больше чем коэффициент при синусе (.75). Итоговая таблица результатов спектрального анализа показана ниже.

  Спектральный анализ: ПЕРЕМ1 (shumex.sta)
Число наблюдений: 16  
t Час-
тота  
Период Косинус
корэфф. Синус
корэфф. Периодо-
грамма

0 1 2 3 4 5 6 7 8	.0000 .0625 .1250 .1875 .2500 .3125 .3750 .4375 .5000	16.00 8.00 5.33 4.00 3.20 2.67 2.29 2.00	.000 1.006 .033 .374 -.144 -.089 -.075 -.070 -.068	0.000 .028 .079 .559 -.144 -.060 -.031 -.014 0.000	.000 8.095 .059 3.617 .333 .092 .053 .040 .037

Теперь рассмотрим столбцы таблицы результатов. Ясно, что наибольший коэффициент при косинусах расположен напротив частоты .0625. Наибольший коэффициент при синусах соответствует частоте .1875. Таким образом, эти две частоты, которые были "внесены" в данные, отчетливо проявились.

  Периодограмма
Периодограмма

Функции синусов и косинусов независимы (или ортогональны); поэтому можно просуммировать квадраты коэффициентов для каждой частоты, чтобы вычислить периодограмму. Более часто, значения периодограммы вычисляются как:

Pk = синус-коэффициентk2 + косинус-коэффициентk2 * N/2

где Pk - значения периодограммы на частоте k , и N - общая длина ряда. Значения периодограммы можно интерпретировать как дисперсию (вариацию) данных на соответствующей частоте. Обычно значения периодограммы изображаются в зависимости от частот или периодов.



  Проблема рассеяния
Проблема рассеяния

В примере, приведенном выше, функция синуса с частотой 0.2 была "вставлена" в ряд. Однако из-за того, что длина ряда равна 16, ни одна из частот, полученных в таблице результатов, не совпадает в точности с этой частотой. На практике в этих случаях часто оказывается, что соответствующая частота "рассеивается" на близкие частоты. Например, могут быть найдены большие значения периодограммы для двух близких частот, когда в действительности существует только одна основная функция синуса или косинуса с частотой, которая попадает на одну из этих частот или лежит между найденными частотами. Существует три подхода к решению проблемы рассеяния: При помощи добавление констант во временной ряда ряда можно увеличить частоты, Применяя сглаживание ряда перед анализом, можно уменьшить рассеяние или Применяя сглаживание периодограммы, можно идентифицировать основные частотные области или (спектральные плотности), которые существенно влияют на циклическое поведение ряда. Ниже смотрите описание каждого из этих подходов.

  Добавление констант во временной ряд (пэддинг)


Добавление констант во временной ряд (пэддинг)

Так как частотные величины вычисляются как N/t, можно просто добавить в ряд константы (например, нули), и таким образом получить увеличение частот. Фактически, если вы добавите в файл данных, описанный в примере выше, десять нулей, результаты не изменятся; т.е. наибольшие пики периодограммы будут находиться по-прежнему на частотах близких к .0625 и .2. (Добавление констант во временной ряд также часто желательно для увеличения вычислительной эффективности; см. ниже.)

Косинус-сглаживание
Косинус-сглаживание

Так называемый процесс косинус-сглаживания - рекомендуемое преобразование ряда, предшествующее спектральному анализу. Оно обычно приводит к уменьшению рассеяния в периодограмме. Логическое обоснование этого преобразования подробно объясняется в книге Bloomfield (1976, стр. 80-94). По существу, количественное отношение (p) данных в начале и в конце ряда преобразуется при помощи умножения на веса:

wt = 0.5*{1-cos[*(t - 0.5)/m]}     (для t=0 до m-1)
wt = 0.5*{1-cos[*(N - t + 0.5)/m]}     (для t=N-m до N-1)

где m выбирается так, чтобы 2*m/N было равно коэффициенту пропорциональности сглаживаемых данных (p).

  Окна данных и оценки спектральной плотности
Окна данных и оценки спектральной плотности

На практике, при анализе данных обычно не очень важно точно определить частоты основных функций синусов или косинусов. Скорее, т.к. значения периодограммы - объект существенного случайного колебания, можно столкнуться с проблемой многих хаотических пиков периодограммы. В этом случае хотелось бы найти частоты с большими спектральными плотностями, т.е. частотные области, состоящие из многих близких частот, которые вносят наибольший вклад в периодическое поведение всего ряда. Это может быть достигнуто путем сглаживания значений периодограммы с помощью преобразования взвешенного скользящего среднего. Предположим, ширина окна скользящего среднего равна m (должно быть нечетным числом); следующие наиболее часто используемые преобразования (заметим: p = (m-1)/2).



Окно Даниэля (равные веса).
Окно Даниэля (равные веса).

Окно Даниэля (Daniell, 1946) означает простое ( с равными весами) сглаживание скользящим средним значений периодограммы; т.е. каждая оценка спектральной плотности вычисляется как среднее m/2 предыдущих и последующих значений периодограммы.

Окно Тьюки.
Окно Тьюки.

В окне Тьюки (Blackman and Tukey, 1958) или Тьюки-Ханна (Hanning) (названное в честь Julius Von Hann), для каждой частоты веса для взвешенного скользящего среднего значений периодограммы вычисляются как:

wj = 0.5 + 0.5*cos(*j/p)(для j=0 до p)
w-j = wj    (для j 0)

Окно Хемминга.
Окно Хемминга.

В окне Хемминга (названного в честь R. W. Hamming) или Тьюки-Хемминга (Blackman and Tukey, 1958), для каждой частоты, веса для взвешенного скользящего среднего значений периодограммы вычисляются как:

wj = 0.54 + 0.46*cos(*j/p)    (для j=0 до p)
w-j = wj    (для j 0)

Окно Парзена.
Окно Парзена.

В окне Парзена (Parzen, 1961), для каждой частоты, веса для взвешенного скользящего среднего значений периодограммы вычисляются как:

wj = 1-6*(j/p)2 + 6*(j/p)3(для j = 0 до p/2)
wj = 2*(1-j/p)3    (для j = p/2 + 1 до p)
w-j = wj    (для j 0)

Окно Бартлетта.
Окно Бартлетта.

В окне Бартлетта (Bartlett, 1950) веса вычисляются как:

wj = 1-(j/p)    (для j = 0 до p)
w-j = wj    (для j 0)

За исключением окна Даниэля, все весовые функции приписывают больший вес сглаживаемому наблюдению, находящемуся в центре окна и меньшие веса значениям по мере удаления от центра. Во многих случаях, все эти окна данных получают очень похожие результаты.

  Подготовка данных к анализу
Подготовка данных к анализу

Теперь рассмотрим несколько других практических моментов спектрального анализа. Обычно, полезно вычесть среднее из значений ряда и удалить тренд (чтобы добиться стационарности) перед анализом. Иначе периодограмма и спектральная плотность "забьются" очень большим значением первого коэффициента при косинусе (с частотой 0.0).


По существу, среднее - это цикл частоты 0 (нуль) в единицу времени; т.е. константа. Аналогично, тренд также не представляет интереса, когда нужно выделить периодичность в ряде. Фактически оба этих эффекта могут заслонить более интересные периодичности в данных, поэтому и среднее, и (линейный) тренд следует удалить из ряда перед анализом. Иногда также полезно сгладить данные перед анализом, чтобы убрать случайный шум, который может засорять существенные периодические циклы в периодограмме.

Результаты для случая, когда в ряде отсутствует периодичность
Результаты для случая, когда в ряде отсутствует периодичность

В заключение, зададим вопрос: что, если повторяющихся циклов в данных нет, т.е. если каждое наблюдение совершенно независимо от всех других наблюдений? Если распределение наблюдений соответствует нормальному, такой временной ряд может быть белым шумом (подобный белый шум можно услышать, настраивая радио). Если исходный ряд - белый шум, то значения периодограммы будут иметь экспоненциальное распределение. Таким образом, проверкой на экспоненциальность значений периодограммы можно узнать, отличается ли исходный ряд от белого шума. Пользователь может также построить одновыборочную статистику d статистику Колмогорова-Смирнова (cм. также раздел Непараметрическая статистика и распределения).

Проверка, что шум - белый в ограниченной полосе частот.
Проверка, что шум - белый в ограниченной полосе частот.

Заметим, что также можно получить значения периодограммы для ограниченной частотной области. Снова, если введенный ряд - белый шум с соответствующими частотами (т.е. если нет существенных периодических циклов этих частот), то распределение значений периодограммы должно быть снова экспоненциальным.

В начало

Быстрое преобразование Фурье (БПФ) Общее введение Вычисление БПФ во временных рядах За дальнейшей информацией обратитесь к Анализу временных рядов и следующим разделам: Идентификация модели временных рядов АРПСС (Бокс и Дженкинс) и автокорреляции Вводный обзор АРПСС Прерванные временные ряды Экспоненциальное сглаживание Сезонная декомпозиция (метод Census I) Сезонная корректировка X-11 (метод Census II) Таблицы результатов корректировки X-11 Анализ распределенных лагов Одномерный анализ Фурье Кросс-спектральный анализ Основные понятия и принципы  




Общее введение
Общее введение

Интерпретация результатов спектрального анализа обсуждается в разделе Основные понятия и принципы, однако там мы не обсуждали вычислительные проблемы, которые в действительности очень важны. До середины 1960-х для представления спектрального разложения использовались точные формулы для нахождения параметров синусов и косинусов. Соответствующие вычисления требовали как минимум N**2 (комплексных) умножений. Таким образом, даже сегодня высокоскоростному компьютеру потребовалось бы очень много времени для анализа даже небольшого временного ряда (для 8,000 наблюдений потребовалось бы по меньшей мере 64 миллиона умножений).

Ситуация кардинально изменилась с открытием так называемого алгоритма быстрого преобразования Фурье, или БПФ для краткости. Достаточно сказать, что при применении алгоритма БПФ время выполнения спектрального анализа ряда длины N стало пропорционально N*log2(N) что конечно является огромным прогрессом.

Однако недостаток стандартного алгоритма БПФ состоит в том, что число данных ряда должно быть равным степени 2 (т.е. 16, 64, 128, 256, ...). Обычно это приводит к необходимости добавлять нули во временной ряд, который, как описано выше, в большинстве случаев не меняет характерные пики периодограммы или оценки спектральной плотности. Тем не менее, в некоторых случаях, когда единица времени значительна, добавление констант во временной ряд может сделать результаты более громоздкими.

Вычисление БПФ во временных рядах
Вычисление БПФ во временных рядах

Выполнение быстрого преобразования Фурье чрезвычайно эффективно. На большинстве стандартных компьютеров, ряд с более чем 100,000 наблюдений легко анализируется. Однако существует несколько моментов, которые надо помнить при анализе рядов большого размера.

Как упоминалось ранее, для применения стандартного (и наиболее эффективного) алгоритма БПФ требуется, чтобы длина исходного ряда была равна степени 2. Если это не так, должны быть проведены дополнительные вычисления.


Будут использоваться простые точные вычислительные формулы, пока исходный ряд относительно мал, и вычисления можно выполнить за относительно короткое время. Для длинных временных рядов, чтобы применить алгоритм БПФ, используется основной подход, описанный Monro и Branch (1976). Этот метод требует значительно больше памяти; однако ряд рассматриваемой длины может анализироваться все еще очень быстро, даже если число наблюдений не является степенью 2.

Для временных рядов, длина которых не равна степени 2, мы можем дать следующие рекомендации: если размер исходного ряда не превосходит средний размер (т.е. имеется только несколько тысяч наблюдений), не стоит беспокоиться. Анализ займет несколько секунд. Для анализа средних и больших рядов (например, содержащих свыше 100,000 наблюдений), добавьте в ряд константы (например нули) до тех пор, пока длина ряда не станет степенью 2 и затем примените косинус-сглаживание ряда в разведочной части анализа ваших данных.

Дополнительная информация по методам анализа данных, добычи данных, визуализации и прогнозированию содержится на Портале StatSoft (http://www.statsoft.ru/home/portal/default.asp) и в Углубленном Учебнике StatSoft (Учебник с формулами).


(c) Copyright StatSoft, Inc., 1984-2001
STATISTICA является торговой маркой StatSoft, Inc.

Анализ выживаемости

Анализ выживаемости

  Общие цели Цензурированные наблюдения Аналитические методы Анализ таблиц времен жизни Число изучаемых объектов Доля умерших Доля выживших Кумулятивная доля выживших (функция выживания) Плотность вероятности Функция интенсивности Медиана ожидаемого времени жизни Объем выборки Подгонка распределения Общее знакомство Оценивание Согласие Графики Множительные оценки Каплана-Мейера Сравнение выборок Общее знакомство Доступные критерии Выбор двухвыборочного критерия Критерий для нескольких выборок Неравные доли цензурированных наблюдений Регрессионные модели Общее знакомство Модель пропорциональных интенсивностей Кокса Модель пропорциональных интенсивностей Кокса с зависящими от времени ковариатами Экспоненциальная регрессия Нормальная и логнормальная регрессия Стратифицированный анализ

Общие цели Цензурированные наблюдения Аналитические методы Анализ таблиц времен жизни Число изучаемых объектов Доля умерших Доля выживших Кумулятивная доля выживших (функция выживания) Плотность вероятности Функция интенсивности Медиана ожидаемого времени жизни Объем выборки Подгонка распределения Общее знакомство Оценивание Согласие Графики Множительные оценки Каплана-Мейера Сравнение выборок Общее знакомство Доступные критерии Выбор двухвыборочного критерия Критерий для нескольких выборок Неравные доли цензурированных наблюдений Регрессионные модели Общее знакомство Модель пропорциональных интенсивностей Кокса Модель пропорциональных интенсивностей Кокса с зависящими от времени ковариатами Экспоненциальная регрессия Нормальная и логнормальная регрессия Стратифицированный анализ

 

Общие цели
Общие цели

Статистические методы, представленные в этом модуле, первоначально были развиты в медицинских, биологических исследованиях и страховании, но затем стали широко применяться в социальных и экономических науках, а также в инженерных задачах (анализ надежности и времен отказов).

Представьте, что вы изучаете эффективность нового метода лечения, применяемого в критической (терминальной) стадии заболевания (например, лечение новым методом практически неизлечимых больных). Наиболее важной, очевидно, переменной является продолжительность жизни пациентов с момента поступления в клинику. В принципе, для описания средних времен жизни и сравнения нового метода лечения со старыми, можно было бы использовать стандартные параметрические и непараметрические методы (см. Основные статистики и таблицы и Непараметрические статистики и распределения). Однако в анализируемых данных есть существенная особенность, связанная с тем, как вы строите выборку. При завершении вашего исследования могли найтись пациенты, которые выжили в течение всего периода наблюдения, в частности, среди тех, кто поступил в клинику позже других, а также пациенты, контакт с которыми был потерян до завершения эксперимента (например, их перевели в другие клиники). Естественно, вам не хотелось бы терять собранную о них информацию, поскольку большинство этих пациентов являются "выжившими" в течение того времени, которое вы их наблюдали, и тем самым свидетельствуют в пользу нового метода лечения. Наблюдения, которые содержат неполную информацию, называются цензурированными наблюдениями (например, "пациент A был жив, по крайней мере, 4 месяца до того, как был переведен в другую клинику и контакт с ним был потерян"). Использование в том числе и цензурированных наблюдений составляет специфику рассматриваемых здесь методов (термин цензурирование был впервые использован в работе Hald, 1949).

В начало

Цензурированные наблюдения
Цензурированные наблюдения

В общем, цензурированные наблюдения типичны, когда наблюдаемая величина представляет время до наступления некоторого критического события, а продолжительность наблюдения ограничена по времени. Цензурированные наблюдения встречаются во многих областях. Например, в социальных науках мы можем изучать "длительность" брака, интенсивность выбытия студентов из высшего учебного заведения (времен до выбытия), динамику численности работников в некоторых организациях и т.п.


В рассмотренных примерах в конце периода наблюдения некоторые субъекты остаются состоящими в браке, некоторые студенты продолжают учебу, а некоторые сотрудники продолжают работать в компании; таким образом, данные об этих субъектах являются цензурированными. Мы не можем дождаться того момента, когда все выбранные студенты покинут учебное заведение, а сотрудники компанию.

В экономике мы можем изучать "выживание" новых предприятий или времена "жизни" продуктов, таких как, например, автомобили. В задачах контроля качества типичным является изучение "выживания" элементов изделий под нагрузкой (анализ времен отказов). В актуарной математике в качестве объекта исследований обычно используют таблицы смертности, содержащие данные о смертности за выбранные интервалы времени лиц определенных категорий (например, мужчин старше 30 лет).

В начало

  Аналитические методы
Аналитические методы

Методы Анализа выживаемости в основном применяются к тем же статистическим задачам, что и другие методы, однако их особенность в том, что они применяются к цензурированным или, как иногда говорят, неполным данным. Отметим также, что более часто, чем обычная функция распределения, в этих методах используется так называемая функция выживания, представляющая собой вероятность того, что объект проживет время больше t. Построение таблиц времен жизни, подгонка распределения выживаемости, оценивание функции выживания с помощью процедуры Каплана-Мейера являются описательными методами исследования цензурированных данных. Некоторые из предложенных методов позволяют сравнивать выживаемость в двух и более группах. Наконец, Анализ выживаемости содержит регрессионные модели для оценивания зависимостей между многомерными непрерывными переменными со значениями типа времена жизни.

В начало

Анализ таблиц времен жизни
Анализ таблиц времен жизни

Наиболее естественным способом описания выживаемости в выборке явлвется построение Таблиц времен жизни. Техника таблиц времен жизни - один из старейших методов анализа данных о выживаемости (времен отказов) (см., например, работы Berkson and Gage, 1950; Cutler and Ederer, 1958; Gehan, 1969).


Такую таблицу можно рассматривать как "расширенную" таблицу частот. Область возможных времен наступления критических событий (смертей, отказов и др.) разбивается на некоторое число интервалов. Для каждого интервала вычисляется число и долю объектов, которые в начале рассматриваемого интервала были "живы", число и долю объектов, которые "умерли" в данном интервале, а также число и долю объектов, которые были изъяты или цензурированы в каждом интервале.

На основании этих величин вычисляются некоторые дополнительные статистики: Число изучаемых объектов Доля умерших Доля выживших Кумулятивная доля выживших (функция выживания) Плотность вероятности Функция интенсивности Медиана ожидаемого времени жизни Объем выборки
Число изучаемых объектов. Это число объектов, которые были "живы" в начале рассматриваемого временного интервала, минус половина числа изъятых или цензурированных объектов.

Доля умерших. Эта отношение числа объектов, умерших в соответствующем интервале, к числу объектов, изучаемых на этом интервале.

Доля выживших. Эта доля равна единице минус доля умерших.

Кумулятивная доля выживших (функция выживания). Это кумулятивная доля выживших к началу соответствующего временного интервала. Поскольку вероятности выживания считаются независимыми на разных интервалах, эта доля равна произведению долей выживших объектов по всем предыдущим интервалам. Полученная доля как функция от времени называется также выживаемостью или функцией выживания [точнее, это оценка функции выживания].

Плотность вероятности. Это оценка вероятности отказа в соответствующем интервале, определяемая таким образом::

Число изучаемых объектов. Это число объектов, которые были "живы" в начале рассматриваемого временного интервала, минус половина числа изъятых или цензурированных объектов.

Доля умерших. Эта отношение числа объектов, умерших в соответствующем интервале, к числу объектов, изучаемых на этом интервале.

Доля выживших. Эта доля равна единице минус доля умерших.



Кумулятивная доля выживших (функция выживания). Это кумулятивная доля выживших к началу соответствующего временного интервала. Поскольку вероятности выживания считаются независимыми на разных интервалах, эта доля равна произведению долей выживших объектов по всем предыдущим интервалам. Полученная доля как функция от времени называется также выживаемостью или функцией выживания [точнее, это оценка функции выживания].

Плотность вероятности. Это оценка вероятности отказа в соответствующем интервале, определяемая таким образом::

Fi = (Pi-Pi+1) /hi

где Fi - оценка вероятности отказа в i-ом интервале, Pi - кумулятивная доля выживших объектов (функция выживания) к началу i-го интервала, hi - ширина i-ого интервала.

Функция интенсивности. Функция интенсивности (этот термин был впервые использован в работе Barlow, 1963) определяется как вероятность того, что объект, выживший к началу соответствующего интервала, откажет или умрет в течение этого интервала. Оценка функции интенсивности вычисляется как число отказов, приходящихся на единицу времени соответствующего интервала, деленное на среднее число объектов, доживших до момента времени, находящегося в середине интервала.

Медиана ожидаемого времени жизни. Это точка на временной оси, в которой кумулятивная функция выживания равна 0.5. Другие процентили (например, 25- и 75-процентиль или квартили) кумулятивной функции выживания вычисляются по такому же принципу. Отмети, что 50-процентиль (медиана) кумулятивной функции выживаемости обычно не совпадает с точкой выживания 50% выборочных наблюдений. (Совпадение происходит только когда за прошедшее к этому моменту время не было цензурированных наблюдений).

Объем выборки. Чтобы получить надежные оценки трех основных функций (функции выживания, плотности вероятности и функции интенсивности) и их стандартных ошибок на каждом временном интервале, рекомендуется использовать не менее 30 наблюдений.

Функция интенсивности. Функция интенсивности (этот термин был впервые использован в работе Barlow, 1963) определяется как вероятность того, что объект, выживший к началу соответствующего интервала, откажет или умрет в течение этого интервала.


Оценка функции интенсивности вычисляется как число отказов, приходящихся на единицу времени соответствующего интервала, деленное на среднее число объектов, доживших до момента времени, находящегося в середине интервала.

Медиана ожидаемого времени жизни. Это точка на временной оси, в которой кумулятивная функция выживания равна 0.5. Другие процентили (например, 25- и 75-процентиль или квартили) кумулятивной функции выживания вычисляются по такому же принципу. Отмети, что 50-процентиль (медиана) кумулятивной функции выживаемости обычно не совпадает с точкой выживания 50% выборочных наблюдений. (Совпадение происходит только когда за прошедшее к этому моменту время не было цензурированных наблюдений).

Объем выборки. Чтобы получить надежные оценки трех основных функций (функции выживания, плотности вероятности и функции интенсивности) и их стандартных ошибок на каждом временном интервале, рекомендуется использовать не менее 30 наблюдений.

В начало

Подгонка распределения Общее знакомство Оценивание Согласие Графики
Общее знакомство.
Подгонка распределения Общее знакомство Оценивание Согласие Графики
Общее знакомство.

В общем случае таблица времен жизни дает хорошее представление о распределении отказов или смертей объектов во времени. Однако для прогноза часто необходимо знать форму рассматриваемой функции выживания. Наиболее важны следующие семейства распределений, которые используются для описания продолжительности жизни или наработки до отказа: экспоненциальное (в том числе, линейное экспоненциальное) распределение, распределение Вейбулла экстремальных значений и распределение Гомперца.

Оценивание. Процедура оценивания параметров использует алгоритм метода наименьших квадратов (см. работу Gehan and Siddiqui, 1973). Для проведения оценивания применима модель линейной регрессии, поскольку все четыре перечисленных семейства распределений могут быть "сведены к линейным" (относительно параметров) с помощью подходящих преобразований.


Такие преобразования приводят иногда к тому, что дисперсия остатков зависит от интервалов (т.е. дисперсия различная на различных интервалах). Чтобы учесть это, в алгоритмах подгонки используют оценки взвешенных наименьших квадратов двух типов.

Согласие. Зная параметрическое семейство распределений, можно вычислить функцию правдоподобия по имеющимся данным и найти ее максимум. Такие оценки называются оценками максимального правдоподобия. При весьма общих предположениях эти оценки совпадают с оценками наименьших квадратов. Аналогичным образом находится максимум функции правдоподобия при нулевой гипотезе, т.е. для модели, допускающей различные интенсивности на разных интервалах. Сформулированная гипотеза может быть проверена, например, с помощью критерия отношения правдоподобия, статистика которого имеет (по крайней мере, асимптотически) хи-квадрат распределение.

Графики. В модуле можно строить графики как эмпирических, так и теоретических функций распределения и интенсивности. Эти графики представляют собой прекрасное средство проверки согласия данных с теоретическим распределением. Ниже показана эмпирическая функция выживания и функции из семейства распределений Вейбулла. На этом графике три линии обозначают теоретические распределения, полученнные с помощью трех различных процедур оценивания (методом наименьших квадратов и двумя методами взвешенных наименьших квадратов).

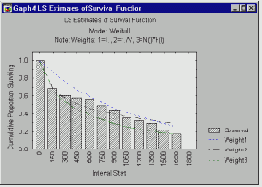
Множительные оценки Каплана-Мейера
Множительные оценки Каплана-Мейера

Для цензурированных, но не группированных наблюдений времен жизни, функцию выживания можно оценить непосредственно (без таблицы времен жизни). Представьте, что вы создали файл, в котором каждое наблюдение содержит точно один временной интервал. Перемножая вероятности выживания в каждом интервале, получим следующую формулу для функции выживания:

S(t) = jt= 1 [(n-j)/(n-j+1)]( j )

В этом выражении S(t) - оценка функции выживания, n - общее число событий (времен окончания), j - порядковый (хронологически) номер отдельного события, d(j) равно 1, если j-ое событие означает отказ (смерть) и (j) равно 0, если j-ое событие означает потерю наблюдения (цензурирование). означает произведение по всем наблюдениям j, завершившимся к моменту t.


Данная оценка функции выживания, называемая множительной оценкой, впервые была предложена Капланом и Мейером (1958).



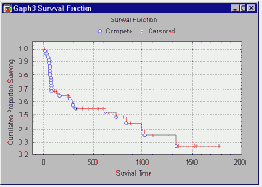
Преимущество метода Каплана-Мейера (по сравнению с методом таблиц жизни) состоит в том, что оценки не зависят от разбиения времени наблюдения на интервалы, т.е. от группировки. Метод множительных оценок и метод таблиц времен жизни приводят, по существу, к одинаковым результатам, если временные интервалы содержат, максимум, по одному наблюдению.

В начало

  Сравнение выборок Общее знакомство Доступные критерии Выбор двухвыборочного критерия Критерий для нескольких выборок Неравные доли цензурированных наблюдений

Общее знакомство.
Сравнение выборок Общее знакомство Доступные критерии Выбор двухвыборочного критерия Критерий для нескольких выборок Неравные доли цензурированных наблюдений

Общее знакомство.

Можно сравнить времена жизни или, на техническом языке, наработки до отказа нескольких выборок. В принципе, т.к. времена жизни не являются нормально распределенными, можно использовать непараметрические тесты, основанные на рангах. Непараметрические статистики предлагают широкий набор непараметрических критериев, которые могли бы быть применены для сравнения времен жизни; однако эти критерии не "работают" с цензурированными данными.

Доступные критерии. В Анализе выживаемости имеется пять различных (в основном непараметрических) критериев для цензурированных данных: обобщенный (Геханом) критерий Вилкоксона, F-критерий Кокса, логарифмический ранговый критерий, а также обобщенный Пето (Peto R.и Peto J.) критерий Вилкоксона. Большинство этих критериев приводят соответствующие z-значения (значения стандартного нормального распределения); эти z-значения могут быть использованы для статистической проверки любых различий между группами. Однако критерии дают надежные результаты лишь при достаточно больших объемах выборок. При малых объемах выборок их "поведение" менее поддается осмыслению.

Выбор двухвыборочного критерия. Не существует твердо установленных рекомендаций по применению определенных критериев.


Однако известно, что F - критерий Кокса обычно более мощный, чем критерий Вилкоксона - Гехана, если: выборочные объемы малы (то есть объем группы n меньше 50); если выборки извлекаются из экспоненциального распределения или распределения Вейбулла; если нет цензурированных наблюдений (см. работу Gehan and Thomas, 1969). В работе Lee, Desu, and Gehan (1975) авторы сравнили критерий Гехана с некоторыми другими критериями и показали, что критерий Кокса-Ментела и логарифмически ранговый критерий являются более мощным (безотносительно к цензурированию), если выборки извлечены из экспоненциального распределения или распределения Вейбулла; при этих условиях между критерием Кокса-Ментела и логарифмически ранговым критерием почти нет различия. В работе Ли (Lee (1980)) обсуждается мощность различных критериев более детально. Если вас затрудняет выбор определенного критерия, мы рекомендуем обратиться к этим работам.

Критерий для нескольких выборок.
Критерий для нескольких выборок.

Многовыборочный критерий представляет собой развитие критерия Вилкоксона, обобщенного Геханом, критерия Вилкоксона, обобщенного Пето, и логарифмически рангового критерия. Сначала каждому времени жизни приписывается его вклад в соответствии с процедурой Ментела (Mantel, 1967); далее на основе этих вкладов (по группам) вычисляется значение статистики хи-квадрат. Если выделены только две группы, то критерий эквивалентен критерию Вилкоксона, обобщенному Геханом.

Неравные доли цензурированных наблюдений.

Неравные доли цензурированных наблюдений.

Если сравниваются две или более группы, то важно проверить доли цензурированных наблюдений в каждой. В частности, в медицинских исследованиях степень цензурирования может зависеть, например, от различий в методе лечения: пациенты, которым стало много лучше или стало хуже, с большой вероятностью теряются из наблюдения. Различие в степени цензурирования может привести к смещению в статистических выводах.

В начало

Регрессионные модели Общее знакомство Модель пропорциональных интенсивностей Кокса Модель пропорциональных интенсивностей Кокса с зависящими от времени ковариатами Экспоненциальная регрессия Нормальная и логнормальная регрессия Стратифицированный анализ  




Общее знакомство
Общее знакомство

Самая большая проблема медицинских, биологических или инженерных статистических исследований состоит в выяснении того, являются ли некоторые непрерывные переменные связанными с наблюдаемыми временами жизни. Есть две главные причины, по которым в таких исследованиях не может быть непосредственно применена классическая техника множественной регрессии (см. Множественная регрессия). Во-первых, времена жизни обычно не являются нормально распределенными, а это является серьезным нарушением предположений для оценивания множественной регрессии по методу наименьших квадратов. Времена жизни обычно имеют экспоненциальное распределение или распределение Вейбулла. Во-вторых имеется проблема с цензурированными, т.е. незавершенными наблюдениями.




Модель пропорциональных интенсивностей Кокса
Модель пропорциональных интенсивностей Кокса

Модель пропорциональных интенсивностей - наиболее общая регрессионная модель, поскольку она не связана с какими-либо предположениями относительно распределения времени выживания. Эта модель предполагает, что функция интенсивности имеет некоторый уровень y, являющийся функцией независимых переменных. Никаких предположений о виде функции интенсивности не делается. Поэтому модель Кокса может рассматриваться как в некотором смысле непараметрическая. Модель может быть записана в следующем виде:

h{(t), (z1, z2, ..., zm)} = h0(t)*exp(b1*z1 + ... + bm*zm)

где h(t,...) обозначает результирующую интенсивность, при заданных для соответствующего наблюдения значениях m ковариат (z1, z2, ..., zm) и соответствующем времени жизни (t). Множитель h0(t) называется базовой функцией интенсивности, она равна интенсивности в случае, когда все независимые переменные равны нулю. Можно линеаризовать эту модель, поделив обе части соотношения на h0(t) и взяв натуральный логарифм от обеих частей:

log[h{(t), (z...)}/h0(t)] = b1*z1 + ... + bm*zm

Теперь мы имеем достаточно "простую" линейную модель, которая легко поддается изучению.



Предположения.
Предположения.

В то время как никаких прямых предположений о виде функции интенсивности ранее не делалось, модельное уравнение, приведенное выше, подразумевает два предположения. Во-первых, зависимость между функцией интенсивности и логлинейной функцией ковариат является мультипликативной. Это соотношение называется также предположением (гипотезой) пропорциональности. Реально оно означает, что для двух заданных наблюдений с различными значениями независимых переменных отношения их функций интенсивности не зависит от времени (чтобы ослабить это предположение, используются ковариаты, зависящие от времени; см. ниже). Второе предположение состоит именно в логарифмической линейности соотношения между функцией интенсивности и независимыми переменными.




Модель пропорциональных интенсивностей Кокса с зависящими от времени ковариатами
Модель пропорциональных интенсивностей Кокса с зависящими от времени ковариатами

Обоснованность предположения пропорциональности интенсивности часто подвергается сомнению. Например, рассмотрим гипотетическое исследование, в котором ковариатой является категориальная (групповая) переменная, а именно, индикатор того, подвергнут некоторый пациент или нет хирургической операции. Пусть пациент 1 подвергнут операции, в то время как пациент 2 - нет. Согласно предположению пропорциональности отношение функций интенсивностей для обоих пациентов не зависит от времени и означает, что риск для пациента, подвергнутого операции, постоянно более высокий (или более низкий), чем риск пациента, не подвергнутого операции (при условии, что оба дожили до рассматриваемого момента). Однако обычно более реалистична другая модель, а именно: сразу после операции риск прооперированного пациента выше, однако при благоприятном исходе операции с течением времени убывает и становится меньше риска не оперированного пациента. В этом случае предпочтительнее ковариаты, зависящие от времени. Можно привести много других примеров, где предположение о пропорциональности неприемлемо.


Так, при изучении физического здоровья возраст является одним из факторов выживаемости после хирургической операции. Ясно, что возраст - более важный предиктор для риска сразу после операции, чем по прошествии некоторого времени после операции (например, после первых признаков выздоровления). В ускоренных испытаниях на надежность иногда используют нагрузочную ковариату (например, уровень напряжения), которую медленно наращивают со временем вплоть до отказа прибора, например, до пробоя изоляции; см. Lawless, 1982, стр. 393). В этом случае влияние ковариаты опять зависит от времени.

Проверка предположения пропорциональности.
Проверка предположения пропорциональности.

Как отмечалось в предыдущих примерах, часто предположение пропорциональности не выполняется. В таком случае, можно явно определить ковариаты, как функции времени. Например, рассмотрим набор данных, представленных Pike (1966), который состоит из времен жизни двух групп крыс, одна из которых была контрольной, а другая была подвергнута воздействию канцерогена (см. также подобный пример в работе Lawless, 1982, стр. 393). Предположим, что z - групповая переменная со значениями 1 и 0 для подвергнутых воздействию и контрольных крыс соответственно. Тогда можно проводить подгонку функции интенсивности с помощью модели пропорциональных интенсивностей вида:

h(t,z) = h0(t)*exp{b1*z + b2*[z*log(t)-5.4]}

Обратите внимание, что функция интенсивности в момент t есть функция: (1) базовой функции интенсивности h0, (2) ковариаты z и (3) z-кратного логарифма времени. Заметим, что константа 5.4 использована здесь только как нормировка, т.к. среднее логарифма времени жизни для этого множества данных равно 5.4. Другими словами, структурированный моделью множитель с ковариатами в каждый момент времени есть функция ковариаты и времени; таким образом, влияние ковариаты на выживаемость зависит от времени; отсюда название - ковариата, зависящая от времени. Эта модель позволяет использовать специфический критерий проверки предположения пропорциональности.


Если параметр b2 статистически значим (например, если он, по крайней мере, в два раза больше своей стандартной ошибки), то можно сделать вывод, что ковариаты z действительно зависят от времени, и поэтому предположение пропорциональности не выполняется.

Экспоненциальная регрессия
Экспоненциальная регрессия

В своей основе эта модель предполагает, что распределение продолжительности жизни является экспоненциальным и связано со значениями некоторого множества независимых переменных (zi). Параметр интенсивности экспоненциального распределения выражается в виде:

S(z) = exp(a + b1*z1 + b2*z2 + ... + bm*zm)

Здесь S(z) обозначает время жизни, a - константа, а bi - параметры регрессии.

Согласие.
Согласие.

Значение критерия хи-квадрат может быть вычислено как функция логарифма правдоподобия для модели со всеми оцененными параметрами (L1) и логарифма правдоподобия модели, в которой все ковариаты обращаются в 0 (L0). Если значение хи-квадрат статистически значимо, отвергаем нулевую гипотезу и принимаем, что независимые переменные значимо влияют на время жизни.

Стандартная экспоненциальная порядковая статистика.
Стандартная экспоненциальная порядковая статистика.

Один из способов проверки предположения экспоненциальности - построение остатков времен жизни и сравнение их со значениями стандартных экспоненциальных порядковых статистик альфа.




Нормальная и логнормальная регрессия
Нормальная и логнормальная регрессия

В этой модели предполагается, что времена жизни (или их логарифмы) имеют нормальное распределение. Модель в основном идентична обычной модели множественной регрессии и может быть описана следующим образом:

t = a + b1*z1 + b2*z2 + ... + bm*zm

Здесь t означает время жизни. Если принимается модель логнормальной регрессии, то t заменяется ln t. Модель нормальной регрессии особенно полезна, поскольку часто данные могут быть преобразованы в нормальные применением нормализующих аппроксимаций. Таким образом, в некотором смысле это наиболее общая параметрическая модель (в противоположность модели пропорциональных интенсивностей Кокса, которая является непараметрической), оценки которой могут быть получены для большого разнообразия исходных распределений времен жизни.



Согласие.
Согласие.

Значение хи-квадрат может быть вычислено как функция логарифма правдоподобия для модели со всеми независимыми переменными (L1) логарифма правдоподобия для модели, в которой все независимые переменные заменены 0 (L0).




Стратифицированный анализ
Стратифицированный анализ

Цель стратифицированного анализа - проверить гипотезу о том, что одна и та же регрессия является подходящей для разных групп (данных); то есть зависимость между выживаемостью и регрессорами одна и та же для разных групп данных. При стратифицированном анализе Анализ выживаемости вначале строит регрессионные модели отдельно для каждой группы. Сумма логарифмов правдоподобия для разных моделей представляет собой логарифм правдоподобия модели с разными коэффициентами регрессии (и свободными членами, если требуется) в разных группах. Далее программа подгоняет требуемую регрессионную модель ко всем данным обычным образом, не учитывая разбиение на группы, и вычисляет общий логарифм правдоподобия. По разности этих двух логарифмов правдоподобия проверяется статистическая значимость различия между группами (с точки зрения хи-квадрат статистики).


(c) Copyright StatSoft, Inc., 1984-2001
STATISTICA является торговой маркой StatSoft, Inc.

Деревья классификации

Деревья классификации

Основные идеи Характеристики деревьев классификации Иерархическая природа деревьев классификации Гибкость метода деревьев классификации Сила и слабости метода деревьев классификации Вычислительные методы Выбор критерия точности прогноза Выбор типа ветвления Определение момента прекращения ветвлений Определение "подходящих" размеров дерева Сравнение с другими программами построения деревьев классификации

Основные идеи
Основные идеи Характеристики деревьев классификации Иерархическая природа деревьев классификации Гибкость метода деревьев классификации Сила и слабости метода деревьев классификации Вычислительные методы Выбор критерия точности прогноза Выбор типа ветвления Определение момента прекращения ветвлений Определение "подходящих" размеров дерева Сравнение с другими программами построения деревьев классификации

Основные идеи

Деревья классификации - это метод, позволяющий предсказывать принадлежность наблюдений или объектов к тому или иному классу категориальной зависимой переменной в зависимости от соответствующих значений одной или нескольких предикторных переменных. Построение деревьев классификации - один из наиболее важных методов, используемых при проведении "добычи данных".

Цель построения деревьев классификации заключается в предсказании (или объяснении) значений категориальной зависимой переменной, и поэтому используемые методы тесно связаны с более традиционными методами Дискриминантного анализа, Кластерного анализа, Непараметрической статистики и Нелинейного оценивания. Широкая сфера применимости деревьев классификации делает их весьма привлекательным инструментом анализа данных, но не следует поэтому полагать, что его рекомендуется использовать вместо традиционных методов статистики. Напротив, если выполнены более строгие теоретические предположения, налагаемые традиционными методами, и выборочное распределение обладает некоторыми специальными свойствами, то более результативным будет использование именно традиционных методов.
Однако, как метод разведочного анализа, или как последнее средство, когда отказывают все традиционные методы, деревья классификации, по мнению многих исследователей, не знают себе равных.

Что же такое деревья классификации? Представьте, что вам нужно придумать устройство, которое отсортирует коллекцию монет по их достоинству (например, 1, 2, 3 и 5 копеек). Предположим, что какое-то из измерений монет, например - диаметр, известен и, поэтому, может быть использован для построения иерархического устройства сортировки монет. Заставим монеты катиться по узкому желобу, в котором прорезана щель размером с однокопеечную монету. Если монета провалилась в щель, то это 1 копейка; в противном случае она продолжает катиться дальше по желобу и натыкается на щель для двухкопеечной монеты; если она туда провалится, то это 2 копейки, если нет (значит это 3 или 5 копеек) - покатится дальше, и так далее. Таким образом, мы построили дерево классификации. Решающее правило, реализованное в этом дереве классификации , позволяет эффективно рассортировать горсть монет, а в общем случае применимо к широкому спектру задач классификации.

Изучение деревьев классификации не слишком распространено в вероятностно-статистическом распознавании образов (см. работу Ripley, 1996), однако они широко используются в таких прикладных областях, как медицина (диагностика), программирование (анализ структуры данных), ботаника (классификация) и психология (теория принятия решений). Деревья классификации идеально приспособлены для графического представления, и поэтому сделанные на их основе выводы гораздо легче интерпретировать, чем если бы они были представлены только в числовой форме.

Деревья классификации могут быть, а иногда и бывают очень сложным. Однако использование специальных графических процедур, позволяет упростить интерпретацию результатов даже для очень сложных деревьев. Если пользователя интересуют прежде всего условия попадания объекта в один определенный класс, например, в класс с высоким уровнем отклика, он может обратиться к специальной дискретной Карте линий уровня , показывающей, к какой из терминальных вершин дерева классификации отнесены большинство наблюдений с высоким уровнем отклика.





В примере, показанном на этой Карте линий уровня , мы можем мысленно "пройти" по ветвям дерева, ведущим к терминальной вершине 8, чтобы понять, при каких условиях достигается высокий уровень отклика.

Возможность графического представления результатов и простота интерпретации во многом объясняют большую популярность деревьев классификации в прикладных областях, однако наиболее важными отличительными свойствами деревьев классификации является их иерархичность и широкая применимость.

Вычислительные аспекты методов деревьев классификации описаны в разделе Вычислительные методы. См. также раздел Методы разведочного анализа данных.

В начало

Характеристики деревьев классификации

Иерархическая природа деревьев классификации
Иерархическая природа деревьев классификации

В книге Breiman et al. (1984) приводится ряд примеров применения деревьев классификации. Один из них посвящен диагностике больных, поступающих в стационар с сердечным приступом. В приемном отделении у них измеряют несколько десятков показателей (частоту пульса, кровяное давление и т.д.). Одновременно в базу данных заносится много другой информации о больном (возраст, перенесенные болезни и др.). Из последующей истории пациента можно, в частности, выделить такой показатель: прожил ли он 30 дней (или более) после приступа. Для разработки методов лечения больных с сердечной недостаточностью, а также для развития разделов медицинской науки, касающихся болезней сердца, было бы весьма полезно научиться по данным первичного обследования выявлять пациентов с высокой степенью риска (тех, кто, вероятнее всего, не сможет прожить больше 30 дней). Одно из деревьев классификации , построенных авторами для этой задачи, представляло собой довольно простое дерево решений с тремя вопросами. На словах это бинарное дерево классификации можно описать следующей фразой: "Если нижнее давление у пациента в течение первых суток не опускается ниже 91, то, если его возраст превосходит 62.5 года, то, если у него наблюдается синусоидальная тахикардия, то в этом и только в этом случае следует ожидать, что пациент не сможет прожить 30 дней." Из этого предложения несложно представить себе соответствующее "дерево" решений.


Вопросы задаются последовательно (иерархически), и окончательное решение зависит от ответов на все предыдущие вопросы. Это похоже на то, как положение листа на дереве можно задать, указав ведущую к нему последовательность ветвей (начиная со ствола и кончая самой последней веточкой, на которой лист растет). Иерархическое строение дерева классификации - одно из наиболее важных его свойств (не следует, однако, чересчур буквально принимать аналогию между ним и настоящим деревом; деревья решений чаще всего рисуются на бумаге вверх ногами, так что если уж искать аналогии в живой природе, то придется обратиться к такому мало поэтичному образу, как корневая система растения).

Иерархическую структуру дерева классификации легко себе уяснить, сравнив используемую там процедуру принятия решения с тем, что происходит при проведении Дискриминантного анализа. Классический линейный дискриминантный анализ данных по сердечной недостаточности выдал бы набор коэффициентов, задающих одну, вполне определенную линейную комбинацию показателей кровяного давления, возраста и данных о синусовой тахикардии, которая наилучшим образом отделяет пациентов с высоким уровнем риска от остальных. Значение дискриминантной функции для каждого пациента будет вычисляться как комбинация результатов измерений трех предикторных переменных с весами, которые задаются соответствующими коэффициентами дискриминантной функции. При классификации данного пациента как имеющего высокий (низкий) уровень риска принимаются в расчет одновременно значения всех трех предикторных переменных. Пусть, например, предикторные переменные обозначаются через P (минимальное за последние сутки систолическое кровяное давление), A (возраст) и T (наличие синусоидальной тахикардии: 0 = нет; 1 = есть), p, a и t - соответствующие им весовые коэффициенты в дискриминантной функции, а c - "пороговое значение" дискриминантной функции, разделяющее пациентов на два класса. Решающее правило будет тогда иметь вид "если для данного пациента pP + aA + tT - c меньше или равно нулю, то у него низкий уровень риска, иначе - высокий уровень риска."



В случае же с решающим деревом, построенным в Breiman et al. (1984), процедура будет иметь следующий, иерархический, вид: пусть значения p, a и t равны соответственно -91, -62.5 и 0, тогда правило формулируется так: "Если p + P меньше или равно нулю, то у пациента низкий уровень риска, иначе если a + A меньше или равно нулю, то у пациента низкий уровень риска, иначе если t + T меньше или равно нулю, то у пациента низкий уровень риска, иначе у пациента высокий уровень риска." На первый взгляд, процедуры принятия решения Дискриминантного анализа и деревьев классификации выглядят похожими, так в обеих участвуют решающие уравнения и коэффициенты. Однако имеется принципиальное различие между одновременным принятием решения в Дискриминантном анализе и последовательным (иерархическим) в деревьях классификации.

Различие между этими двумя подходами станет яснее, если посмотреть, как в том и другом случае выполняется Регрессия. В рассматриваемом примере риск представляет собой дихотомическую зависимую переменную, и прогнозирование с помощью Дискриминантного анализа осуществляется путем одновременной множественной регрессии риска на три предикторных переменных для всех пациентов. С другой стороны, прогнозирование методом деревьев классификации состоит из трех отдельных этапов простого регрессионного анализа: сначала берется регрессия риска на переменную P для всех пациентов, затем - на переменную A для тех пациентов, которые не были классифицированы как низкорисковые на первом шаге регрессии, и, наконец - на переменную T для пациентов, не отнесенных к низкорисковым на втором шаге. Здесь отчетливо проявляются различие одновременного принятия решения в Дискриминантном анализе и последовательного (рекурсивного, иерархического) -- в деревьях классификации. Эта характеристика деревьев классификации имеет далеко идущие последствия.

Гибкость метода деревьев классификации
Гибкость метода деревьев классификации

Другая отличительная черта метода деревьев классификации - это присущая ему гибкость.


Мы уже сказали о способности деревьев классификации последовательно изучать эффект влияния отдельных переменных. Есть еще целый ряд причин, делающих деревья классификации более гибким средством, чем традиционные методы анализа. Способность деревьев классификации выполнять одномерное ветвление для анализа вклада отдельных переменных дает возможность работать с предикторными переменными различных типов. В примере с сердечными приступами, рассмотренном в работе Breiman et al. (1984), давление и возраст являются непрерывными, а наличие/отсутствие синусоидальной тахикардии - категориальной (двухуровневой) предикторной переменной. Простое разветвление предиктора можно было бы выполнить, даже если бы тахикардия измерялась по трехуровневой категориальной шкале (например: 0 = отсутствует; 1 = присутствует; 3 = неизвестно или показания неясны). Если новая категория содержит какую-то дополнительную информацию о риске, то к дереву решений можно добавить новые узлы, учитывающие и использующие эту информацию. Таким образом, при построении одномерных ветвлений деревья классификации позволяют использовать для ветвления как непрерывные, так и категориальные переменные.

В классическом линейном дискриминантном анализе требуется, чтобы предикторные переменные были измерены как минимум в интервальной шкале. В случае же деревьев классификации с одномерным ветвлением по переменным, измеренным в порядковой шкале, любое монотонное преобразование предикторной переменной (т.е. любое преобразование, сохраняющее порядок в значениях переменной) создаст ветвление на те же самые предсказываемые классы объектов (наблюдений) (если используется Одномерное ветвление по методу CART, смотрите Breimen и др., 1984). Поэтому дерево классификации на основе одномерного ветвления можно строить независимо от того, соответствует ли единичное изменение непрерывного предиктора единичному изменению лежащей в его основе величины или нет, достаточно, чтобы предикторы были измерены в порядковой шкале. Иными словами, на способ измерения предикторной переменной накладываются гораздо более слабые ограничения.



Деревья классификации не ограничены использованием только одномерных ветвлений по предикторным переменным. Если непрерывные предикторы измерены хотя бы в интервальной шкале, то деревья классификации могут использовать ветвления по линейным комбинациям, подобно тому, как это делается в линейном дискриминантном анализе. При этом ветвления по линейным комбинациям, применяемые для построения деревьев классификации, имеют ряд важных отличий от своих аналогов из дискриминантного анализа. В линейном дискриминантном анализе максимальное количество линейных дискриминантных функций равно минимуму из числа предикторных переменных и числа классов зависимой переменной минус один. При рекурсивном подходе, который используется в модуле Деревья классификации, мы не связаны этим ограничением. Например, для десяти предикторных переменных и всего двух классов зависимой переменной мы можем использовать десятки последовательных ветвлений по линейным комбинациям. Это выгодно отличается от единственного ветвления по линейной комбинации, предлагаемого в данном случае традиционным нерекурсивным линейным дискриминантным анализом. При этом значительная часть информации, содержащейся в предикторных переменных, может остаться неиспользованной.

Рассмотрим теперь ситуацию, когда имеется много категорий, но мало предикторов. Предположим, например, что мы хотим рассортировать монеты различных достоинств, имея только данные измерений их толщины и диаметра. В обычном линейном дискриминантном анализе можно получить самое большее две дискриминантных функции, и монеты могут быть успешно рассортированы только в том случае, если они различаются не более чем двумя параметрами, представимыми в виде линейных комбинаций толщины и диаметра монеты. Напротив, в подходе, который используется в модуле Деревья классификации, мы не связаны ограничениями в количестве ветвлений по линейным комбинациям, которое можно проделать.

Аппарат ветвления по линейным комбинациям, реализованный в модуле Деревья классификации, может быть использован также как метод анализа при построении деревьев классификации с одномерным ветвлением.


На самом деле одномерное ветвление есть частный случай ветвления по линейной комбинации. Представьте себе такое ветвление по линейной комбинации, при котором весовые коэффициенты при всех предикторных переменных, кроме какой-то одной, равны нулю. Поскольку значение комбинации фактически зависит от значений только одной предикторной переменной (коэффициент при которой отличен от нуля), полученное в результате этого ветвление будет одномерным.

Реализованные в модуле Деревья классификации методы дискриминантного Одномерного ветвления по категориальным и порядковым предикторам и дискриминантного Многомерного ветвления по линейным комбинациям порядковых предикторов представляют собой адаптацию соответствующих алгоритмов пакета QUEST (Quick, Unbiased, Efficient Statistical Trees). QUEST - это программа деревьев классификации, разработанная Loh и Shih (1997), в которой используются улучшенные варианты метода рекурсивного квадратичного дискриминантного анализа и которая содержит ряд новых средств для повышения надежности и эффективности деревьев классификации, которые она строит.

Алгоритмы пакета QUEST довольно сложны (ссылки на источники, где имеются описания алгоритмов, см. в разделе Замечания о вычислительных алгоритмах), однако в модуле Деревья классификации имеется опция Тип ветвления, предоставляющая пользователю другой, концептуально более простой подход. Реализованный здесь алгоритм Одномерного ветвления по методу CART является адаптацией алгоритмов пакета CART, см. Breiman и др. (1984). CART (Classification And Regression Trees) - это программа деревьев классификации, которая при построении дерева осуществляет полный перебор всех возможных вариантов одномерного ветвления.

Опции анализа QUEST и CART естественно дополняют друг друга. В случаях, когда имеется много предикторных переменных с большим числом уровней, поиск методом CART может оказаться довольно продолжительным. Кроме того, этот метод имеет склонность выбирать для ветвления те предикторные переменные, у которых больше уровней.


Однако поскольку здесь производится полный перебор вариантов, есть гарантия, что будет найден вариант ветвления, дающий наилучшую классификацию (по отношению к обучающей выборке; вообще говоря, это необязательно будет так для кросс-проверочных выборок).

Метод QUEST - быстрый и несмещенный. Его преимущество в скорости перед методом CART становится особенно заметным, когда предикторные переменные имеют десятки уровней (см. Loh & Shih, 1997, где приводится пример, когда метод QUEST потребовал 1 секунды времени процессора, а CART - 30.5 часов). Отсутствие у метода QUEST смещения в выборе переменных для ветвления также является его существенным преимуществом в случаях, когда одни предикторные переменные имеют мало уровней, а другие - много (предикторы со многими уровнями часто порождают "методы тыка", которые хорошо согласуются с данными, но дают плохую точность прогноза, см. Doyle, 1973, и Quinlan & Cameron-Jones, 1995). Наконец, метод QUEST не жертвует точностью прогноза ради скорости вычислений (Lim, Loh, & Shih, 1997). Сочетание опций QUEST и CART позволяет полностью использовать всю гибкость аппарата деревьев классификации.

Сила и слабости метода деревьев классификации
Сила и слабости метода деревьев классификации

Преимущества (по крайней мере, для некоторых областей применения) метода деревьев классификации перед такими традиционными методами, как линейный дискриминантный анализ, можно проиллюстрировать на простом условном примере. Чтобы соблюсти объективность, мы затем рассмотрим примеры с другим набором данных, где методы линейного дискриминантного анализа превосходят метод деревьев классификации.

Предположим, что у Вас имеются данные о координатах - Долготе - Longitude и Широте - Latitude - для 37 циклонов, достигающих силы урагана, по двум классификациям циклонов - Baro и Trop. Приведенный ниже модельный набор данных использовался для целей иллюстрации в работе Elsner, Lehmiller, и Kimberlain (1996), авторы которой исследовали различия между бароклинными и тропическими циклонами в Северной Атлантике.



ДАННЫЕ: Barotrop.sta 3v LONGITUD LATITUDE CLASS

59.00 59.50 60.00 60.50 61.00 61.00 61.50 61.50 62.00 63.00 63.50 64.00 64.50 65.00 65.00 65.00 65.50 65.50 65.50 66.00 66.00 66.00 66.50 66.50 66.50 67.00 67.50 68.00 68.50 69.00 69.00 69.50 69.50 70.00 70.50 71.00 71.50	17.00 21.00 12.00 16.00 13.00 15.00 17.00 19.00 14.00 15.00 19.00 12.00 16.00 12.00 15.00 17.00 16.00 19.00 21.00 13.00 14.00 17.00 17.00 18.00 21.00 14.00 18.00 14.00 18.00 13.00 15.00 17.00 19.00 12.00 16.00 17.00 21.00	BARO BARO BARO BARO BARO BARO BARO BARO BARO TROP TROP TROP TROP TROP TROP TROP TROP TROP TROP TROP TROP TROP TROP TROP TROP TROP TROP BARO BARO BARO BARO BARO BARO BARO BARO BARO BARO

Линейный дискриминантный анализ циклонов на предмет их принадлежности к Классу - Baro или Trop на основе данных о Долготе и Широте в качестве предикторов позволил правильно классифицировать только 20 наблюдений из 37 (54%). Дерево классификации для переменной Class, использующее опцию Полный перебор деревьев с одномерным ветвлением по методу CART сумело правильно классифицировать все 37 циклонов. Граф дерева для этого дерева классификации показан ниже.



В заголовке графа приведена общая информация, согласно которой полученное дерево классификации имеет 2 ветвления и 3 терминальные вершины. Терминальные вершины (или, как их иногда называют, листья) это узлы дерева, начиная с которых никакие решения больше не принимаются. На рисунке терминальные вершины показаны красными пунктирными линиями, а остальные - так называемые решающие вершины или вершины ветвления - сплошными черными линиями. Началом дерева считается самая верхняя решающая вершина, которую иногда также называют корнем дерева. На рисунке она расположена в левом верхнем углу и помечена цифрой 1. Первоначально все 37 циклонов приписываются к этой корневой вершине и предварительно классифицируются как Baro - на это указывает надпись Baro в правом верхнем углу вершины.


Класс Baro был выбран для начальной классификации потому, что число циклонов Baro немного больше, чем циклонов Trop (см. гистограмму, изображенную внутри корневой вершины). В левом верхнем углу графа имеется надпись - легенда , указывающая, какие столбики гистограммы вершины соответствуют циклонам Baro и Trop.

Корневая вершина разветвляется на две новых вершины. Под корневой вершиной имеется текст, описывающий схему данного ветвления. Из него следует, что циклоны, имеющие значение Долготы меньшее или равное 67.75, отнесены к вершине номер 2 и предположительно классифицированы как Trop, а циклоны с Долготой, большей 67.75 приписаны к вершине 3 и классифицированы как Baro. Числа 27 и 10 над вершинами 2 и 3 соответственно обозначают число наблюдений, попавших в эти две дочерние вершины из родительской корневой вершины. Затем точно так же разветвляется вершина 2. В результате 9 циклонов со значениями Долготы меньшими или равными 62.5 приписываются к вершине 4 и классифицируются как Baro, а остальные 18 циклонов с Долготой, большей 62.5, - к вершине 5 и классифицируются как Trop.

На Графе дерева вся эта информация представлена в простом, удобном для восприятия виде, так что для ее понимания требуется гораздо меньше времени, чем его ушло у Вас на чтение двух последних абзацев. Если теперь мы посмотрим на гистограммы терминальных вершин дерева, расположенных в нижней строке, то увидим, что дерево классификации сумело абсолютно правильно расклассифицировать циклоны. Каждая из терминальных вершин "чистая", то есть не содержит неправильно классифицированных наблюдений. Вся информация, содержащаяся в Графе дерева, продублирована в таблице результатов Структура дерева, которая приведена ниже.

Таблица 1
Таблица 1

Структура дерева (barotrop.sta) ДЕРЕВЬЯ
КЛАССИФИКАЦИИ Дочерние вершины, наблюдаемые,
предсказанный класс, условия ветвления  
Вершина Левая
вершина Правая
вершина Класс
BARO Класс
TROP Предсказ.
класс Ветвл. по
констант. Ветвл. по
перемен. 1
2
3
4
5

2 4	3 5	19   9 10   9   0	18 18   0   0 18	BARO TROP BARO BARO TROP	-67.75 -62.50	LONGITUD LONGITUD

Обратите внимание на то, что в этой таблице результатов вершины с 3-й по 5-ю помечены как терминальные, так как в них не происходит ветвления. Обратите также внимание на знаки Постоянных ветвления - например -67.75 для вершины 1. В Графе дерева условие ветвления в вершине 1 записано как LONGITUD  67.75 вместо эквивалентного -67.75 + LONGITUD 0. Это сделано просто для экономии места на рисунке.

Если делаются одномерные ветвления, то каждой предикторной переменной можно приписать ранг по шкале от 0 до 100 в зависимости от степени ее влияния на отклик зависимой переменной. В нашем примере очевидно, что Долгота - Longitude имеет большую важность, а Широта - Latitude - относительно небольшую.



Дерево классификации для переменной Класс - Class, построенное с использованием Дискриминантных одномерных ветвлений, дает почти такие же результаты. В приведенной ниже таблице результатов Структура дерева для этого варианта анализа константы ветвления равны -63.4716 и -67.7516 - то есть почти те же, что получились в варианте Полного перебора деревьев с одномерным ветвлением по методу CART . Здесь, однако, один циклон класса Trop в терминальной вершине 2 неправильно классифицирован как Baro.

Таблица 2
Таблица 2

Структура дерева (barotrop.sta) ДЕРЕВЬЯ
КЛАССИФИКАЦИИ Дочерние вершины, наблюдаемые,
предсказанный класс, условия ветвления  
Node Левая
вершина Правая
вершина Класс
BARO Класс
TROP Предсказ.
класс Ветвл. по
констант. Ветвл. по
перемен. 1
2
3
4
5

2   4	3   5	19   9 10   0 10	18   1 17 17 0	BARO BARO TROP TROP BARO	-63.4716   -67.7516	LONGITUD   LONGITUD

Категоризованный точечный график для переменных Долгота - Longitude и Широта - Latitude ясно показывает, почему линейный дискриминантный анализ так позорно провалился в задаче предсказания переменной Class и почему дерево классификации дает такие хорошие результаты.



 

График ясно показывает, что нет отчетливой линейной связи между переменными широты, долготы или какой-либо их линейной комбинацией с одной стороны, и переменной Class - с другой. Переменная Class функционально не связана с долготой и широтой, по крайней мере, в линейном смысле. На графике показана попытка ветвления посредством LDF (линейной дискриминантной функции): циклоны, относительно которых делается прогноз Trop, находятся над линией ветвления, а прогнозируемые как Baro - под этой линией. Хорошо видно, что получился почти что "выстрел наугад". Возможности одномерного ветвления CART не ограничены вычислением единственной линейной комбинации широты и долготы, и этот метод находит "критические значения" переменной Longitude , позволяющие получить наилучшую возможную (а в данном случае - идеальную) классификацию для переменной Class.

Рассмотрим теперь ситуацию, в которой проявляются слабые стороны деревьев классификации. Рассмотрим другой набор данных о циклонах. Их можно найти в демонстрационном файле данных Barotro2.sta.

Таблица 3
Таблица 3

ДАННЫЕ: Barotro2.sta 3v LONGITUD LATITUDE CLASS

59.00 59.50 60.00 60.50 61.00 61.00 61.50 61.50 62.00 63.00 63.50 64.00 64.50 65.00 65.00 65.00 65.50 65.50 65.50 66.00 66.00 66.00 66.50 66.50 66.50 67.00 67.50 68.00 68.50 69.00 69.00 69.50 69.50 70.00 70.50 71.00 71.50	17.00 21.00 12.00 16.00 13.00 15.00 17.00 19.00 14.00 15.00 19.00 12.00 16.00 12.00 15.00 17.00 16.00 19.00 21.00 13.00 14.00 17.00 17.00 18.00 21.00 14.00 18.00 14.00 18.00 13.00 15.00 17.00 19.00 12.00 16.00 17.00 21.00	BARO BARO TROP BARO TROP TROP BARO BARO TROP TROP BARO TROP TROP TROP TROP BARO TROP BARO BARO TROP TROP BARO BARO BARO BARO TROP BARO TROP BARO TROP TROP TROP BARO TROP TROP TROP BARO

Линейный дискриминантный анализ для переменной Класс - Class (Baro или Trop) с переменными Долгота - Longitude и Широта - Latitude в качестве предикторов правильно классифицирует все 37 наблюдений.


Анализ посредством дерева классификации по переменной Класс - Class в случае Полного перебора деревьев с одномерным ветвлением по методу CART также дает правильную классификацию для всех 37 циклонов, но для этого требуется дерево с 5 ветвлениями и 6 терминальными вершинами. Какой результат проще интерпретировать? В линейном дискриминантном анализе коэффициенты канонической дискриминантной функции при переменных Долгота - Longitude и Широта - Latitude равны соответственно 0.122073 и -0.633124, так что чем больше долгота и чем меньше широта, тем вероятнее данный циклон будет классифицирован как Trop. Интерпретация может быть такой: циклоны в южных широтах западной Атлантики вероятнее всего будут циклонами Trop, а циклоны в северных широтах восточной Атлантики - Baro.

Ниже показан Граф дерева для дерева классификации в варианте анализа, в котором используется Полный перебор деревьев с одномерным ветвлением по методу CART.



Можно было бы последовательно описать все ветвления дерева классификации, как это было проделано в предыдущем примере, но поскольку ветвлений много, интерпретировать результаты было бы труднее, чем в случае одной дискриминантной функции, получающейся при линейном дискриминантном анализе.
Вспомним, однако, про опцию Многомерное ветвление по линейным комбинациям порядковых предикторов, о которой мы говорили в разделе, посвященном гибким возможностям модуля Деревья классификации, и которая использует алгоритмы QUEST. Граф дерева для дерева классификации , построенного путем ветвления по линейным комбинациям, показан ниже.



Обратите внимание на то, что уже одно ветвление дерева дает идеальный прогноз. Каждая из терминальных вершин - "чистая", то есть не содержит наблюдений неправильно классифицированных циклонов. Ветвление по линейной комбинации в корневой вершине, ведущее к левой дочерней вершине и правой дочерней вершине, имеет вид "F(0) -.2342". Это означает, что если значение функции ветвления (обозначено через F(0) ) для данного циклона меньше или равно -0.2342 , то он попадет в левую дочернюю вершину и будет классифицирован как Baro, в противном случае он попадет в правую дочернюю вершину и будет классифицирован как Trop.


Коэффициенты функции ветвления (0.011741 для Долготы и -0. 060896 для Широты) имеют одинаковый знак и по относительной величине близки к соответствующим коэффициентам линейной дискриминантной функции из линейного дискриминантного анализа, так что оба метода в этом примере с прогнозированием переменной Class являются функционально эквивалентными.

Мораль всей этой истории об успехах и неудачах метода деревьев классификации можно сформулировать так: метод деревьев классификации хорош настолько, насколько удачным окажется выбор варианта анализа. Чтобы построить модель, дающую хороший прогноз, в любом случае нужно хорошо понимать природу взаимосвязей между предикторными и зависимыми переменными.
Итак, мы увидели, что методы анализа с помощью деревьев классификации можно охарактеризовать как набор иерархических, чрезвычайно гибких средств предсказания принадлежности наблюдений (объектов) к определенному классу значений категориальной зависимой переменной по значениям одной или нескольких предикторных переменных. Теперь мы готовы к тому, чтобы рассмотреть методы построения деревьев классификации более детально.

Информацию о том, для чего нужны деревья классификации, см. в разделе Основные идеи. См. также раздел Методы разведочного анализа данных.

В начало

Вычислительные методы

Процесс построения дерева классификации состоит из четырех основных шагов: Выбор критерия точности прогноза Выбор типа ветвления Определение момента прекращения ветвлений Определение "подходящих" размеров дерева
 

Выбор критерия точности прогноза
Выбор критерия точности прогноза

В конечном счете, цель анализа с помощью деревьев классификации состоит в том, чтобы получить максимально точный прогноз. К сожалению, очень сложно четко сформулировать, что такое точный прогноз. Эта проблема решается "переворачиванием с ног на голову": наиболее точным прогнозом считается такой, который связан с наименьшей ценой. Термин цена не содержит в себе ничего загадочного.


В большинстве приложений цена - это просто доля неправильно классифицированных наблюдений. Понятие цена вводится для того, чтобы распространить на более широкий класс ситуаций ту идею, что самый лучший прогноз - такой, который дает наименьший процент неправильных классификаций.

Необходимость минимизировать не просто долю неправильно классифицированных наблюдений, а именно потери, возникает тогда, когда некоторые ошибки прогноза ведут к более катастрофическим последствиям, чем другие, или же когда ошибки некоторого типа встречаются чаще других. Цена ошибки классификации для игрока, поставившего все свое состояние на одну ставку, несоизмеримо больше, чем от проигрыша нескольких ставок, на которые были поставлены мелкие суммы. Может случиться и наоборот, что потери от проигрыша большого количества мелких ставок будут больше, чем от проигрыша небольшого числа крупных. Усилия, которые следует уделять для минимизации убытков от ошибок прогноза, должны быть тем больше, чем больше возможный размер этих убытков.

Априорные вероятности.
Априорные вероятности.

Заметим, однако, что если Априорные вероятности выбраны пропорциональными размерам классов, а Цена ошибки классификации - одинаковая для всех классов, то минимизация потерь в точности эквивалентна минимизации доли неправильно классифицированных наблюдений. Рассмотрим априорные вероятности подробнее. Эти величины выражают то, как мы, не располагая никакой априорной информацией о значениях предикторных переменных модели, оцениваем вероятность попадания объекта в тот или иной класс. Например, изучая данные об учащихся, исключенных из школ, мы обнаружим, что в целом их количество существенно меньше, чем тех, кто продолжает учебу (т.е. различны исходные частоты); поэтому априорная вероятность того, что учащийся покинет школу, меньше, чем вероятность того, что он продолжит учебу.

Выбор априорных вероятностей, используемых для минимизации потерь, очень сильно влияет на результаты классификации. Если различия между исходными частотами в данной задаче не считаются существенными или если мы знаем заранее, что классы содержат примерно одинаковое количество наблюдений, то тогда можно взять одинаковые априорные вероятности.


В случаях, когда исходные частоты связаны с размерами классов (так будет, например, когда мы работаем со случайной выборкой), следует в качестве оценок для априорных вероятностей взять относительные размеры классов в выборке. Наконец, если Вы (например, на основании данных предыдущих исследований) располагаете какой-то информацией об исходных частотах, то априорные вероятности нужно выбирать с учетом этой информации. Например, априорная вероятность человека быть носителем рецессивного гена вдвое выше вероятности того, что этот ген имеет проявления. В любом случае, приписывая классу ту или иную априорную вероятность, мы "учитываем" степень важности ошибки классификации объектов этого класса. Минимизация потерь - это минимизация общего числа неправильно классифицированных наблюдений с Априорными вероятностями, пропорциональными размерам классов (и Ценами ошибки классификации, одинаковыми для всех классов), поскольку прогноз, чтобы давать меньший итоговый процент ошибок классификации, должен быть более точным на больших классах.

Цена ошибки классификации.
Цена ошибки классификации.

Бывает так, что по причинам, не связанным с размерами классов, для одних классов требуется более точный прогноз, чем для других. Гораздо важнее выявить переносчиков инфекционного заболевания, постоянно контактирующих с другими людьми, чем тех же переносчиков, не имеющих постоянных контактов, - и это независимо от относительной численности тех и других. Если мы примем, что избежать контактов с "контактирующим переносчиком" гораздо важнее, чем с "неконтактирующим", то следует приписать ошибочной классификации "контактирующего" как "неконтактирующего" большую цену, чем ошибочной классификации "неконтактирующего" как "контактирующего". Как уже говорилось, минимизация потерь - это минимизация общей доли неправильно классифицированных наблюдений с Априорными вероятностями, пропорциональными размерам классов, и Ценами ошибки классификации, одинаковыми для всех классов.


Веса наблюдений.
Веса наблюдений.

На менее концептуальном уровне, использование весов для весовой переменной в качестве множителей наблюдений для агрегированных данных также имеет отношение к минимизации потерь. Любопытно, что вместо того, чтобы использовать веса наблюдений для агрегированных данных, можно ввести подходящие априорные вероятности и/или цены ошибки классификации и получить те же самые результаты, не тратя времени на обработку множества наблюдений, имеющих одинаковые значения всех переменных. Предположим, например, что в агрегированном множестве данных с двумя равновеликими классами веса наблюдений из первого класса равны 2, а наблюдений из второго класса - 3. Если положить априорные вероятности равными соответственно 0.4 и 0.6, цены ошибки классификации взять одинаковыми и проанализировать данные без весов наблюдений, то доля неправильных классификаций получится такой же, как если бы мы оценили априорные вероятности по размерам классов, цены ошибки классификации взяли бы одинаковыми и анализировали агрегированные данные с использованием весов наблюдений. Точно такая же доля ошибок классификации получилась бы и в том случае, если бы мы положили все априорные вероятности одинаковыми, цену ошибочной классификации объекта из 1-го класса как принадлежащего ко 2-му классу взяли равной 2/3 от цены неправильной классификации объекта 2-го класса как принадлежащего 1-му классу, и анализировали бы данные без весов наблюдений.

За исключением простейших случаев, взаимосвязи между априорными вероятностями, ценами ошибок классификации и весами наблюдений являются довольно сложными (см. Breiman и др., 1984; Ripley, 1996). Однако если минимизация цены соответствует минимизации доли неправильных классификаций, все эти обстоятельства можно не принимать во внимание. Априорные вероятности, цена ошибок классификации и веса наблюдений были рассмотрены здесь для того, чтобы показать, как самые разнообразные ситуации в прогнозировании можно охватить единой концепцией минимизации цены, - в противоположность достаточно узкому (хотя, возможно, часто встречающемуся) классу задач прогнозирования, для которых подходит более ограниченная (хотя и простая) идея минимизации доли неправильных классификаций.


Далее, минимизация цены есть истинная цель классификации посредством деревьев классификации, и это отчетливо проявляется на четвертом (заключительном) этапе анализа: стремясь выбрать дерево "нужного размера", мы в действительности выбираем дерево с минимальной оценкой для цены. Для многих видов задач прогнозирования понять смысл уменьшения оценки для цены бывает очень важно для лучшего понимания окончательных результатов всего анализа.

Выбор типа ветвления
Выбор типа ветвления

Второй шаг анализа с помощью деревьев классификации заключается в том, чтобы выбрать способ ветвления по значениям предикторных переменных, которые используются для предсказания принадлежности анализируемых объектов к определенным классам значений зависимой переменной. В соответствии с иерархической природой деревьев классификации, такие ветвления производятся последовательно, начиная с корневой вершины, переходя к вершинам-потомкам, пока дальнейшее ветвление не прекратится и "неразветвленные" вершины-потомки окажутся терминальными. Ниже описаны три метода типа ветвления.

Дискриминантное одномерное ветвление.
Дискриминантное одномерное ветвление.

Если выбрано Одномерное ветвление, прежде всего нужно решить вопрос, какую из терминальных вершин дерева, построенного к данному моменту, следует расщепить на данном шаге и какую из предикторных переменных при этом использовать. Для каждой терминальной вершины вычисляются p-уровни для проверки значимости зависимостей между принадлежностью объектов к классам и уровнями каждой из предикторных переменных. В случае категориальных предикторов p-уровни вычисляются для проверки критерия Хи-квадрат для гипотезы независимости принадлежности классам от уровня категориального предиктора в данном узле дерева. В случае порядковых предикторов p-уровни вычисляются для анализа ANOVA взаимосвязи классовой принадлежности и значений порядкового предиктора в данном узле. Если наименьший из вычисленных p-уровней оказался меньше p-уровня Бонферони для множественных 0.05-сравнений, принимаемого по умолчанию, или иного порогового значения, установленного пользователем, то для разветвления этого узла выбирается та предикторная переменная, которая и дала этот наименьший.


Если среди p- уровней не оказалось ни одного, меньшего чем заданное пороговое значение, то p-уровни вычисляются по статистическим критериям, устойчивым к виду распределения, например F Левена. Более подробно процедура выбора узла и предикторной переменной для ветвления в случае, когда ни один из p-уровней не опустился ниже заданного порога, описана в Loh и Shih (1997).

Следующий шаг - собственно ветвление. В случае порядковых предикторов для построения двух относящихся к данной вершине "суперклассов" применяется алгоритм кластеризации 2-средних, описанный в Hartigan , Wong (1979, см. также Кластерный анализ). При этом находятся корни квадратного уравнения, характеризующего различие средних значений по "суперклассам" порядкового предиктора, и для каждого из корней вычисляются значения порога ветвления. Выбирается вариант ветвления, для которого значение ближе к среднему по "суперклассу". В случае категориального предиктора создаются фиктивные переменные, представляющие уровни этого предиктора, а затем с помощью метода сингулярного разложения фиктивные переменные преобразуются в совокупность неизбыточных порядковых предикторов. Затем применяется описанный выше алгоритм для порядковых предикторов, после чего полученное ветвление "проецируется обратно" в уровни исходной категоризующей переменной и трактуется как различие между двумя множествами уровней этой переменной. Как и в предыдущем случае, за подробностями мы отсылаем читателя к книге Loh , Shih (1997). Описанные процедуры довольно сложны, однако они позволяют уменьшить смещение при выборе ветвления, которое характерно для Полного перебора деревьев с одномерным ветвлением по методу CART. Смещение имеет место в сторону выбора переменных с большим числом уровней ветвления, и при интерпретации результатов оно может исказить относительную значимость влияния предикторов на значения зависимой переменной (см. Breiman и др., 1984).

Дискриминантное многомерное ветвление по линейным комбинациям.


Дискриминантное многомерное ветвление по линейным комбинациям.

Другим типом ветвления является многомерное ветвление по линейным комбинациям для порядковых предикторных переменных (при этом требуется, чтобы предикторы были измерены как минимум по интервальной шкале). Любопытно, что в этом методе способ использования непрерывных предикторных переменных, участвующих в линейной комбинации, очень похож на тот, который применялся в предыдущем методе для категоризующих переменных. С помощью сингулярного разложения непрерывные предикторы преобразуются в новый набор неизбыточных предикторов. Затем применяются процедуры создания "суперклассов" и поиска ветвления, ближайшего к среднему по "суперклассу", после чего результаты "проецируются назад" в исходные непрерывные предикторы и представляются как одномерное ветвление линейной комбинации предикторных переменных.

Полный перебор деревьев с одномерным ветвлением по методу CART.
Полный перебор деревьев с одномерным ветвлением по методу CART.

Третий метод выбора варианта ветвления, реализованный в данном модуле - Полный перебор деревьев с одномерным ветвлением по методу CART для категоризующих и порядковых предикторных переменных. В этом методе перебираются все возможные варианты ветвления по каждой предикторной переменной, и находится тот из них, который дает наибольший рост для критерия согласия (или, что то же самое, наибольшее уменьшение отсутствия согласия). Что определяет набор возможных ветвлений в некотором узле? Для категоризующей предикторной переменной, принимающей в данном узле k значений, имеется ровно 2(k-1) - 1 вариантов разбиения множества ее значений на две части. Для порядкового предиктора, имеющего в данном узле k различных уровней, имеется k -1 точек, разделяющих разные уровни. Мы видим, что количество различных вариантов ветвления, которые необходимо просмотреть, будет очень большим, если в задаче много предикторов, у них много уровней значений и в дереве много терминальных вершин. Каким образом определяется улучшение критерия согласия? В модуле Деревья классификации доступны три способа измерения критерия согласия.


Мера Джини однородности вершины принимает нулевое значение, когда в данной вершине имеется всего один класс (если используются априорные вероятности, оцененные по размерам классов или исходя из одинаковой цены ошибок классификации, то мера Джини вычисляется как сумма всех попарных произведений относительных размеров классов, представленных в данной вершине; ее значение будет максимальным, когда размеры всех классов одинаковы). Меру Джини в качестве критерия согласия использовали разработчики пакета CART (Breiman и. др., 1984). В модуле Деревья классификации имеются еще две возможности: мера Хи-квадрат Бартлетта (Bartlett, 1948) и мера G-квадрат measure, совпадающая с мерой максимума правдоподобия Хи-квадрат, которая применяется в моделировании структурными уравнениями (см., например, документацию по модулю Моделирование структурными уравнениями). При Полном переборе деревьев с одномерным ветвлением по методу CART ищется вариант ветвления, при котором максимально уменьшается значение выбранного критерия согласия. Классификация будет абсолютно точной, если согласие окажется полным.

Определение момента прекращения ветвлений
Определение момента прекращения ветвлений

Третий этап анализа с помощью деревьев классификации заключается в выборе момента, когда следует прекратить дальнейшие ветвления. Деревья классификации обладают тем свойством, что если не установлено ограничение на число ветвлений, то можно прийти к "чистой" классификации, когда каждая терминальная вершина содержит только один класс наблюдений (объектов). Однако обычно такая "чистая" классификация нереальна. Даже в простом дереве классификации из примера с сортировкой монет будут происходить ошибки классификации из-за того, что некоторые монеты имеют неправильный размер и/или размеры прорезей для них меняются со временем от износа. В принципе, такие ошибки можно было бы устранить, подвергая дальнейшей классификации монеты, провалившиеся в каждую прорезь, однако на практике всегда приходится в какой-то момент прекращать сортировку и удовлетворяться полученными к этому времени результатами.



Аналогично, если при анализе с помощью дерева классификации данные о классификации зависимой переменной или уровни значений предикторных переменных содержат ошибки измерений или составляющую шума, то было бы нереально пытаться продолжать сортировку до тех пор, пока каждая терминальная вершина не станет "чистой". В модуле Деревья классификации имеются две опции для управления остановкой ветвлений. Их выбор прямо связан с выбором для данной задачи Правила остановки.

Число неклассифицированных.
Число неклассифицированных.

В этом варианте ветвления продолжаются до тех пор, пока все терминальные вершины не окажутся чистыми или будут содержать не более чем заданное число объектов (наблюдений). Эта опция доступна в качестве Правила остановки в двух вариантах: По ошибке классификации или По вариации. Нужное минимальное число наблюдений задается как Число неклассифицированных, и ветвление прекращается, когда все терминальные вершины, содержащие более одного класса, содержат не более чем заданное число объектов (наблюдений).

Доля неклассифицированных.
Доля неклассифицированных.

При выборе этого варианта ветвления продолжаются до тех пор, пока все терминальные вершины не окажутся чистыми или будут содержать количество объектов, не превышающее заданную долю численности одного или нескольких классов. Требуемую минимальную долю следует задать как Долю неклассифицированных и тогда, если априорные вероятности взяты одинаковыми и размеры классов также одинаковы, ветвление прекратится, когда все терминальные вершины, содержащие более одного класса, будут содержать количество наблюдений, не превышающее заданную долю объема одного или нескольких классов. Если же априорные вероятности выбирались не одинаковыми, то ветвление прекратится, когда все терминальные вершины, содержащие более одного класса, будут содержать количество наблюдений, не превышающее заданную долю объема одного или нескольких классов.

Определение "подходящих" размеров дерева
Определение "подходящих" размеров дерева



Некий дотошный любитель играть на скачках, тщательно изучив все результаты очередного дня, конструирует огромное дерево классификации с множеством ветвлений, полностью учитывающее все данные по каждой лошади и каждому заезду. Предвкушая финансовый успех, он берет точную копию своего Графа дерева, с помощью дерева классификации сортирует лошадей, участвующих в заездах на следующий день, строит свой прогноз, делает ставки в соответствии с ним и ... уходит с ипподрома несколько менее богатым человеком, чем рассчитывал. Наш игрок наивно полагал, что дерево классификации, построенное по обучающей выборке с заранее известными результатами будет так же хорошо предсказывать результат и для другой - независимой тестовой выборки. Его дерево классификации не выдержало кросс-проверки. Вполне вероятно, что денежный выигрыш нашего игрока был бы гораздо значительнее, если бы он использовал небольшое дерево классификации , не вполне идеально классифицирующее обучающую выборку, но обладающее способностью столь же хорошо прогнозировать результат для тестовой выборки.

Можно высказать ряд общих соображений о том, что следует считать "подходящими размерами" для дерева классификации. Оно должно быть достаточно сложным для того, чтобы учитывать имеющуюся информацию, и в то же время оно должно быть как можно более простым. Дерево должно уметь использовать ту информацию, которая улучшает точность прогноза, и игнорировать ту информацию, которая прогноза не улучшает. По возможности оно должно углублять наше понимание того явления, которое мы пытаемся описать посредством этого дерева. Очевидно, однако, что сказанное можно отнести вообще к любой научной теории, так что мы должны более конкретно определить, что же такое дерево классификации "подходящего размера". Одна из возможных стратегий состоит в том, чтобы наращивать дерево до нужного размера, каковой определяется самим пользователем на основе уже имеющихся данных, диагностических сообщений системы, выданных на предыдущих этапах анализа, или, на крайний случай, интуиции.


Другая стратегия связана с использованием хорошо структурированного и документированного набора процедур для выбора "подходящего размера" дерева, разработанных Бриманом (Breiman) и др. (1984). Нельзя сказать (и авторы это явно отмечают), чтобы эти процедуры были доступны новичку, но они позволяют получить из процесса поиска дерева "подходящего размера" некоторые субъективные суждения.

Прямая остановка по методу FACT.
Прямая остановка по методу FACT.

Начнем с описания первой стратегии, в которой пользователь сам устанавливает размеры дерева классификации, до которых оно может расти. В этом варианте мы в качестве Правила остановки выбираем опцию Прямая остановка по методу FACT, а затем задаем Долю неклассифицированных, которая позволяет дереву расти до нужного размера. Ниже описаны три возможных способа определения, удачно ли выбран размер дерева, три варианта кросс-проверки для построенного дерева классификации.

Кросс-проверка на тестовой выборке.
Кросс-проверка на тестовой выборке.

Первый, наиболее предпочтительный вариант кросс-проверки - кросс-проверка на тестовой выборке. В этом варианте кросс-проверки дерево классификации строится по обучающей выборке, а его способность к прогнозированию проверяется путем предсказания классовой принадлежности элементов тестовой выборки. Если значение цены на тестовой выборке окажется больше, чем на обучающей выборке (напомним Вам, что цена - это доля неправильно классифицированных наблюдений при условии, что были использованы оцениваемые априорные вероятности, а цены ошибок классификации были взяты одинаковыми), то это свидетельствует о плохом результате кросс-проверки, и, возможно, в этом случае следует поискать дерево другого размера, которое бы лучше выдерживало кросс-проверку. Тестовая и обучающая выборки могут быть образованы из двух независимых наборов данных, или, если в нашем распоряжении имеется большая обучающая выборка, мы можем случайным образом отобрать часть (например, треть или половину) наблюдений и использовать ее в качестве тестовой выборки.



V-кратная кросс-проверка.
V-кратная кросс-проверка.

Второй тип кросс-проверки, реализованный в модуле Деревья классификации, - так называемая V-кратная кросс-проверка. Этот вид кросс-проверки разумно использовать в случаях, когда в нашем распоряжении нет отдельной тестовой выборки, а обучающее множество слишком мало для того, чтобы из него выделять тестовую выборку. Задаваемое пользователем значение V (значение по умолчанию равно 3) определяет число случайных подвыборок - по возможности одинакового объема, - которые формируются из обучающей выборки. Дерево классификации нужного размера строится V раз, причем каждый раз поочередно одна из подвыборок не используется в его построении, но затем используется как тестовая выборка для кросс-проверки. Таким образом, каждая подвыборка V - 1 раз участвует в обучающей выборке и ровно один раз служит тестовой выборкой. Цены кросс-проверки, вычисленные для всех V тестовых выборок, затем усредняются, и в результате получается V-кратная оценка для цены кросс-проверки, которая, вместе со своей стандартной ошибкой, доступна в таблице результатов Последовательность деревьев.

Глобальная кросс-проверка.
Глобальная кросс-проверка.

Третий тип кросс-проверки, реализованный в модуле Деревья классификации - глобальная кросс-проверка. В этом варианте производится заданное число итераций (по умолчанию - 3), причем всякий раз часть обучающей выборки (равная единице, деленной на заданное целое число) оставляется в стороне, а затем по очереди каждая из отложенных частей используется как тестовая выборка для кросс-проверки построенного дерева классификации. Этот вариант кросс-проверки, вероятно, уступает методу V-кратной кросс-проверки в случае, если была выбрана опция Прямая остановка по методу FACT, однако он может оказаться очень полезным для проверки методов автоматического построения дерева (обсуждение этих вопросов см. в Breiman и др., 1984). В результате мы естественно приходим ко второй из возможных стратегий выбора "подходящего размера" для дерева - методу автоматического построения дерева, который основывается на результатах Breiman и др. (1984) и называется "кросс-проверочным отсечением по минимальной цене-сложности".



Кросс-проверочное отсечение по минимальной цене-сложности.
Кросс-проверочное отсечение по минимальной цене-сложности.

Для того чтобы в Деревья классификации выполнить кросс-проверочное отсечение по минимальной цене-сложности, нужно выбрать опцию По ошибке классификации в качестве Правила остановки, а кросс-проверочное отсечение по минимальному отклонению-сложности выполняется, если в качестве Правила остановки выбрано отсечение По вариации. Единственное различие между этими двумя опциями - способ измерения ошибки прогноза. При отсечении По ошибке классификации используется неоднократно упоминавшаяся функция потерь (равная доли неправильно классифицированных объектов при оцениваемых априорных вероятностях и одинаковых ценах ошибок классификации). При отсечении По вариации используется мера, основанная на принципе максимума правдоподобия и называемая отклонением (см. Ripley, 1996). Мы сосредоточимся на кросс-проверочном отсечении по минимальной цене-сложности (предложенном Breiman и др., 1984), поскольку отсечение по отклонению-сложности отличается от него только способом измерения ошибки прогноза.

Функция цены, которая требуется для кросс-проверочного отсечения по минимальной цене-сложности, вычисляется по мере построения дерева, начиная с ветвления в корневой вершине, пока дерево не достигнет максимально допустимого размера, определяемого величиной Число неклассифицированных. Цена для обучающей выборки пересчитывается при каждом новом ветвлении дерева, так что в результате получается, вообще говоря, убывающая последовательность цен (это отражает улучшение качества классификации). Цена обучающей выборки называется ценой обучения, чтобы отличать ее от цены кросс-проверки, - это необходимо делать, поскольку V-кратная кросс-проверка также производится при каждом новом ветвлении дерева. В качестве значения цены для корневой вершины следует использовать оценку цены кросс-проверки из V-кратной кросс-проверки. Размер дерева можно определить как число терминальных вершин, потому что для бинарных деревьев при каждом новом ветвлении размер дерева увеличивается на единицу.


Введем теперь так называемый параметр сложности. Положим его сначала равным нулю, и для каждого дерева (начиная с исходного, состоящего из одной вершины) будем вычислять функцию, равную цене дерева плюс значение параметра сложности, умноженное на размер дерева. Станем теперь постепенно увеличивать значение параметра сложности, пока значение этой функции для максимального дерева не превысит ее значения для какого-либо из деревьев меньшего размера, построенных на предыдущих шагах. Примем это меньшее дерево за новое максимальное дерево и будем дальше увеличивать значение параметра сложности, пока значение функции для этого дерева не станет больше ее значения для какого-то еще меньшего дерева. Будем продолжать этот процесс до тех пор, пока дерево, состоящее из единственной корневой вершины, не станет максимальным. (Читатели, знакомые с численными методами, заметили, что в этом алгоритме мы использовали так называемую штрафную функцию. Она представляет собой линейную комбинацию цены, которая в общем случае убывает с ростом дерева, и размера дерева, который линейно растет. По мере того, как значение параметра сложности увеличивается, большие по размеру деревья получают все больший штраф за свою сложность, пока не будет достигнуто пороговое значение, при котором более высокая цена меньшего дерева будет перевешиваться сложностью большего дерева.

Последовательность максимальных деревьев, которая получается в процессе выполнения этого алгоритма, обладает рядом замечательных свойств. Они являются вложенными, поскольку при последовательном усечении каждое дерево содержит все вершины следующего (меньшего) дерева в последовательности. Поначалу при переходе от очередного дерева к последующему отсекается, как правило, большое число вершин, однако по мере приближения к корневой вершине на каждом шаге будет отсекаться все меньше вершин. Деревья последовательности усекаются оптимально в том смысле, что каждое дерево в последовательности имеет наименьшую цену среди всех деревьев такого же размера.


Доказательства и подробные пояснения можно найти в Breiman и др. (1984).

Выбор дерева по результатам усечений.
Выбор дерева по результатам усечений.

Выберем теперь из последовательности оптимально усеченных деревьев дерево "подходящего размера". Естественным критерием здесь является Цена кросс-проверки. Не будет никакой ошибки, если мы в качестве дерева "подходящего размера" выберем то, которое дает наименьшую цену кросс-проверки, однако часто оказывается, что есть еще несколько деревьев с ценой кросс-проверки, близкой к минимальной. Breiman и др. (1984) высказывают разумное предложение, что в качестве дерева "подходящего размера" нужно брать наименьшее (наименее сложное) из тех, чьи цены кросс-проверки несущественно отличаются от минимальной. Авторы предложили правило "1 SE": в качестве дерева "подходящего размера" нужно брать наименьшее дерево из тех, чьи цены кросс-проверки не превосходят минимальной цены кросс-проверки плюс умноженная на единицу стандартная ошибка цены кросс-проверки для дерева с минимальной Ценой кросс-проверки.

Существенное преимущество "автоматического" выбора дерева состоит в том, что оно позволяет избежать как "недо-", так и "пересогласованности" с данными. На следующем рисунке изображены типичные графики цены обучения и цены кросс-проверки для цепочки последовательно усекаемых деревьев.



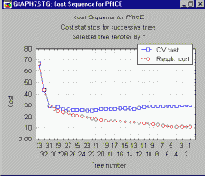
Как видно из графика, цена обучения (например, доля неправильных классификаций в обучающей выборке) заметно уменьшается с увеличением размера дерева. В то же время, цена кросс-проверки с ростом размера дерева быстро достигает минимума, а затем - для очень больших размеров дерева - начинает расти. Обратите внимание на то, что выбранное дерево "подходящего размера" располагается близко к точке перегиба этой кривой, то есть близко к той точке, где первоначальное резкое уменьшение цены кросс-проверки начинает сходить на нет. Процедура "автоматического" выбора дерева направлена на то, чтобы выбирать наиболее простое (наименьшее по размеру) дерево с ценой кросс-проверки, близкой к минимальной, и тем самым избегать потери точности прогноза, происходящей от "недо-" или " пересогласованности " с данными (похожая логика используется в графике каменистой осыпи для определения числа факторов в факторном анализе, см.


также Просмотр результатов анализа главных компонент)

Итак, мы видим, что кросс-проверочное отсечение по минимальной цене-сложности и последующий выбор дерева "подходящего размера" - действительно "автоматические" процедуры. Алгоритм самостоятельно принимает все решения, необходимые для выбора дерева "подходящего размера", за исключением разве что выбора множителя в SE-правиле. В связи с этим возникает вопрос о том, насколько хорошо воспроизводятся результаты, то есть, не может ли получиться так, что при повторении этого процесса "автоматического выбора" будут строиться деревья, сильно отличающиеся друг от друга по размеру. Именно здесь очень полезной может оказаться глобальная кросс-проверка. Как уже говорилось выше, при глобальной кросс-проверке все этапы анализа повторяются заданное число раз (по умолчанию - 3), и при этом часть наблюдений используется как тестовая выборка для кросс-проверки полученного дерева классификации. Если средняя цена тестовых выборок, которая называется ценой глобальной кросс-проверки, превышает цену кросс-проверки выбранного дерева, или если стандартная ошибка цены глобальной кросс-проверки превышает стандартную ошибку цены кросс-проверки для выбранного дерева, то это свидетельствует о том, что процедура "автоматического" выбора дерева вместо устойчивого выбора дерева с минимальным оцененным значением цены дает недопустимо большой разброс результатов.

Деревья классификации в сравнении с традиционными методами.
Деревья классификации в сравнении с традиционными методами.

Как видно из описания методов построения деревьев классификации, в целом ряде аспектов метод деревьев классификации существенно отличается от традиционных статистических методов предсказания принадлежности объекта к определенному классу значений категориальной зависимой переменной. Для сортировки объектов по классам здесь применяется иерархия (последовательность) прогнозов, при этом для одного и того же объекта прогноз может делаться много раз.


В отличие от этого, в традиционных методах используется техника, при которой отнесение каждого объекта к тому или иному классу производится один раз и окончательно. В других отношениях, например по своей конечной цели - достижению точного прогноза, - анализ методом деревьев классификации не отличается от классических методов. Время покажет, достаточно ли у этого метода достоинств, чтобы встать в один ряд с традиционными методами.

Об основных целях анализа с помощью деревьев классификации см. раздел Основные идеи. Об иерархической природе и гибкости деревьев классификации см. раздел Характеристики деревьев классификации.
См. также Методы разведочного анализа данных.

В начало

Сравнение с другими пакетами, в которых реализован метод деревьев классификации

Для решения задачи прогнозирования принадлежности объекта (случая) к определенному классу значений зависимой категориальной переменной по данным измерений одной или нескольких предикторных переменных было разработано большое число программ, реализующих метод деревьев классификации. В предыдущем разделе Вычислительные методы мы рассмотрели методы программ QUEST (Loh & Shih, 1997) и CART (Breiman и др., 1984), предназначенные для построения бинарного дерева классификации с помощью одномерных ветвлений для категориальных, порядковых (т.е. измеренных как минимум в порядковой шкале) или смеси обоих типов предикторных переменных. Кроме того, в данном модуле имеется возможность строить дерево классификации с помощью ветвлений по линейным комбинациям для интервальных предикторных переменных.

Некоторые из программ деревьев классификации, в частности FACT (Loh & Vanichestakul, 1988) и THAID (Morgan & Messenger, 1973, сюда же относятся пакеты AID - Automatic Interaction Detection, Morgan & Sonquist, 1963, и CHAID - Chi-Square Automatic Interaction Detection, Kass, 1980) при построении дерева классификации выполняют не бинарные, а многоуровневые ветвления. При многоуровневом ветвлении от одной родительской вершины идут ветви в более чем две дочерние вершины, тогда как при бинарном (двоичном) ветвлении мы всегда получаем ровно две дочерние вершины (независимо от числа уровней переменной ветвления и числа классов зависимой переменной).


Необходимо отметить, что многоуровневое ветвление на самом деле не имеет никаких преимуществ (потому что любое многоуровневое ветвление может быть представлено в виде нескольких последовательных двоичных ветвлений), но может иметь определенные недостатки. В некоторых пакетах фиксированная предикторная переменная может быть использована для многоуровневого ветвления лишь один раз, так что получающееся в результате дерево классификации оказывается слишком коротким и неинтересным (Loh & Shih, 1997). Более серьезная трудность связана со смещением при выборе переменной для ветвления. Такое смещение возможно в любой программе типа THAID (Morgan & Sonquist, 1973), где применяется полный перебор вариантов ветвления (обсуждение этого вопроса см. в Loh & Shih, 1997). Смещение в выборе переменной проявляется в том, что преимущественно выбираются переменные, имеющие много уровней значений, и такое смещение может исказить относительную важность разных предикторных переменных в смысле их влияния на отклик зависимой переменной (см. Breiman и др., 1984).

Смещения в выборе переменной можно избежать, выбрав опцию дискриминантного одномерного или многомерного ветвления модуля Деревья классификации. При этом используются алгоритмы QUEST (Loh & Shih, 1997), предотвращающие смещение в выборе переменной. Опция Полный перебор деревьев с одномерным ветвлением по методу CART модуля Деревья классификации предназначена для тех ситуаций, когда целью анализа является отыскание системы ветвлений, дающей наилучшую классификацию обучающей выборки (которая необязательно окажется лучшей на независимом кросс-проверочной выборке). Для построения надежных вариантов ветвления, а также для большей скорости вычислений мы рекомендуем опцию дискриминантного одномерного ветвления. О построении дерева классификации см. в разделе Вычислительные методы.

Дополнительная информация по методам анализа данных, добычи данных, визуализации и прогнозированию содержится на Портале StatSoft (http://www.statsoft.ru/home/portal/default.asp) и в Углубленном Учебнике StatSoft (Учебник с формулами).


(c) Copyright StatSoft, Inc., 1984-2001
STATISTICA является торговой маркой StatSoft, Inc.

Дискриминантный анализ

Дискриминантный анализ

Основная цель Вычислительный подход Пошаговый дискриминантный анализ Интерпретация функции дискриминации для двух групп Дискриминантные функции для нескольких групп Предположения Классификация

Основная цель Вычислительный подход Пошаговый дискриминантный анализ Интерпретация функции дискриминации для двух групп Дискриминантные функции для нескольких групп Предположения Классификация

Основная цель
Основная цель

Дискриминантный анализ используется для принятия решения о том, какие переменные различают (дискриминируют) две или более возникающие совокупности (группы). Например, некий исследователь в области образования может захотеть исследовать, какие переменные относят выпускника средней школы к одной из трех категорий: (1) поступающий в колледж, (2) поступающий в профессиональную школу или (3) отказывающийся от дальнейшего образования или профессиональной подготовки. Для этой цели исследователь может собрать данные о различных переменных, связанных с учащимися школы. После выпуска большинство учащихся естественно должно попасть в одну из названных категорий. Затем можно использовать Дискриминантный анализ для определения того, какие переменные дают наилучшее предсказание выбора учащимися дальнейшего пути.

Медик может регистрировать различные переменные, относящиеся к состоянию больного, чтобы выяснить, какие переменные лучше предсказывают, что пациент, вероятно, выздоровел полностью (группа 1), частично (группа 2) или совсем не выздоровел (группа 3). Биолог может записать различные характеристики сходных типов (групп) цветов, чтобы затем провести анализ дискриминантной функции, наилучшим образом разделяющей типы или группы.

В начало

Вычислительный подход
Вычислительный подход

С вычислительной точки зрения дискриминантный анализ очень похож на дисперсионный анализ (см. раздел Дисперсионный анализ). Рассмотрим следующий простой пример. Предположим, что вы измеряете рост в случайной выборке из 50 мужчин и 50 женщин.
Женщины в среднем не так высоки, как мужчины, и эта разница должна найти отражение для каждой группы средних (для переменной Рост). Поэтому переменная Рост позволяет вам провести дискриминацию между мужчинами и женщинами лучше, чем, например, вероятность, выраженная следующими словами: "Если человек большой, то это, скорее всего, мужчина, а если маленький, то это вероятно женщина".

Вы можете обобщить все эти доводы на менее "тривиальные" группы и переменные. Например, предположим, что вы имеете две совокупности выпускников средней школы - тех, кто выбрал поступление в колледж, и тех, кто не собирается это делать. Вы можете собрать данные о намерениях учащихся продолжить образование в колледже за год до выпуска. Если средние для двух совокупностей (тех, кто в настоящее время собирается продолжить образование, и тех, кто отказывается) различны, то вы можете сказать, что намерение поступить в колледж, как это установлено за год до выпуска, позволяет разделить учащихся на тех, кто собирается и кто не собирается поступать в колледж (и эта информация может быть использована членами школьного совета для подходящего руководства соответствующими студентами).

В завершение заметим, что основная идея дискриминантного анализа заключается в том, чтобы определить, отличаются ли совокупности по среднему какой-либо переменной (или линейной комбинации переменных), и затем использовать эту переменную, чтобы предсказать для новых членов их принадлежность к той или иной группе.

Дисперсионный анализ.
Дисперсионный анализ.

Поставленная таким образом задача о дискриминантной функции может быть перефразирована как задача одновходового дисперсионного анализа (ANOVA). Можно спросить, в частности, являются ли две или более совокупности значимо отличающимися одна от другой по среднему значению какой-либо конкретной переменной. Для изучения вопроса о том, как можно проверить статистическую значимость отличия в среднем между различными совокупностями, вы можете прочесть раздел Дисперсионный анализ.


Однако должно быть ясно, что если среднее значение определенной переменной значимо различно для двух совокупностей, то вы можете сказать, что переменная разделяет данные совокупности.

В случае одной переменной окончательный критерий значимости того, разделяет переменная две совокупности или нет, дает F-критерий. Как описано в разделах Элементарные понятия статистики и Дисперсионный анализ, F статистика по существу вычисляется, как отношение межгрупповой дисперсии к объединенной внутригрупповой дисперсии. Если межгрупповая дисперсия оказывается существенно больше, тогда это должно означать различие между средними.

Многомерные переменные.
Многомерные переменные.

При применении дискриминантного анализа обычно имеются несколько переменных, и задача состоит в том, чтобы установить, какие из переменных вносят свой вклад в дискриминацию между совокупностями. В этом случае вы имеете матрицу общих дисперсий и ковариаций, а также матрицы внутригрупповых дисперсий и ковариаций. Вы можете сравнить эти две матрицы с помощью многомерного F-критерия для того, чтобы определить, имеются ли значимые различия между группами (с точки зрения всех переменных). Эта процедура идентична процедуре Многомерного дисперсионного анализа (MANOVA). Так же как в MANOVA, вначале можно выполнить многомерный критерий, и затем, в случае статистической значимости, посмотреть, какие из переменных имеют значимо различные средние для каждой из совокупностей. Поэтому, несмотря на то, что вычисления для нескольких переменных более сложны, применимо основное правило, заключающееся в том, что если вы производите дискриминацию между совокупностями, то должно быть заметно различие между средними.

В начало

Пошаговый дискриминантный анализ
Пошаговый дискриминантный анализ

Вероятно, наиболее общим применением дискриминантного анализа является включение в исследование многих переменных с целью определения тех из них, которые наилучшим образом разделяют совокупности между собой. Например, исследователь в области образования, интересующийся предсказанием выбора, который сделают выпускники средней школы относительно своего дальнейшего образования, произведет с целью получения наиболее точных прогнозов регистрацию возможно большего количества параметров обучающихся, например, мотивацию, академическую успеваемость и т.д.



Модель.
Модель.

Другими словами, вы хотите построить "модель", позволяющую лучше всего предсказать, к какой совокупности будет принадлежать тот или иной образец. В следующем рассуждении термин "в модели" будет использоваться для того, чтобы обозначать переменные, используемые в предсказании принадлежности к совокупности; о неиспользуемых для этого переменных будем говорить, что они "вне модели".

Пошаговый анализ с включением.
Пошаговый анализ с включением.

В пошаговом анализе дискриминантных функций модель дискриминации строится по шагам. Точнее, на каждом шаге просматриваются все переменные и находится та из них, которая вносит наибольший вклад в различие между совокупностями. Эта переменная должна быть включена в модель на данном шаге, и происходит переход к следующему шагу.

Пошаговый анализ с исключением.
Пошаговый анализ с исключением.

Можно также двигаться в обратном направлении, в этом случае все переменные будут сначала включены в модель, а затем на каждом шаге будут устраняться переменные, вносящие малый вклад в предсказания. Тогда в качестве результата успешного анализа можно сохранить только "важные" переменные в модели, то есть те переменные, чей вклад в дискриминацию больше остальных.

F для включения, F для исключения.
F для включения, F для исключения.

Эта пошаговая процедура "руководствуется" соответствующим значением F для включения и соответствующим значением F для исключения. Значение F статистики для переменной указывает на ее статистическую значимость при дискриминации между совокупностями, то есть, она является мерой вклада переменной в предсказание членства в совокупности. Если вы знакомы с пошаговой процедурой множественной регрессии, то вы можете интерпретировать значение F для включения/исключения в том же самом смысле, что и в пошаговой регрессии.

Расчет на случай.
Расчет на случай.

Пошаговый дискриминантный анализ основан на использовании статистического уровня значимости. Поэтому по своей природе пошаговые процедуры рассчитывают на случай, так как они "тщательно перебирают" переменные, которые должны быть включены в модель для получения максимальной дискриминации.


При использовании пошагового метода исследователь должен осознавать, что используемый при этом уровень значимости не отражает истинного значения альфа, то есть, вероятности ошибочного отклонения гипотезы H0 (нулевой гипотезы, заключающейся в том, что между совокупностями нет различия).

В начало

Интерпретация функции дискриминации для двух групп
Интерпретация функции дискриминации для двух групп

Для двух групп дискриминантный анализ может рассматриваться также как процедура множественной регрессии (и аналогичная ей) - (см. раздел Множественная регрессия; дискриминантный анализ для двух групп также называется Линейным дискриминантным анализом Фишера после работы Фишера (Fisher, 1936). (С вычислительной точки зрения все эти подходы аналогичны). Если вы кодируете две группы как 1 и 2, и затем используете эти переменные в качестве зависимых переменных в множественной регрессии, то получите результаты, аналогичные тем, которые получили бы с помощью Дискриминантного анализа. В общем, в случае двух совокупностей вы подгоняете линейное уравнение следующего типа:

Группа = a + b1*x1 + b2*x2 + ... + bm*xm

где a является константой, и b1...bm являются коэффициентами регрессии. Интерпретация результатов задачи с двумя совокупностями тесно следует логике применения множественной регрессии: переменные с наибольшими регрессионными коэффициентами вносят наибольший вклад в дискриминацию.

В начало

Дискриминантные функции для нескольких групп
Дискриминантные функции для нескольких групп

Если имеется более двух групп, то можно оценить более, чем одну дискриминантную функцию подобно тому, как это было сделано ранее. Например, когда имеются три совокупности, вы можете оценить: (1) - функцию для дискриминации между совокупностью 1 и совокупностями 2 и 3, взятыми вместе, и (2) - другую функцию для дискриминации между совокупностью 2 и совокупности 3. Например, вы можете иметь одну функцию, дискриминирующую между теми выпускниками средней школы, которые идут в колледж, против тех, кто этого не делает (но хочет получить работу или пойти в училище), и вторую функцию для дискриминации между теми выпускниками, которые хотят получить работу против тех, кто хочет пойти в училище.


Коэффициенты b в этих дискриминирующих функциях могут быть проинтерпретированы тем же способом, что и ранее.

Канонический анализ.
Канонический анализ.

Когда проводится дискриминантный анализ нескольких групп, вы не должны указывать, каким образом следует комбинировать группы для формирования различных дискриминирующих функций. Вместо этого, вы можете автоматически определить некоторые оптимальные комбинации переменных, так что первая функция проведет наилучшую дискриминацию между всеми группами, вторая функция будет второй наилучшей и т.д. Более того, функции будут независимыми или ортогональными, то есть их вклады в разделение совокупностей не будут перекрываться. С вычислительной точки зрения система вы проводите анализ канонических корреляций (см. также раздел Каноническая корреляция), которые будут определять последовательные канонические корни и функции. Максимальное число функций будет равно числу совокупностей минус один или числу переменных в анализе в зависимости от того, какое из этих чисел меньше.

Интерпретация дискриминантных функций.
Интерпретация дискриминантных функций.

Как было установлено ранее, вы получите коэффициенты b (и стандартизованные коэффициенты бета) для каждой переменной и для каждой дискриминантной (теперь называемой также и канонической) функции. Они могут быть также проинтерпретированы обычным образом: чем больше стандартизованный коэффициент, тем больше вклад соответствующей переменной в дискриминацию совокупностей. (Отметим также, что вы можете также проинтерпретировать структурные коэффициенты; см. ниже.) Однако эти коэффициенты не дают информации о том, между какими совокупностями дискриминируют соответствующие функции. Вы можете определить характер дискриминации для каждой дискриминантной (канонической) функции, взглянув на средние функций для всех совокупностей. Вы также можете посмотреть, как две функции дискриминируют между группами, построив значения, которые принимают обе дискриминантные функции (см., например, следующий график).





В этом примере Корень1 (root1), похоже, в основном дискриминирует между группой Setosa и объединением групп Virginic и Versicol. По вертикальной оси (Корень2) заметно небольшое смещение точек группы Versicol вниз относительно центральной линии (0).

Матрица факторной структуры.
Матрица факторной структуры.

Другим способом определения того, какие переменные "маркируют" или определяют отдельную дискриминантную функцию, является использование факторной структуры. Коэффициенты факторной структуры являются корреляциями между переменными в модели и дискриминирующей функцией. Если вы знакомы с факторным анализом (см. раздел Факторный анализ), то можете рассматривать эти корреляции как факторные нагрузки переменных на каждую дискриминантную функцию.

Некоторые авторы согласны с тем, что структурные коэффициенты могут быть использованы при интерпретации реального "смысла" дискриминирующей функции. Объяснения, даваемые этими авторами, заключаются в том, что: (1) - вероятно структура коэффициентов более устойчива и (2) - они позволяют интерпретировать факторы (дискриминирующие функции) таким же образом, как и в факторном анализе. Однако последующие исследования с использованием метода Монте-Карло (Барсиковский и Стивенс (Barcikowski, Stevens, 1975); Хьюберти (Huberty, 1975)) показали, что коэффициенты дискриминантных функций и структурные коэффициенты почти одинаково нестабильны, пока значение размер выборки не станет достаточно большим (например, если число наблюдений в 20 раз больше, чем число переменных). Важно помнить, что коэффициенты дискриминантной функции отражают уникальный (частный) вклад каждой переменной в отдельную дискриминантную функцию, в то время как структурные коэффициенты отражают простую корреляцию между переменными и функциями. Если дискриминирующей функции хотят придать отдельные "осмысленные" значения (родственные интерпретации факторов в факторном анализе), то следует использовать (интерпретировать) структурные коэффициенты.


Если же хотят определить вклад, который вносит каждая переменная в дискриминантную функцию, то используют коэффициенты (веса) дискриминантной функции.

Значимость дискриминантной функции.
Значимость дискриминантной функции.

Можно проверить число корней, которое добавляется значимо к дискриминации между совокупностями. Для интерпретации могут быть использованы только те из них, которые будут признаны статистически значимыми. Остальные функции (корни) должны быть проигнорированы.

Итог.
Итог.

Итак, при интерпретации дискриминантной функции для нескольких совокупностей и нескольких переменных, вначале хотят проверить значимость различных функций и в дальнейшем использовать только значимые функции. Затем, для каждой значащей функции вы должны рассмотреть для каждой переменной стандартизованные коэффициенты бета. Чем больше стандартизованный коэффициент бета, тем большим является относительный собственный вклад переменной в дискриминацию, выполняемую соответствующей дискриминантной функцией. В порядке получения отдельных "осмысленных" значений дискриминирующих функций можно также исследовать матрицу факторной структуры с корреляциями между переменными и дискриминирующей функцией. В заключение, вы должны посмотреть на средние для значимых дискриминирующих функций для того, чтобы определить, какие функции и между какими совокупностями проводят дискриминацию.

В начало

Предположения
Предположения

Как говорилось ранее, дискриминантный анализ в вычислительном смысле очень похож на многомерный дисперсионный анализ (MANOVA), и поэтому применимы все предположения для MANOVA, упомянутые в разделе Дисперсионный анализ. Фактически, вы можете использовать широкий набор диагностических правил и статистических критериев для проверки предположений, чтобы вы имели законные основания применения Дискриминантного анализа к вашим данным.

Нормальное распределение.
Нормальное распределение.

Предполагается, что анализируемые переменные представляют выборку из многомерного нормального распределения.


Поэтому вы можете проверить, являются ли переменные нормально распределенными. Отметим, однако, что пренебрежение условием нормальности обычно не является "фатальным" в том смысле, что результирующие критерии значимости все еще "заслуживают доверия". Вы также можете воспользоваться специальными критериями нормальности и графиками.

Однородность дисперсий/ковариаций.
Однородность дисперсий/ковариаций.

Предполагается, что матрицы дисперсий/ковариаций переменных однородны. Как и ранее, малые отклонения не фатальны, однако прежде чем сделать окончательные выводы при важных исследованиях, неплохо обратить внимание на внутригрупповые матрицы дисперсий и корреляций. В частности, можно построить матричную диаграмму рассеяния, весьма полезную для этой цели. При наличии сомнений попробуйте произвести анализ заново, исключив одну или две малоинтересных совокупности. Если общий результат (интерпретация) сохраняется, то вы, по-видимому, имеете разумное решение. Вы можете также использовать многочисленные критерии и способы для того, чтобы проверить, нарушено это предположение в ваших данных или нет. Однако, как упомянуто в разделе Дисперсионный анализ, многомерный M-критерий Бокса для проверки однородности матриц дисперсий/ковариаций, в частности, чувствителен к отклонению от многомерной нормальности и не должен восприниматься слишком "серьезно".

Корреляции между средними и дисперсиями.
Корреляции между средними и дисперсиями.

Большинство "реальных" угроз корректности применения критериев значимости возникает из-за возможной зависимости между средними по совокупностям и дисперсиями (или стандартными отклонениями) между собой. Интуитивно ясно, что если имеется большая изменчивость в совокупности с высокими средними в нескольких переменных, то эти высокие средние ненадежны. Однако критерии значимости основываются на объединенных дисперсиях, то есть, на средней дисперсии по всем совокупностям. Поэтому критерии значимости для относительно больших средних (с большими дисперсиями) будут основаны на относительно меньших объединенных дисперсиях и будут ошибочно указывать на статистическую значимость.


На практике этот вариант может произойти также, если одна из изучаемых совокупностей содержит несколько экстремальных выбросов, которые сильно влияют на средние и, таким образом, увеличивают изменчивость. Для определения такого случая следует изучить описательные статистики, то есть средние и стандартные отклонения или дисперсии для таких корреляций.

Задача с плохо обусловленной матрицей.
Задача с плохо обусловленной матрицей.

Другое предположение в дискриминантном анализе заключается в том, что переменные, используемые для дискриминации между совокупностями, не являются полностью избыточными. При вычислении результатов дискриминантного анализа происходит обращение матрицы дисперсий/ковариаций для переменных в модели. Если одна из переменных полностью избыточна по отношению к другим переменным, то такая матрица называется плохо обусловленной и не может быть обращена. Например, если переменная является суммой трех других переменных, то это отразится также и в модели, и рассматриваемая матрица будет плохо обусловленной.

Значения толерантности.
Значения толерантности.

Чтобы избежать плохой обусловленности матриц, необходимо постоянно проверять так называемые значения толерантности для каждой переменной. Значение толерантности вычисляется как 1 минус R-квадрат, где R-квадрат - коэффициент множественной корреляции для соответствующей переменной со всеми другими переменными в текущей модели. Таким образом, это есть доля дисперсии, относящаяся к соответствующей переменной. Вы можете также обратиться к разделу Множественная регрессия, чтобы узнать больше о методах множественной регрессии и об интерпретации значения толерантности. В общем случае, когда переменная почти полностью избыточна (и поэтому матрица задачи является плохо обусловленной), значение толерантности для этой переменной будет приближаться к нулю.

В начало

Классификация
Классификация

Другой главной целью применения дискриминантного анализа является проведение классификации. Как только модель установлена и получены дискриминирующие функции, возникает вопрос о том, как хорошо они могут предсказывать, к какой совокупности принадлежит конкретный образец?



Априорная и апостериорная классификация.
Априорная и апостериорная классификация.

Прежде чем приступить к изучению деталей различных процедур оценивания, важно уяснить, что эта разница ясна. Обычно, если вы оцениваете на основании некоторого множества данных дискриминирующую функцию, наилучшим образом разделяющую совокупности, и затем используете те же самые данные для оценивания того, какова точность вашей процедуры, то вы во многом полагаетесь на волю случая. В общем случае, получают, конечно худшую классификацию для образцов, не использованных для оценки дискриминантной функции. Другими словами, классификация действует лучшим образом для выборки, по которой была проведена оценка дискриминирующей функции (апостериорная классификация), чем для свежей выборки (априорная классификация). (Трудности с (априорной) классификацией будущих образцов заключается в том, что никто не знает, что может случиться. Намного легче классифицировать уже имеющиеся образцы.) Поэтому оценивание качества процедуры классификации никогда не производят по той же самой выборке, по которой была оценена дискриминирующая функция. Если желают использовать процедуру для классификации будущих образцов, то ее следует "испытать" (произвести кросс-проверку) на новых объектах.

Функции классификации.
Функции классификации.

Функции классификации не следует путать с дискриминирующими функциями. Функции классификации предназначены для определения того, к какой группе наиболее вероятно может быть отнесен каждый объект. Имеется столько же функций классификации, сколько групп. Каждая функция позволяет вам для каждого образца и для каждой совокупности вычислить веса классификации по формуле:

Si = ci + wi1*x1 + wi2*x2 + ... + wim*xm

В этой формуле индекс i обозначает соответствующую совокупность, а индексы 1, 2, ..., m обозначают m переменных; ci являются константами для i-ой совокупности, wij - веса для j-ой переменной при вычислении показателя классификации для i-ой совокупности; xj - наблюдаемое значение для соответствующего образца j-ой переменной.


Величина Si является результатом показателя классификации.

Поэтому вы можете использовать функции классификации для прямого вычисления показателя классификации для некоторых новых значений.

Классификация наблюдений.
Классификация наблюдений.

Как только вы вычислили показатели классификации для наблюдений, легко решить, как производить классификацию наблюдений. В общем случае наблюдение считается принадлежащим той совокупности, для которой получен наивысший показатель классификации (кроме случая, когда вероятности априорной классификации становятся слишком малыми; см. ниже). Поэтому, если вы изучаете выбор карьеры или образования учащимися средней школы после выпуска (поступление в колледж, в профессиональную школу или получение работы) на основе нескольких переменных, полученных за год до выпуска, то можете использовать функции классификации, чтобы предсказать, что наиболее вероятно будет делать каждый учащийся после выпуска. Однако вы хотели бы определить вероятность, с которой учащийся сделает предсказанный выбор. Эти вероятности называются апостериорными, и их также можно вычислить. Однако для понимания, как эти вероятности вычисляются, вначале рассмотрим так называемое расстояние Махаланобиса.

Расстояние Махаланобиса.
Расстояние Махаланобиса.

Вы можете прочитать об этих расстояниях в других разделах. В общем, расстояние Махаланобиса является мерой расстояния между двумя точками в пространстве, определяемым двумя или более коррелированными переменными. Например, если имеются всего две некоррелированных переменные, то вы можете нанести точки (образцы) на стандартную 2М диаграмму рассеяния. Расстояние Махаланобиса между точками будет в этом случае равно расстоянию Евклида, т.е. расстоянию, измеренному, например, рулеткой. Если имеются три некоррелированные переменные, то для определения расстояния вы можете по-прежнему использовать рулетку (на 3М диаграмме). При наличии более трех переменных вы не можете более представить расстояние на диаграмме. Также и в случае, когда переменные коррелированы, то оси на графике могут рассматриваться как неортогональные (они уже не направлены под прямыми углами друг к другу).


В этом случае простое определение расстояния Евклида не подходит, в то время как расстояние Махаланобиса является адекватно определенным в случае наличия корреляций.

Расстояние Махаланобиса и классификация.
Расстояние Махаланобиса и классификация.

Для каждой совокупности в выборке вы можете определить положение точки, представляющей средние для всех переменных в многомерном пространстве, определенном переменными рассматриваемой модели. Эти точки называются центроидами группы. Для каждого наблюдения вы можете затем вычислить его расстояние Махаланобиса от каждого центроида группы. Снова, вы признаете наблюдение принадлежащим к той группе, к которой он ближе, т.е. когда расстояние Махаланобиса до нее минимально.

Апостериорные вероятности классификации.
Апостериорные вероятности классификации.

Используя для классификации расстояние Махаланобиса, вы можете теперь получить вероятность того, что образец принадлежит к конкретной совокупности. Это значение будет не вполне точным, так как распределение вокруг среднего для каждой совокупности будет не в точности нормальным. Так как принадлежность каждого образца вычисляется по априорному знанию модельных переменных, эти вероятности называются апостериорными вероятностями. Короче, апостериорные вероятности - это вероятности, вычисленные с использованием знания значений других переменных для образцов из частной совокупности. Некоторые пакеты автоматически вычисляют эти вероятности для всех наблюдений (или для выбранных наблюдений при проведении кросс-проверки).

Априорные вероятности классификации.
Априорные вероятности классификации.

Имеется одно дополнительное обстоятельство, которое следует рассмотреть при классификации образцов. Иногда вы знаете заранее, что в одной из групп имеется больше наблюдений, чем в другой. Поэтому априорные вероятности того, что образец принадлежит такой группе, выше. Например, если вы знаете заранее, что 60% выпускников вашей средней школы обычно идут в колледж, (20% идут в профессиональные школы и остальные 20% идут работать), то вы можете уточнить предсказание таким образом: при всех других равных условиях более вероятно, что учащийся поступит в колледж, чем сделает два других выбора.


Вы можете установить различные априорные вероятности, которые будут затем использоваться для уточнения результатов классификации наблюдений (и для вычисления апостериорных вероятностей).

На практике, исследователю необходимо задать себе вопрос, является ли неодинаковое число наблюдений в различных совокупностях в первоначальной выборке отражением истинного распределения в популяции, или это только (случайный) результат процедуры выбора. В первом случае вы должны положить априорные вероятности пропорциональными объемам совокупностей в выборке; во втором - положить априорные вероятности одинаковыми для каждой совокупности. Спецификация различных априорных вероятностей может сильно влиять на точность классификации.

Итог классификации.
Итог классификации.

Общим результатом, на который следует обратить внимание при оценке качества текущей функции классификации, является матрица классификации. Матрица классификации содержит число образцов, корректно классифицированных (на диагонали матрицы) и тех, которые попали не в свои совокупности (группы).

Другие предостережения.
Другие предостережения.

При повторной итерации апостериорная классификация того, что случилось в прошлом, не очень трудна. Нетрудно получить очень хорошую классификацию тех образцов, по которым была оценена функция классификации. Для получения сведений, насколько хорошо работает процедура классификации на самом деле, следует классифицировать (априорно) различные наблюдения, то есть, наблюдения, которые не использовались при оценке функции классификации. Вы можете гибко использовать условия отбора для включения или исключения из вычисления наблюдений, поэтому матрица классификации может быть вычислена по "старым" образцам столь же успешно, как и по "новым". Только классификация новых наблюдений позволяет определить качество функции классификации (см. также кросс-проверку); классификация старых наблюдений позволяет лишь провести успешную диагностику наличия выбросов или области, где функция классификации кажется менее адекватной.

Итог.
Итог.

В общем, Дискриминантный анализ - это очень полезный инструмент (1) - для поиска переменных, позволяющих относить наблюдаемые объекты в одну или несколько реально наблюдаемых групп, (2) - для классификации наблюдений в различные группы.

В начало

(c) Copyright StatSoft, Inc., 1984-2001
STATISTICA является торговой маркой StatSoft, Inc.

---

---