Пример из области медицины

18.1 Пример из области медицины

Обратимся ещё раз к примеру, который уже приводился при рассмотрении логистической регрессии. В этом примере приводятся выборочные данные о пациентах с нарушениями работы легких. Эти данные хранятся в файле lunge.sav. Приведем ещё раз переменные, которые в данном случае будут применяться при дискриминантом анализе:

Имя переменной	Значение
out	Исход (0 = скончался, 1 = выжил)
alter	Возраст
bzeit	Время проведения искусственного дыхания в часах
kob	Концентрация кислорода в смеси для искусственного дыхания
адд	Интенсивность искусственного дыхания
geschl	Пол (1 = мужской, 2 = женский)
gr	Рост

Переменная out делит пациентов на две группы; при помощи остальных переменных предстоит прогнозировать принадлежность к одной из групп.

Откройте файл lunge.sav.

Выберите в меню Analyze (Анализ) Classify (Классифицировать) Discriminant... (Дискриминантный анализ)

Откроется диалоговое окно Discriminant Analysis (Дискриминантный анализ).

Пример из области социологии

18.2 Пример из области социологии

В своём исследовании "Культурный прорыв. Изменение ценностей в западном мире" (см. дополнительную литературу) Рональд Инглехарт (Ronald Inglehart) приводит тезис, что в более зрелых возрастных группах значимо большее количество человек высказались в пользу материальных ценностей (см. гл. 8.4.2). Среди младших поколений, согласно Инглехарту, растёт доля постматериалистов. Склонность опрошенных к постматериалистическим ценностям зависит от их образования и профессиональной квалификации. Чем выше образование и профессиональная квалификация, тем выше склонность к постматериалистическим ценностям. Значение имеет также и социально-экономический статус отца; согласно мнению Инглехарта, чем он выше, тем значительней доля постматериалистов. При помощи дискриминантного анализа мы проверим эту теорему смены ценностей, сформулированную американским политологом.

Откройте в редакторе данных файл postmat.sav.

Переменные, которые вы сможете найти в этом файле, приводятся в нижеследующей таблице.

Имя переменной	Значение
ingMnd	Индекс Инглехарта
	Ценности:
	1 Постматериалисты
	2 Постматериалисты смешанного типа
	3 Материалисты смешанного типа
	4 Материалисты
	5 Не могу дать ответ
	6 Нет данных
statpaps	Социально-экономический статус отца (индекс)
	Значения:
	1 Низкий
	5 Высокий
	8 Формируется в данный момент (отсутствующее значение)
	9 Безработный, в заключении, умер, пенсионер и т.д. (отсутствующее
	значение)
schule	Уровень образования опрашиваемых
	Значения:
	1 Без образования
	2 Начальная школа
	3 Незаконченное среднее
	4 Среднее
alter	Возраст опрашиваемых
	Значения:
	1 18 до 29 лет
	2 30 до 44 лет
	3 45 до 59 лет
	4 60 до 74 лет
	5 75 до 88 лет
	6 89 и старше
	9 Не указан (отсутствующее значение)
ausbild	Профессиональное образование опрашиваемых Значения: 0 Образование отсутствует (отсутствующее значение) 1 Краткосрочное образование 2 Ученик 3 Мастер/техник 4 Высшее образование

Прежде чем преступить к дискриминантному анализу, преобразуем сначала переменную ingl_ind к дихотомическому типу. Значения признаков: 1 ("Постматериалисты") и 2 ("Постматериалисты смешанного типа") должны бить включены в новое значение признака 1 ("Постматериалистические типы") переменной ingMnd, а значения признаков: 3 ("Материалисты смешанного типа") и 4 ("Материалисты") в новое значение признака 2-"Материалистические типы".

Для этого в редакторе синтаксиса введите следующие команды:

RECODE ingl_ind (1,2 = 1) (3,4 = 2)

INTO ingl_dic. VARIABLE LABELS

ingl_dic = "Inglehart-Index, dichotom".

VALUE LABELS

ingl_dic 1 "Postmat. Typen"

2 "Materialist.Typen".

EXECUTE.

Вы можете также загрузить в редактор синтаксиса и файл ingledic.sps, в котором находятся эти команды.

Пометьте команды и запустите программу щелчком на кнопке Run Current (Выполнить текущие команды).

В редакторе данных появится новая переменная ingl_dic. Теперь проведите дискриминантный анализ.

Выберите в меню опции Analyze (Анализ) Classify (Классифицировать) Discriminant... (Дискриминантный анализ)

Переменную ingl_dic поместите в поле групповых переменных.

Щёлкните на выключателе Define Range... (Определить область) и в качестве минимального значения введите 1, а в качестве максимального значения 2.

Переменные statpaps, schule, alter и ausbild поместите в список Independents (Независимые переменные). Оставьте метод ввода переменных Enter independents together (Независимые переменные вводить одновременно), установленный по умолчанию.

Диалоговое окно Discriminant Analysis (Дискриминантный анализ) должно теперь выглядеть так, как показано на рисунке 18.4.

Пример из области биологии

18.3 Пример из области биологии

Дискриминантный анализ очень часто применяется для обработки данных из области биологии. В следующем типичном примере для некоторого количества индивидуумов принадлежность к группе уже известна, на основании чего и строится дискриминантная функция. Далее она используется для того, чтобы оценить принадлежность к определенной группе тех индивидуумов, для которых она ещё не известна.

В файле vogel.sav хранятся данные о половой принадлежности, длине крыла, длине клюва, размере головы, длине лап и весе 245 птиц определённого вида. Причём пол смогли определить только для 51 особи. Кодировка пола соответствует 1 = мужской и 2 = женский; отсутствие данных кодируется 9.

Если для перечисленных параметров Вы рассчитаете средние значения для самцов и самок, то для самок получите более высокие показатели. Исходя из этого, при помощи дискриминантного анализа можно попытаться определить пол тех особей, для которых этого нельзя было сделать ранее.

Откройте файл vogel.sav.

В диалоговом окне Discriminant Analysis (Дискриминантный анализ) переменной geschl (Пол) присвойте статус групповой переменной с пределами от 1 до 2, а переменным fluegel (Длина крыла), schnl (Длина клюва), kopfl (Размер головы), fuss (Длина лап) и gew (Вес) — статус независимых переменных. Выберите пошаговый метод.

В диалоговом окне Discriminant Analysis: Classify (Дискриминантный анализ: Классифицировать) активируйте Casewise results (Результаты для отдельных наблюдений) с ограничением в 40 наблюдений и Summary table (Сводная таблица).

Через выключатель Save... (Сохранить) при помощи активирования опций Predicted group membership (Прогнозируемая принадлежности к группе) и Probabilities of group membership (Вероятности принадлежности к группе) затребуйте генерирование соответствующих переменных.

Из всех результатов, приводимых в окне просмотра, в книге рассматриваются только статистики для каждого наблюдения. По классификационной таблице видно, что для 51 наблюдения с заранее известным полом 44 раза, т.е. в 86,3 % наблюдений, пол был спрогнозирован верно (см. следующую таблицу).

Если мы рассмотрим наблюдение 8, то здесь пол известен — женский и в результате прогноза получается женский пол, а вот для наблюдения 30 пол известен как мужской, но прогнозируется как женский. Наблюдения с нераспознанным полом приводятся в таблице как "ungrouped" (не группированные).

Для наблюдения 1, для которого пол оказался неизвестным, он прогнозируется как женский. Значение вероятности прогнозирования, 0,990, указывается в колонке "P(G=g | D=d)" под заголовком "Highest Group" (Старшая группа). Менее достоверным является прогноз пола для наблюдения 10, здесь вероятность прогнозирования составляет только 0,721.

Casewise Statistics

(Статистики для наблюдений)
	Case Number (Номер случая)	Actual Group (Факти-ческая группа)	Highest Group (Старшая группа)	Second Highest Group (Вторая по старшинству группа)	Discri-minant Scores (Значе-ния диск-рими- нантной фун-кции)
Predicted Group (Прог-нози- руемая группа)	P(D>d \| e=g)	P(G=9 I D=d)	Squared Ma-hala-nobis Distance to Cent-raid (Квадрат рас-стояния Маха-ланобиса до цент-роида)	Group (Груп-па)	P(G=g \|D=d)	Squared Ма-halanobis Distance to Centraid (Квадрат рас-стояния Маха-ланобиса до центро-ида)	Fun-ction 1 (Фун-кция 1 )
P	df
Original (Пер- вона- чаль -но)	1	ungrouped (не груп-пирова-нный)	2	,222	1	,990	1,489	1	,010	10,679	2,304
2	ungrouped (не груп-пирова-нный)	2	,063	1	,997	3,453	1	,003	15,254	2,942
3	ungrouped (не груп-пирова-нный)	2	,064	1	,997	3,433	1	,003	15,213	2,937
4	ungrouped (не груп-пирова-нный)	2	,245	1	,989	1,353	1	,011	10,307	2,247
5	ungrouped (не груп-пирова-нный)	2	,126	1	,995	2,338	1	,005	12,792	2,613
6	ungrouped (не груп-пирова-нный)	2	,319	1	,984	,995	1	,016	9,271	2,081
7	ungrouped (не груп-пирова-нный)	2	,485	1	,971	,489	1	,029	7,543	1,783
8	2	2	,102	1	,996	2,673	1	,004	13,561	2,719
9	ungrouped (не груп-пирова-нный)	2	,387	1	,980	,748	1	,020	8,482	1,949
10	ungrouped (не группирова-нный)	2	,576	1	,721	,313	1	,279	2,213	,524
11	ungrouped (не груп-пирова-нный)	2	,651	1	,954	,205	1	,046	6,248	1,536
12	ungrouped (не груп-пирова-нный)	2	,140	1	,994	2,177	1	,006	12,411	2,559
13	ungrouped (не груп-пирова-нный)	2	,435	1	,976	,609	1	,024	7,995	1,864
14	ungrouped (не группиро-ванный)	2	,471	1	,973	,519	1	,027	7,662	1,804
15	ungrouped (не группиро-ванный)	2	,764	1	,938	,090	1	,062	5,510	1,384
16	ungrouped (не группиро-ванный)	2	,481	1	,972	,497	1	,028	7,576	1,789
17	ungrouped (не груп-пирова-нный)	2	,172	1	,993	1,868	1	,007	11,658	2,451
18	2	2	,399	1	,979	,712	1	,021	8,359	1,928
19	ungrouped (не груп-пирова-нный)	2	,705	1	,946	,143	1	,054	5,884	1,462
20	2	2	,969	1	,898	,002	1	,102	4,355	1,123
21	2	2	,249	1	,989	1,328	1	,011	10,238	_ 2,236
22	ungrouped (не груп-пиров-анный)	2	,121	1	,995	2,407	1	,005	12,953	2,636
23	2	2	,071	1	,997	3,263	1	,003	14,853	2,890
24	ungrouped (не груп-пирова-нный)	2	,367	1	,981	,815	1	,019	8,704	1,987
25	ungrouped (не груп-пиров-анный)	2	,880	1	,857	,023	1	,143	3,598	,933
26	ungrouped (не груп-пирова-нный)	2	,537	1	,966	,382	1	,034	7,103	1,702
27	ungrouped (не группиро-ванный)	1	,640	1	,955	,218	2	,045	6,323	-1,431
28	2	2	,744	1	,806	,107	1	,194	2,960	,757
29	ungrouped (не груп-пирова-нный)	2	,969	1	,883	,001	1	,117	4,035	1,045
30	1	2"	,625	1	,749	,239	1	,251	2,428	,595
	31	ungrouped (не груп-пирова-нный)	2	,646	1	,760	,211	1	,240	2,521	,624
32	2	2	,173	1	,993	1,860	1	,007	11,636	2,448
33	1	2"	,504	1	,970	,447	1	,030	7,378	1,753
34	ungrouped (не груп-пирова-нный)	2	,544	1	,966	,368	1	,034	7,046	1,691
35	ungrouped (не груп-пирова-нный)	2	,618	1	,958	,248	1	,042	6,480	1,582
36	ungrouped (не груп-пирова-нный)	2	,727	1	,943	,122	1	,057	5,744	1,433
37	2	2	,458	1	,974	,551	1	,026	7,781	1,826
38	2	2	,362	1	,981	,829	1	,019	8,750	1,995
39	2	2	,814	1	,929	,055	1	,071	5,211	1,319
40	ungrouped (не груп-пирова-нный)	2	,812	1	,930	,057	1	,070	5,222	1,322

** Misclassified case (** - Неверно классифицированный случай)

Для того, чтобы хотя бы частично сократить количество ошибочных значений для переменной пола, при анализе вы можете применять прогнозируемую групповую принадлежность только в тех случаях, для которых вероятность прогнозирования принимает некоторое минимально допустимое значение, к примеру, 0,9.

IF (dis_1 = 1 and disl_1 >= 0,9)

geschl=1

. IF (dis_1 = 2 and dis2_1 >= 0,9)

geschl=2.

EXECUTE.

Таким образом, в используемом примере можно присвоить половой показатель ещё 90-а птицам. Если вы снизите минимально допустимое значение вероятности прогнозирования, то это число станет ещё больше.

К файлу были добавлены три новые переменные:

dis_1: Прогнозируемая группа

disl_1: Вероятность принадлежности к группе 1

dis2_1: Вероятность принадлежности к группе 2.

Пример из области биологии (три группы)

18.4 Пример из области биологии (три группы)

В предыдущих примерах дискриминантный анализ всегда проводился при наличии лишь двух групп. В этой главе рассматривается пример, в котором групповая переменная имеет больше двух категорий, а именно три.

В файле kaefer.sav содержатся данные о длине и ширине грудной клетки трёх видов жуков (обозначенных как А, В и С). Если вы проведёте однофакторный дисперсионный анализ с последующими дополнительными тестами (Post-hoc-Tests), то увидите, что три разновидности жуков очень значимо различаются между собой как по длине, так и по ширине, поэтому вполне можно предположить, что этих жуков можно классифицировать между упомянутыми видами на основании их длины и ширины посредством дискриминантного анализа.

Откройте файл kaefer.sav.

Вы увидите, что 17 жуков из 30 не отнесены ни к иной из групп; поэтому классификация жуков по группам должна быть произведена при помощи дискриминантного анализа.

В диалоговом окне Discriminant Analysis (Дискриминантный анализ) переменной kaefer (Жук) присвойте статус групповой переменной с пределами от 1 до 3, а переменным laenge (Длина) и breite (Ширина) статус независимых переменных. Оставьте активной установку по умолчанию Enter independents together (Независимые переменные вводить одновременно).

В диалоговом окне Discriminant Analysis: Statistics (Дискриминантный анализ: Статистики) в разделе Descriptives (Дискриптивние статистики) активируйте опции: Means (Средние значения), Univariate ANOVAs (Одномерные тесты ANOVA) и в разделе Function Coefficients (Коэффициенты функции) опцию Unstandardized (He стандартизированные).

В диалоговом окне Discriminant Analysis: Classify (Дискриминантный анализ: Классифицировать) сделайте запрос на Case-wise results (Результаты для отдельных наблюдений) и Summary table (Сводную таблицу) и в разделе Plots (Графики) активируйте опцию Territorial map (Территориальная карта). Эта опция служит для построения классификационной диаграммы, так называемой территориальной карты (Territorial map). Построение этой диаграммы типично для случая с более чем двумя группами.

В заключение, в диалоговом окне Discriminant Analysis: Save (Дискриминантный анализ: Сохранить), активируйте все опции, находящиеся там, с целью создания соответствующих переменных в исходном файле.

Из всей гаммы приводимых результатов расчёта мы рассмотрим только самые важные. Из групповых статистик можно узнать, что в семейство А входят самые большие, а в семейство В самые маленькие жуки.

Group Statistics

(Статистики для групп)
KAEFEP (Жук)	Mean (Сред-нее значе-ние)	Std. Deviation (Станда-ртное отклоне-ние)	Valid N (listwise) (Действительные значения (по списку))
Unweighted (Не взвеше-нное)	Weighted (Взвеше-нное)
1 (Семейство А)	LAENGE (Длина)	1 ,6226	5.968Е-02	42	42,000
BREITE (Ширина)	1 ,2607	4J54E-02	42	42,000
2 Семейство В)	LAENGE (Длина)	1 ,3089	7.634Е-02	45	45,000
BREITE (Ширина)	1,0122	4.415Е-02	45	45,000
3 Семейство С)	LAENGE (Длина)	1,4788	6.029Е-02	26	26,000
BREITE (Ширина)	1,1192	5.114Е-02	26	26,000
Total	LAENGE (Длина)	1,4646	,1535	113	113,000
BREITE (Ширина)	1,1292	,1191	113	113,000

Статистика Лямбда Уилкса (>i) свидетельствует о том, что жуки очень значимо делятся на группы как по длине, так и по ширине.

Tests of Equality of Group Means (Тест на равенство средних значений групп)

	Wilks' Lambda (Лямбда Уилкса)	F	df1	df2	Sig. (Значимость)
LAENGE (Длина)	,187	239,154	2	110	,000
BREITE (Ширина)	,153	303,326	2	110	,000

Если насчитывается более двух классификационных групп, то можно образовать больше одной дискриминантной функции; при трёх группах, как в приведенном примере, их будет две. Следующая таблица свидетельствует о том, что обе дискриминантные функции дают значимые результаты для разделения между группами и, следовательно, могут быть использованы соответствующим образом. Однако, первая функция дает вероятность прогноза 98,7 %, а вторая только 1,3 %.

Eigenvalues (Собственные значения)

Function (Функция)	Eigenvalue (Собствен-ные значение)	% of Variance (% диспер-сии)	Cumulative % (Совокуп-ный %)	Canonical Correlation (Канони-ческая корре-ляция)
1	6,040а	98,7	98,7	,296
2	,078а	1,3	100,0	,269

a. First 2 canonical discriminant functions were used in the analysis (В этом анализе используются первые 2 канонические дискриминантные функции).

Wilks' Lambda (Лямбда Уилкса)

Test of Function(s) (Тест функции (й))	Wilks1 Lambda (Лямбда Уилкса)	Chi-square (Хи-квадрат)	df	Sig. (Значимость)
1 through 2 (1 до 2)	,132	221,900	4	,000
2	,928	8,202	1	,004

Затребованные нестандартизированные коэффициенты функций приводятся в следующей таблице.

Canonical Discriminant Function Coefficients

(Канонические коэффициенты дискриминантных функций)
	Function (Функция)
1	2
LAENGE (Длина)	5,831	18,769
BREITE (Ширина)	14,891	-23,659
(Constant) (Константа)	-25,355	-,773

Unstandardized coefficients (Нестандартизированные коэффициенты)

Мы здесь опускаем вывод статистик для каждого отдельного случая. В результате расчетов Вы получаете соответствующие номера групп и вероятность прогнозирования под заголовком P(G = g|D = d). Прогнозирование осуществлено и для 17 неклассифицированных случаев.

На территориальной карте показано разделение на области, которые означают принадлежность к группе. При этом в пределах границ соответствующей области вероятность отнесения к данной группе выше, чем для других групп. На границах областей вероятности для граничащих групп одинаковы.

Значения обеих дискриминантных функций, на основе которых построена эта территориальная карта, Вы можете увидеть в редакторе данных под именами двух вновь созданных переменных: dis1_1 и dis2_1.

В заключение приводится обзор результатов классификации. По ним Вы можете заметить, что прогноз для групп А и В практически полностью был сделан верно и корректно классифицированы, в общей сложности, 91,2 % всех случаев.

Classification Results a

(Результаты Классификации)
	FUND (Семе-йство)	Predicted Group Membership	Total (Сум-ма)
1 (Семей-ство А)	2 (Семей-ство В)	3 (Семей-ство С)
Original (Перво-нача-льно)	Count (Коли-чество)	1 (Семейство А)	41	0	1	42
2 (Семейство В)	0	43	2	45
3 (Семейство С)	4	3	19	26
Ungrouped cases (He груп-пирован-ные случаи)	7	6	4	17
%	1 (Семейство А)	97,6	,0	2,4	100,0
2 (Семейство В)	,0	95,6	4,4	100,0
3 (Семейство С)	15,4	11,5	73,1	100,0
Ungrouped cases (He груп-пирован-ные случаи)	41,2	35,3	23,5	100,0

а. 91,2% of original grouped cases correctly classified (91,2 % первоначально сгруппированных случаев были классифицированы корректно).

Символы, используемые втерриториальной карте
Символ	Группа	Метка
1 2 3	1 2 3	Семейство А Семейство В Семейство С
Маркировка	Центроиды групп

Наряду с уже упоминавшимися значениями обеих дискриминантных функции в редакторе данных были созданы: переменная dis_1, содержащая значение прогнозируемой группы и переменные disl_2, dis2_2 и dis3_2, которые содержат прогнозируемые вероятности отнесения к одной из трёх групп. Группа, которой соответствует наибольшая вероятность прогнозирования и есть прогнозируемая группа.

Диалоговое окно Discriminant Analysis: Classification (Дискриминантный анализ: Классификация)

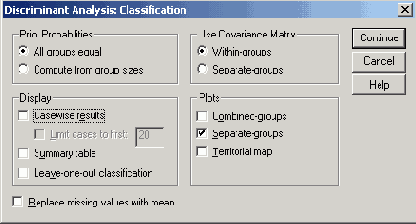
Сделайте здесь запрос на Summary table (Сводную таблицу).

Щёлкните на выключателе Save... (Сохранить). Откроется диалоговое окно Discriminant Analysis: Save (Дискриминантный анализ: Сохранить) (см. рис. 18.7).

Диалоговое окно Discriminant Analysis (Дискриминантный анализ).

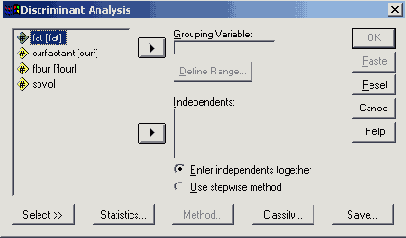
Поместите переменную out в поле, предназначенное для групповых переменных.

После щелчка по выключателю Define Range... (Определить промежуток) введите минимальное и максимальное значения этой переменной: 0 и 1.

Переменным agg, alter, bzeit, gcschl, gr и kob присвойте статус независимых переменных. Для начала оставим установленный по умолчанию метод: Enter independents together (Одновременный учет всех независимых переменных), при котором в анализе одновременно будут участвовать все независимые переменные.

После щелчка по выключателю Statistics... (Статистики) активируйте опции: Means (Средние значения), Univariate ANOVAs (Одномерные тесты ANOVA), Unstandardized Function Coefficients (Нестандартизированные коэффициенты функции) и Within-groop Correlation Matrice (Корреляционная матрица внутри группы).

Через выключатель Classify (Классифицировать) сделайте дополнительно запрос на вывод диаграмм по отдельным группам (Separate-groups Plots), результатов для отдельных наблюдений (Casewise results) и сводной таблицы (Summary table). При выводе результатов для отдельных наблюдений ограничимся первыми двадцатью, поместив этот предел в соответствующую позицию диалогового окна.

Довольно полезный график для объединенных групп, который был реализован в ранних версиях SPSS, и сейчас можно активировать в диалоговом окне, однако вместо графика в окне отображения результатов будет появляться предупреждение о том, что такая гистограмма в анализах более не доступна.

При помощи выключателя Save... (Сохранить) активируйте сохранение значения дискриминантной функции в дополнительной переменной (Discriminant Scores).

Начните расчёт нажатием ОК.

После вводного обзора действительных и пропущенных значений приводятся средние значения, стандартные отклонения, количество наблюдений для каждой группы в отдельности и суммарные показатели для обеих групп.

Переменная geschl является при этом дихотомической переменной, принадлежащей к номинальной шкале с кодировками: 1 (мужской пол) и 2 (женский пол). Средние значения пола для обоих групп по исходу Легения, кажущиеся на первый взгляд бесполезными, равны 1,63492 и 1,45588; если бы вместо этого переменные были закодированы при помощи 0 и 1, то оба средних значения равнялись бы 0,63492 и 0,45588 соответственно. Для таких дихотомических переменных, кодированных при помощи 0 и 1, среднее значение указывает на долю наблюдений с кодировкой 1. Это означает, что для группы "скончался" доля женщин в процентном отношении составляет 63,492, а для группы "выжил" 45,588.

Group Statistics (Статистики для групп)
Outcome (Исход)	Mean (Среднее значение)	Std. Deviation (Стандартное отклонение)	Valid N (listwise) (Действительные значения (по списку))
Unwe-ighted (Не взвешено)	Weig-hted (Взве-шено)
gesto-rben (Скон-чался)	Aggressivitaet der Beatmung (Интенси-вность искус-ственного дыхания)	15,90013	10,90013	63	63,000
ALTER (Возраст)	31,92063	13,82529	63	63,000
Beatmungszeit in Std. (Время проведения искус-ственного дыхания в часах)	15,36508	10,50085	63	63,000
Geschlecht (Пол)	1,63492	,48532	63	63,000
Koerper-groesse (Рост)	165,1429	15,55931	63	63,000
Sauerstoff-Konzentration (Концент-рация кислорода в смеси для искус-ственного дыхания)	,85952	,14807	63	63,000
ueberlebt (Выжил)	Aggressivitaet der Beatmung (Интенси-вность искус-ственного дыхания)	11,69699	8,16057	68	68,000
ALTER (Возраст)	27,97059	10,86411	68	68,000
Beatmungszeit in Std. (Время проведения искус-ственного дыхания в часах)	10,79412	5,10065	68	68,000
Geschlecht (TlonJ	1,45588	,50175	68	68,000
Koerpe-rgroesse (Рост)	172,0588	11,01137	68	68,000
Sauerstoff-Konzentration (Концентрация кислорода в смеси для искус-ственного дыхания)	,80338	,15493	68	68,000
Total	Aggressivitaet der Beatmung (Интенси-вность искус-ственного дыхания)	13,51843	9,72600	131	131,000
ALTER (Воз_раст)	29,87023	12,48654	131	131,000
Beatmungszeit in Std. (Время проведения искус-ственного дыхания в часах)	12,99237	8,44120	131	131,000
Geschlecht (Пол)	1,54198	,50015	131	131,000
Koerpe-rgroesse (Рост)	168,7328	13,78339	131	131,000
Sauerstoff-Konzentration (Конце-нтрация кислорода в смеси для искус-ственного дыхания)	,83038	,15369	131	131,000

Затем проводится тест, насколько значимо различаются между собой переменные в обеих группах; наряду с тестовой величиной, в качестве которой служит Лямбда Уилкса ("Wilks-Lambda"), применяется также и простой дисперсионный анализ. Для всех переменных (кроме возраста, для которого однако также просматривается сильная тенденция к значимости) получается значимое различие между обеими группами:

Tests of Equality of Group Means (Тест равенства групповых средних значений)

	Wilks Lambda (Лямбда Уилкса)	F	df1	df2	Sig. (Значи-мость)
Aggressivitaet der Beatmung (Интенсивность искусственного дыхания)	,962	5,116	1	129	,025
ALTER (Возраст)	,975	3,331	1	129	,070
Beatmungszeit in Std. (Время проведения искусственного дыхания в часах)	,926	10,273	1	129	,002
Geschlecht (Пол)	,968	4,297	1	129	,040
Koerpergroesse (Рост)	,937	8,722	1	129	,004
Sauerstoff-Konzentration (Концентрация кислорода в смеси для искусственного дыхания)	,966	4,481	1	129	,036

Далее следует корреляционная матрица между всеми переменными, в которой приводятся коэффициенты, осредненные для обеих групп:

Pooled Within-Groims Matrices (Объединённые внутригрупповые матрицы)

	Aggres-sivitaet der Beat-mung (Интен-сивность искус-ственного дыхания)	ALTER (Воз-раст)	Beatmun-gszeit in Std. (Время прове-дения искус-ственного дыхания в часах)	Gesc-hlecht (Пол)	Koerper-groesse (Рост)	Saue-rstoff- Konzen-tration (Концен-трация кисл-орода в смеси для искус-ственного дыхания)
Corre-lation (Корре-пяция)	Aggres-sivitaet der Beatmung (Интен-сивность искус-ственного дыхания)	1,000	-,072	-,058	,141	-,042	,285
ALTER (Возраст)	-,072	1,000	,093	-,040	,277	-.119
Beatmu-ngszeit in Std. (Время прове-дения искус-ственного дыхания в часах)	-,058	,093	1,000	,069	-,126	-,089
Geschlecht (Пол)	.141	-0,40	,069	1,000	-,481	-,066
Koerpe-rgroesse (Рост)	-,042	,277	-,126	-,481	1,000	,000
Sauer-stoff-Konze-ntration (Конце-нтрация кисло-рода в смеси для искус-ственного дыхания)	,285	-,119	-,089	-,066	,000	1,000

Следующими шагами являются расчёт и анализ коэффициентов дискриминантной функции. Значения этой функции должны как можно отчётливей разделять обе группы. Мерой удачности этого разделения служит корреляционный коэффициент между рассчитанными значениями дискриминантной функции и показателем принадлежности к группе:

Eigenvalues (Собственные значения)

Function (Функция)	Eigenvalue (Собственное значение)	% of Variance (% дисперсии)	Cumulative % (Сово-купный %)	Canonical Correlation (Канони-ческая корреляция)
1	,256"	100,0	100,0	,452

a. First 1 canonical discriminant functions were used in the analysis (В этом анализе используются первые 1 канонические дискриминантные функции).

Wilks' Lambda (Лямбда Уилкса)

Test of Function(s) (Тест функции (и))	Wilks' Lambda (Лямбда Уилкса)	Chi-square (Хи-квадрат)	df	Sig. (Значимость)
1	,796	28,733	6	,000

Судя по значению коэффициента, равному 0,452, корреляция абсолютно не удовлетворительная. При помощи Лямбда Уилкса производится тест на то, значимо ли в обеих группах отличаются друг от друга средние значения дискриминантной функции; в приводимом примере, значение р < 0,001, указывает на очень значимое различие.

Значение, выводимое под именем "Eigenvalue" (Собственное значение), соответствует отношению суммы квадратов между группами к сумме квадратов внутри групп. Эти две суммы Вы сможете получить, если проведете дисперсионный анализ значений дискриминантной функции (переменная dis1_1) по фактору out (см. гл. 13.3). Большие собственные значения (в данном случае такого, к сожалению, не наблюдается) указывают на "хорошие" (удачно подобранные) дискриминантные функции.

Следующая таблица дает представление о том, как сильно отдельные переменные, применяемые в дискриминантной функции, коррелируют со стандартизированными значениями этой дискриминантной функции. При этом корреляционные коэффициенты были рассчитаны в обеих группах по отдельности и затем усреднены:

Standardized Canonical Discriminant Function Coefficients

(Стандартизиро-ванные канонические коэффициенты дискриминантной функции)
	Function (Функция)
1
Aggressivitaet der Beatmung (Интенсивность искусственного дыхания)	,316
ALTER (Возраст)	,494
Beatmungszeit in Std. (Время проведения искусственного дыхания в часах\|	,491
Geschlecht (Пол)	,066
Koerpergroesse (Рост)	-,544
Sauerstoff-Konzentration (Концентрация кислорода в смеси для искусственного дыхания)	,385

Structure Matrix

(Структурная матрица)
	Function (Функция)
1
Beatmungszeit in Std. (Время проведения искусственного дыхания в часах)	,558
Koerpergroesse (Рост)	-,514
Aggressivitaet der Beatmung (Интенсивность искусственного дыхания)	,393
Sauerstoff-Konzentration (Концентрация кислорода в смеси для искусственного дыхания)	,368
Geschlecht (Пол)	,361
ALTER (Возраст)	,318

Pooled within-groups correlations between discriminating variables and standardized canonical discriminant functions (Объединённые корреляции внутри групп между диск-риминантными переменными и стандартизированными каноническими дискриминант-ными функциями).

Variables ordered by absolute size of correlation within function (Переменные расположены в соответствии с абсолютными корреляционными величинами внутри функции).

И в заключение, приводятся сами коэффициенты дискриминантной функции:

Canonical Discriminant Function Coefficients

(Канонические коэффициенты дискриминантной функции)
	Function (Функция)
1
Aggressivitaet der Beatmung (Интенсивность искусственного дыхания)	,033
ALTER (Возраст)	,040
Beatmungszeit in Std. (Время проведения искусственного дыхания в часах)	,060
Geschlecht (Пол)	,133
Koerpergroesse (Рост)	-,041
Sauerstoff-Konzentration (Концентрация кислорода в смеси для искусственного дыхания)	2,539
(Constant)	2,121

Unstandardized coefficients (Нестандартизированные коэффициенты)

Здесь речь идёт о нестандартизированных коэффициентах — это множители при заданных значениях переменных, входящих в дискриминантную функцию. Стандартизированные коэффициенты, которые приводились ранее, основаны на стандартизированных значениях переменных, получаемых с помощью z-преобразования.

Далее приводятся средние значения дискриминантной функции в обеих группах:

Functions at Group Centroids

(Функции групповых центроидов)
Outcome (Исход)	Function (функция)
1
gestorben (Скончался)	,522
ueberlebt (Выжил)	-,483

Unstandardized canonical discriminant functions evaluated at group means (Heстандартизированные канонические дискриминантные функции, которые оцениваются по групповым средним значениям).

Далее следует таблица, в которой построчно для каждого наблюдения приводится информация о значении дискриминантной функции и определяется принадлежность к одной из двух групп. Мы здесь ограничились первыми двадцатью наблюдениями.

Группа, к которой фактически принадлежит наблюдение, отображается в колонке с именем "Actual Group" (Фактическая группа). В следующих трёх колонках содержится информация о прогнозе принадлежности к группе, сделанном на основании значения дискриминантной функции. Сначала приводится прогнозируемая принадлежность к группе; если она не соответствует фактической принадлежности, то в колонке "Predicted Group" (Прогнозируемая группа) отображаются две звёздочки (**).

Casewise Statistics

(Статистики для наблюдений)
	Case Number (Поряд-ковый номер случая)	Actual Group (Факти-ческая груп-па)	Highest Group (Старшая группа)	Second Highest Group (Вторая по старшинству группа)	Discri-minant Scores (Значе-ния дискри-ми- нант-ности)
Predic-ted Group (Прогно-зируе-мая груп-па)	P(D>d G=g)	P(G=g \| D=d)	Squared Maha-lanobis Distance to Centroid (Квадрат рас-стояния Махапа-нобиса до центро-ида)	Group (Груп-па)	P(G=g \|D=d)	Squared Maha-lanobis Distance to Centroid (Квадрат рас-стояния Маха-ланобиса до центро-ида)	Function 1 (Фун-кция 1)
р	df	1
Origi-nal (Перво-нача-льно)	1	0	1"	,727	1	,702	,122	0	,298	1,834	-.833
2	1	0"	,116	1	,889	2,464	1	,111	6,631	2,092
3	0	1"	,842	1	,576	,040	0	,424	,650	-,284
4	1	1	,310	1	,821	1,032	0	,179	4,085	-1,499
5	1	1	,495	1	,767	,465	0	,233	2,846	-1,165
6	1	1	,453	1	,779	,563	0	,221	3,081	-1,234
7	0	1"	,635	1	,728	,225	0	,272	2,189	-,958
8	1	1	,549	1	,752	,359	0	,248	2,575	-1,083
9	1	1	,880	1	,587	,023	0	,413	,729	-,332
10	0	1"	,952	1	,609	,004	0	,391	,893	-,423
11	0	0	,026	1	,940	4,980	1	,060	10,477	2,753
12	1	0"	,618	1	,501	,249	1	,499	,256	,023
13	0	0	,930	1	,603	,008	1	,397	,841	,434
14	1	1	,817	1	,676	,053	0	,324	1,528	-,714
15	1	1	,958	1	,611	,003	0	,389	,908	-,431
16	0	1"	,685	1	,524	,165	0	,476	,359	-,077
17	1	1	,388	1	,798	,745	0	,202	3,492	-1,347
18	0	1"	,763	1	,550	,091	0	,450	,496	-,182
19	1	1	,748	1	,696	,103	0	,304	1,760	-,805
20	0	0	,308	1	,822	1,037	1	,178	4,095	1,540

** Мisciassiriea case (Неправильно классифицированное наблюдение;

Далее выводятся две вероятности. Вторая из этих двух вероятностей, обозначенная P(G=g|D=d), является мерой принадлежности к одной из двух групп. Это вероятность того, что некоторой наблюдение принадлежит к прогнозированной группе, которая рассчитывается на основе подстановки в дискриминантную функцию значений набора переменных, соответствующих данному наблюдению. Вероятность того, что данный наблюдение принадлежит к другой группе получается вычитанием меры принадлежности из 1. Она приводится в колонке с названием "Second Highest Group" (Вторая по старшинству группа). Если мы рассмотрим первый наблюдение, то здесь вероятность того, что данный пациент выживет, рассчитанная на основании значении исходных переменных, равна 0,702 (в действительности он скончался).

Первую из двух рассмотренных вероятностей, получившую название Р (D>d|G=g), называют ещё и условной вероятностью. Это вероятность того, что пациент, принадлежащий к прогнозируемой группе, действительно имеет значения параметров, соответствующие дискриминантной функции или некоторые другие крайние значения.

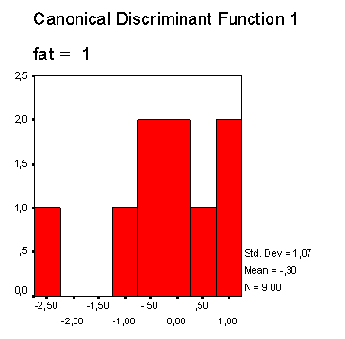
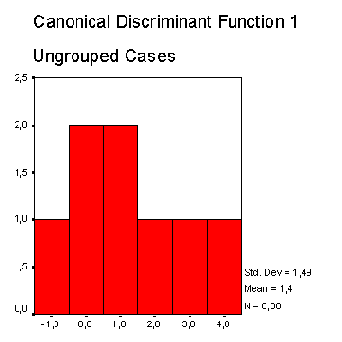
В другой колонке приводится квадрат расстояния Махаланобиса до центроида (среднего значения группы значений дискриминантной функции). В правой колонке таблицы приводится соответствующее значение дискриминантной функции. Распределение значения дискриминантной функции отдельно по группам изображается на двух отдельных гистограммах.

Можно заметить, что значения дискриминантной функции для первой группы (скончался) смещены вправо, а значения второй группы (выжил) — влево, что однако свидетельствует об очень сильном смешении.

В завершении приводится классификационная таблица с указанием достигнутой точности прогнозирования. Значение этой точности равно 68,7 %, что является неудовлетворительным:

Диалоговое окно Discriminant Analysis (Дискриминантный анализ).

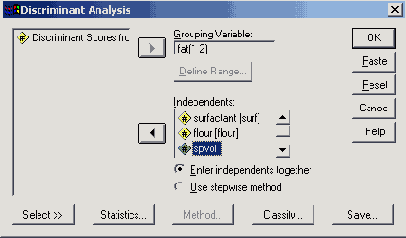
Щёлкните по выключателю Statistics... (Статистики)

Откроется диалоговое окно Discriminant Analysis: Statistics (Дискриминантный анализ: Статистики) (см. рис. 18.5).

Диалоговое окно Discriminant Analysis: Save (Дискриминантный анализ: Сохранить)

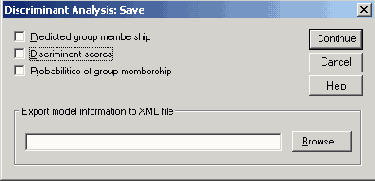
Видно, что в 10 версии появилась возможность сохранения информации о модели в так называемом, XML-файле (см. примечания к рис. 16.3).

Активируйте вывод Predicted group membership (Прогнозируемой принадлежности к группе), Discriminant scores (Значений дисриминантной функции) и Probabilities of group membership (Вероятностей принадлежности к группе).

Подтвердите нажатием Continue (Далее) и затем ОК.

В окне просмотра появится сначала обзор действительных и пропущенных значений:

Analysis Case Processing Summary (Анализ обработанных наблюдений)

Unweighted Cases (He взвешенные случаи)		N	Percent (Процент)
Valid (Действительные)		2200	71,9
Excluded (Исключенные)	Missing or out-of-range group codes (Отсутствующие или находящиеся за пределами допустимой области кодировки принадлежности к группе)	19	,6
At least one missing discriminating variable (По меньшей мере одна отсутствующая дискриминационная переменная)	816	26,7
Both missing or out-of-range group codes and at least one missing discriminating variable (Обе кодировки принадлежности к группе отсутствуют или находятся за пределами допустимой области, или по меньшей мере одна отсутствующая дискриминационная переменная)	23	,8
Total (Общее количество исключённых)	858	28,1
Total (Общее количество случаев)		3058	100,0

В общей сложности 858 наблюдений из 3058, находящихся в файле postmat.sav, были исключены из анализа из-за отсутствия значения переменной ingl_dic или отсутствия значений одной из дискриминационных переменных. Таким образом анализ проводился для 2200 наблюдений. Далее приводятся средние значения, стандартные отклонения и количество наблюдений для всех переменных из обеих групп и для каждой группы в отдельности.

По средним значениям уже заметно, что для постматериалистических типов характерны: более высокий социально-экономический статус отца (2,8148 по сравнению с 2,3904), более высокое образование (2,9853 по сравнению с 2,5248) и принадлежность к младшей возрастной группе (2,1842 по сравнению с 2,8151).

Group Statistics

(Статистики для групп)
INGL_DIC (Индекс Ингпехарта, дихото-мический)		Mean (сред-нее значе-ние)	Std. Deviation (Станда-ртное отклоне-ние)	Valid N (listwise) (Действительные значения (по списку))
Unwei-ghted (Не взвеше-нные)	Weigh-ted (Взвеше-нные)
1,00 (Пост-материа-листический тип)	SES-lndex des Vaters (социально-экономи-ческий статус отца)	2,8148	1,1718	1091	1091,000
Schulabschluss (Образование)	2,9853	,8194	1091	1091,000
ALTER, BEFRAGTE<R>, KATEGORISIERT (Возраст, опрошен-ного(ой), разбит на категории)	2,1842	1,0887	1091	1091,000
Berufsaus-bildung (Профес-сиональное образо-вание)	2,1888	1,1562	1091	1091,000
2,00 (Материа-листический тип)	SES-lndex des Vaters (социально-экономи-ческий статус отца)	2,3904	1,0407	1109	1109,000
Scnulabschluss (Образование)	2,5248	,7627	1109	1109,000
ALTER, BEFRAGTE<R>, KATEGORISIERT (Возраст ,опрошен-ного(ой), разбит на категории)	2,8151	1,2111	1109	1109,000
Berufsa-usbildung (Профес-сиональное образование)	1,8792	1,0249	1109	1109,000
Total (Сумма)	SES-lndex des Vaters (социально-экономи-ческий статус отца)	2,6009	1,1275	2200	2200,000
Schulabschluss (Образование)	2,7532	,8240	2200	2200,000
ALTER, BEFRAGTE<R>, KATEGORI-SIERT (Возраст, опрошен-ного(ой), разбит на категории)	2,5023	1,1942	2200	2200,000
Berufsa-usbildung (Профес-сиональное образование)	2,0327	1,1027	2200	2200,000

Затем проводится тест на значимость различия между переменными, относящимися к обеим группам, то есть выясняется присутствуют ли в них разделяющие (дискриминирующие) особенности, позволяющие судить об отношении к одной из двух групп (постматериалисты — материалисты).

Tests of Equality of Group Means (Тест равенства групповых средних значений)

	Wilks1 Lambda (Лямбда Уилкса)	F	df1	df2	Sig. (Значимость)
SES-lndex des Vaters (социально-экономический статус отца)	,965	80,746	1	2198	,000
Schulabschluss (Образование)	,922	186,281	1	2198	,000
ALTER, BEFRAGTE<R>, KATEGORISIERT (Возраст, опрошенного(ых), разбит на категории)	,930	164,951	1	2198	,000
Berufsausbildung (Профессиональное образование)	,980	44,222	1	2198	,000

Как следует из колонки значимости, по всем переменным наблюдается значительное различие между группами (р < 0,001).

Далее приводится корреляционная матрица между всеми переменными, причём коэффициенты были рассчитаны для обеих групп:

Pooled Within-Groups Matrices (Объединённые матрицы внутри групп)

	SES-lndex des Vaters (социально- экономи-ческий статус отца)	Schulab-schluss (Образо-вание)	ALTER, BEFRAG -TE<R>, KATEGO-RISIERT (Возраст, опрошен-ного(ой), разбит на категории)	Berufsau-sbildung (Профес- сиона-льное образо-вание)
Corre-lation (Корре-ляция)	SES-lndex des Vaters (социально-экономи-ческий статус отца)	1,000	,327	-,033	,137
Schula-bschluss (Образо-вание)	,327	1,000	-,275	,377
ALTER, BEFRA-GTE<R>, KATEGO-RISIERT (Возраст, опрошен-ного(ых), разбит на категории)	-,033	-,275	1,000	,018
Berufsa-usbildung (Профес-сиональное образо-вание)	,137	,377	,018	1,000

Прежде всего, здесь очень заметна корреляция между переменными schule и statpas и между переменными ausbild и schule. Чем выше социально-экономический статус отца, тем выше школьное образование опрашиваемого; чем выше его школьное образование, тем выше и профессиональное образование.

Далее следует анализ коэффициентов дискриминантной функции. Корреляционный коэффициент между рассчитанными значениями дискриминантной функции и реальной принадлежностью к группе, равный 0,353, является неудовлетворительным:

Eigenvalues (Собственные значения)

Function (Функция)	Eigenvalue (Собствен-ное значение)	% of Variance (% диспе-рсии)	Cumulative % (Сово-купный %)	Canonical Correlation (Канони-ческая корре-ляция)
1	,142а	100,0	100,0	,353

a. First 1 canonical discriminant functions were used in the analysis (Первые 1 канонические дискриминантные функции будут применяться в анализе).

Wilks' Lambda (Лямбда Уилкса)

Test of Function(s) Wilks' Lambda (Тест функции (и)) (Лямбда Уилкса)	Chi-square (Хи-квадрат)	df	Sig. (Значимость)
1 ,875	292,431	4	,000

Тест, проведенный с помощью критерия "Лямбда Уилкса" (k), на предмет, значимо ли различаются между собой средние значения дискриминантной функции в обеих группах, показал очень значимый результат (значение р < 0,001).

Затем приводятся стандартизированные коэффициенты дискриминантной функции и их корреляция с используемыми переменными:

Standardized Canonical Discriminant Function Coefficients

(Стандартизиро-ванные канонические коэффициенты дискриминантной функции)
	Function (Функция)
1
SES-lndex des Vaters (социально-экономический статус отца)	,321
Schulabschluss (Образование)	,434
ALTER, BEFRAGTE<R>, KATEGORISIERT (Возраст, опрошенного(ой), разбит на категории)	-,599
Berufsausbildung (Профессиональное образование)	,179

Structure Matrix

(Структурная матрица)
	Function (Функция)
1
Schulabschluss (Образование)	,771
ALTER, BEFRAGTE<R>, KATEGORISIERT (Возраст, опрошенного(ой), разбит на категории)	-,726
SES-lndex des Vaters (социально-экономический статус отца)	,508
Berufsausbildung (Профессиональное образование)	,376

Pooled within-groups correlations between discriminating variables and standardized canonical discriminant functions (Объединённые корреляции внутри групп между дискриминантными переменными и стандартизированными каноническими дискриминант-ными функциями)

Variables ordered by absolute size of correlation within function (Переменные расположены соответственно величине их абсолютных корреляционных показателей).

После этого приводятся нестандартизированные коэффициенты дискриминантной функции и средние значения дискриминантной функции в обеих группах:

Canonical Discriminant Function Coefficients

(Канонические коэффициенты дискриминантной функции)
	Function (Функция)
1
SES-lndex des Vaters (социально-экономический статус отца)	,290
Schulabschluss (Образование)	,549
ALTER, BEFRAGTE<R>, KATEGORISIERT (Возраст, опрошенного(ой), разбит на категории)	-,520
Berufsausbildung (Профессиональное образование)	,164
(Constant) (Постоянно)	-1,297

Unstandardized coefficients (нестандартизированные коеффициенты)

Functions at Group Centroids (Функции для групповых центроидов)

INGL DIC	Function (Функция)
1
1 ,00 (Постматериалистический тип)	,380
2,00 (Материалистический тип)	-.374

Unstandardized canonical discriminant functions evaluated at group means (Нестандартизированные канонические дискриминантные функции, оценка которых происходит относительно средних значений групп).

В данном случае мы отказались от вывода очень длинной таблицы, в которой для каждого наблюдения построчно, приводится информация о значении дискриминантной функции и принадлежности к одной из двух групп.

В заключении приводится классификационная таблица с указанием точности попадания прогнозов:

Classification Resultsа

(Классификационные результаты)
	INGL_DIC (Индекс Инглехарта, дихото-мический)	Predicted Group Membership (Прогнозируемая принадлежность к группе)	Total (Сум-ма)
1,00 (Постматери-алисти-ческий тип)	2,00 (Материа-листи-ческий тип)
Original (Перво-начально)	Count (Коли-чество)	1 ,00 (Пост-материа-листи-ческий тип)	710	381	1091
2,00 (Материа-листический тип)	410	699	1109
Ungrouped cases (He сгруп-пирован-ные наблю-дения)	7	12	19
%	1 ,00 (Постматериа-листический тип)	65,1	34,9	100,0
2,00 (Материа-листи-ческий тип)	37,0	63,0	100,0
Ungrouped cases (He сгруп-пирован-ные наблю-дения)	36,8	63,2	100,0

а. 64,0% of original grouped cases correctly classified (64 % наблюдений, первоначально разнесённых по группам, были классифицированы корректно).

Правая колонка таблицы ("Total" (Сумма)) указывает на общее количество наблюдений, которые фактически относятся к соответствующим группам. К группе постматериалистических типов относится 1091 наблюдение, а к группе материалистических типов 1109. Обе колонки, объединенные общим наименованием ("Predicted Group Membership" (Прогнозируемая принадлежность к группе)), указывают на фактическое количество наблюдений, относящихся к каждой из групп. Первая колонка указывает на количество наблюдений, которые были отнесены к первой группе. Из 1091 постматериалистическйх наблюдений корректно определены были 710, это соответствует 65,1 % всех наблюдений. 381 наблюдение было по ошибке отнесено ко 2 группе, что соответствует 34,9 % всех наблюдений. Из 1109 материалистических наблюдений по ошибке к группе 1 были отнесены 410, что соответствует 37,0 %. 699 наблюдений были корректно отнесены к группе 2, что составило 63 %. Строка "Ungrouped cases" (Несгруппированные наблюдения) содержит наблюдения, которые не соответствуют ни одной из групп. Хотя эти наблюдения и не учитываются при расчёте дискриминантной функции, значение функции для них всё равно вычисляется. Из 19 наблюдений, для которых отсутствуют данные о принадлежности к какой-либо группе, 7 были отнесены к постматериалистическим типам, а 12 к материалистическим. В строке под таблицей приводится итоговый результат. 64 % наблюдений были классифицированы корректно. Так как даже при чисто случайном отнесении некоторого наблюдения к одной из двух имеющихся групп, корректность классификации данного наблюдения составила бы 50 %, то 64 %-ную точность прогноза следует рассматривать как довольно умеренный результат. Такой неудовлетворительный результат можно попытаться объяснить тем, что в обе группы входили смешанные типы, которые тяжелее классифицировать, нежели чистые типы. Проверим это предположение путём повторного проведения расчёта, но уже с учётом только чистых типов.

Выберите в меню Data (Данные) Select Cases... (Выбрать наблюдения)

Щёлкните на опции If condition is satisfied (Если выполняется условие) и затем на выключателе If... (Если).

В редакторе условий введите следующее условие:

ing1_ind = 1 OR ing1_ind = 4

Подтвердите нажатием Continue (Далее) и затем ОК.

В диалоговом окне Discriminant Analysis (Дискриминантный анализ) переменную ingl_ind (не ingl_dic!) поместите в поле для групповых переменных. В качестве границ области изменения задать значения 1 и 4.

В список независимых переменных поместите переменные statpaps, schule, alter и ausbild.

Дополнительные установки под выключателями Statistics... (Статистики), Classify... (Классифицировать) и Save... (Сохранить) произведите так, как было описано ранее.

Вы получите следующую классификационную таблицу:

Classification Results

(Результаты классификации)
	INGLEHART-INDEX (Индекс Инглехарта, дихото-мический)	Predicted Group Membership (Прогнозируемая принадлежность к группе	Total (Сумма)
POSTMATE-RIALISTEN (Постмате-риалисты)	MATERI-ALISTEN (Матери-алисты)
Original (Перво-начально)	Count (Коли-чество)	POSTMATE-RIALISTEN (Постмате-риалисты)	409	109	518
MATERI-ALISTEN (Матери-алисты)	133	297	430
%	POSTMATE-RIALISTEN (Постмате-риалисты)	79,0	21,0	100,0
MATERI-ALISTEN (Матери-алисты)	30,9	69,1	100,0

а. 74,5% of original grouped cases correctly classified (74,5 % наблюдений, первоначально разнесённых по группам, были классифицированы корректно).

К группе постматериалистов относится 518 наблюдений. 409 наблюдений (79 %) были спрогнозированы корректно, а 109 (21,0 %) по ошибке отнесены к группе 4 ("чистые материалисты"). В группе чистых материалистов насчитывается 403 наблюдения. 297 наблюдений (69,1 %) были определены корректно, а 133 (30,9 %) по ошибке были отнесены к группе 1 ("чистые постматериалисты"). Конечным результатом является корректная идентификация наблюдений, равная 74,5 %. Этот показатель значительно выше предыдущего и может быть расценен как приемлемый.

Диалоговое окно Discriminant Analysis: Statistics (Дискриминантный анализ: Статистики)

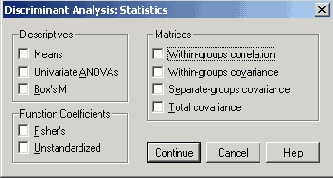
Активируйте опции: Means (Средние значения), Univariate ANOVAs (Одномерные тесты AN OVA), Unstandardized Func-tion Coefficients (He стандартизированные коэффициенты функции) и Within-groops Correlation Matrice (Корреляционная матрица внутри группы).

Подтвердите нажатием Continue (Далее).

Щёлкните на выключателе Classify... (Классифицировать). Откроется диалоговое окно Discriminant Analysis: Classification (Дискриминантный анализ: Классификация) (см. рис. 18.6).

Дискриминантный анализ

С помощью дискриминантного анализа на основании некоторых признаков (независимых переменных) индивидуум может быть причислен к одной из двух (или к одной из нескольких) заданных заранее групп.

Такая постановка задачи, в особенности в случае двух заранее заданных групп, очень сильно напоминает постановку задачи для метода логистической регрессии (см. гл. 16.4). Ядром дискриминантного анализа является построение так называемой дискриминантной функции

d = b1х1+b2х2+... + bnхn+а ,

где x1 и хn — значения переменных, соответствующих рассматриваемым случаям, константы b1-bn и a — коэффициенты, которые и предстоит оценить с помощью дискриминантного анализа. Целью является определение таких коэффициентов, чтобы по значениям дискриминантной функции можно было с максимальной четкостью провести разделение по группам.

Дискриминантный анализ

Глава 18. Дискриминантный анализ

Дискриминантный анализ 18.1 Пример из области медицины 18.2 Пример из области социологии 18.3 Пример из области биологии 18.4 Пример из области биологии (три группы)

Распределение значений дискриминантной функции для группы «скончался»

Распределение значений дискриминантной функции для группы «выжил»

Classification Results 3

(Классификационные результаты)
	Outcome (Исход)	Predicted Group Membership (Предсказанная принадлежность к одной из групп)	Total (Сум-ма)
gestorben (Сконча-лся)	ueberlebt (Выжил)
Original Перво-начально)	Count (Колич-ество)	gestorben (сконча-лся	38	25	63
ueberlebt (Выжил)	16	52	68
%	gestorben (сконча-лся	60,3	39,7	100,0
ueberlebt (Выжил)	23,5	76,5	100,0

а. 68,7% of original grouped cases correctly classified (68,7 % первоначально сгруппированных наблюдений были классифицированы корректно).

При применении метода логарифмической регрессии (см. гл. 16.4) результат получился немного лучше (доля корректного прогноза 70,99 %).

Для случая, когда пациенту мужского пола, 25 лет, ростом 184 см искусственное дыхание делали на протяжении 5 часов, при концентрации кислорода равной 0,7 и интенсивности соответствующей значению 10, получается следующее значение дискриминантной функции

d = 2,121 + 0,033*10 + 0,04*25 + 0,06*5 + 0,133*1-0,041*184 + 2,539*0,7 = -1,883

Опираясь на распределение значений дискриминантной функции, этого пациента можно отнести к группе выживших.

При выполнении дискриминантного анализа, как и для других многомерных процедур, можно применять и пошаговый образ действий, который как раз и рекомендуется при наличии большого количества независимых переменных. Этот метод похож на многомерный регрессионный анализ, однако переменные при проведении дискриминантного анализа выбираются по другим критериям.

Рассчитаем ещё раз наш пример, но уже с применением пошагового метода.

В исходном диалоговом окне дискриминантного анализа активируйте опцию Use stepwse method (Использовать пошаговый метод).

Щёлкните на кнопке Method... (Метод)

Откроется диалоговое окно Discriminant Analysis: Step-wise Method (Дискриминантаый анализ: Пошаговый метод).

Выберите метод, при помощи которого будет отобрана та переменная, которая увеличивает расстояние Махаланобиса (Mahalanobis) между двумя группами. Эта дистанционная мера базируется на евклидовых расстояниях между нормализованными значениями выборок с учётом корреляции соответствующих переменных.

Чтобы искусственно не раздувать объём выводимых результатов, в этот раз через кнопку Classify... (Классифицировать), активируйте опцию Summary table (Сводная таблица).

В рассматриваемом случае мы отказываемся от графического представления результатов. В анализ по очереди будут включены переменные: bzeit, gr, alter и kob; это те же самые переменные, которые использовались при применении метода логистической регрессии. По заключительной классификационной таблице можно сделать вывод о том, что в результате отбрасывания неподходящих переменных доля попаданий слегка выросла. Значение надежности прогноза составило 70,2 %.

Для проведения дискриминантного анализа Вы можете использовать и пример с двумя диагностическими тестами для обнаружения карциномы мочевого пузыря, рассмотренный в главе 16.4. Здесь можно получить более чёткое разделение двух групп (здоров — болен). Точность прогнозирования здесь составляет 82,2 %.