U-тест по методу Манна и Уитни
14.1.1 U-тест по методу Манна и Уитни
Это самый известный и самый распространенный тест непараметрического сравнения двух независимых выборок. Он основан на использовании одной общей последовательности значений обоих выборок.
Мы хотим проверить, отличаются ли показатели сахара в крови для мужчин и женщин в примере об исследовании гипертонии (файл hyper.sav).
Если Вы построите гистограмму показателя сахара в крови (переменная bz0), то заметите явную деформацию распределения в левую сторону. Тест Колмогорова-Смирнова (см. гл. 14.5) также показывает очень значительное отклонение от нормального распределения. Стало быть, для сравнения обоих выборок следует вместо t-теста Стьюдента применить U-тест по методу Манна и Уитни.
Откройте файл hyper.sav.
Выберите в меню Analyze (Анализ) Nonparametric Tests (Непараметрические тесты) 2 Independent Samples... (Две независимые выборки)
Появится диалоговое окно Two Independent Samples Tests (Тесты для двух независимых выборок) (см. рис. 14.1).
U-тест по методу Манна и Уитни является предварительной установкой.
Перенесите переменную bz0 из поля исходных переменных в поле тестируемых переменных, а переменную g в поле групповых переменных.
После щелчка на кнопке Define Groups (Определить группы). Вы получите возможность внести коды (1 — мужской и 2 — женский), необходимые для идентификации групп.
После щелчка на Continue Вы опять попадаете в исходное диалоговое окно.
Запустите программу вычисления путём нажатия на ОК.
В окне просмотра появятся следующие результаты:
Тест Мозеса (Moses)
14.1.2 Тест Мозеса (Moses)
Данный тест проверяет различие размаха двух независимых выборок, которые состоят из переменных, относящихся к порядковой шкале, причем одна выборка рассматривается как контрольная группа, а другая как экспериментальная. Так как размах экстремальных значений может давать искаженные представления, то при помощи установки по умолчанию по обеим сторонам распределения контрольной группы отсекаются в обшей сложности 5 процентов значений.
Однако, это может привести к тому, что реальные различия в наблюдаемых значениях переменных, будут искусственно стёрты. Это можно увидеть на следующем примере, который уже рассматривался при изучении U-теста по Манну и Уитни.
Откройте файл hyper.sav.
В диалоговом окне Two Independent Samples Tests (Тесты для двух независимых выборок) удалите флажок для U-теста по методу Манна и Уитни и отметьте вместо этого тест Мозеса (Moses extreme reactions).
В качестве тестовой переменной выберите переменную rrsl, а в качестве групповой переменной переменную med с кодировками 1 и 2.
Запустите программу вычисления путём нажатия на ОК. В окне просмотра появятся следующие результаты:
Частоты
|
Медикамент |
N | |
|
syst. Blutdruck, Ausgangswert (Систолическое давление, через 1 месяц) |
Alphasan (контрольный) |
87 |
|
Betasan (экспериментальный) |
87 | |
|
Total (Сумма) |
174 |
Статистика теста a,b
|
Систолическое давление, через 1 месяц | ||
|
Observed Control Group Span (Наблюдаемый размах контрольной группы) |
NSig. (1 -tailed) N Значимость (1 -сторонняя) |
167 ,032 |
|
Trimmed Control Group Span (Размах усеченной контрольной группы) |
N Sig. (1-tailed) N Значимость (1-сторонняя) |
156 ,500 |
|
Outliers Trimmed from each End (Выбросы удалены с обеих сторон) |
|
4 |
а. Тест Мозеса
b. Групповая переменная: медикамент
При проведении теста Мозеса первая из двух групп рассматривается как контрольная. Значения обеих групп располагаются на порядковой шкале и им присваиваются соответствующие ранговые места. В контрольной группе подсчитывается размах между этими ранговыми местами, то есть разность между большим и меньшим рангом. Этот размах равен 167 с соответствующим значением вероятности ошибки р = 0,032. Полученное значение вероятности ошибки указывает на значимое отклонение от размаха, ожидаемого при равномерном распределении. Эта значимость полностью исчезает (р = 0,500), если при подсчёте размаха контрольной группы удалить по четыре самых больших и самых малых ранга.
Тест Колмогорова-Смирнова
14.1.3 Тест Колмогорова-Смирнова
Условия применения данного теста такие же, как и при использовании U-теста по методу Манна и Уитни. Тест Колмогорова-Смирнова является предпочтительным тогда, когда количество категорий для тестируемых переменных ограничено. Если для такого j случая применять U-тест Манна и Уитни, то появляется большое количество ранговых мест, к которым относится сразу несколько переменных, то есть возникают неоднозначные ранговые последовательности. Основой теста является расчет максимальной разности между кумулятивными частотами обеих выборок. Эта разность обозначается величиной z, на основании которой, выводится вероятность ошибки р. В главе 11 рассматривался файл studium.sav, в котором при помощи переменной psyche отражалось психологическое состояние студентов (закодированное цифрами от 1 до 4 для значений: очень неустойчивое до очень устойчивое), а при помощи переменной sex — пол (1 = женский, 2 = мужской). Раньше различия между полами проверялись при помощи теста хи-квадрат. В данном случае для определения различия I можно также применить тест Колмогорова-Смирнова.
Откройте файл studium.sav.
Активируйте в диалоговом окне Two Independent Samples (Тесты для двух независимых выборок) тест Колмогорова-Смирнова.
Перенесите переменную psyche в поле тестируемых переменных, а переменной sex присвойте статус групповой переменной с категориями 1 и 2.
Запустите вычисления путём нажатия на ОК.
В окне просмотра появятся следующие результаты расчёта:
Статистика теста а
|
|
Psychische Lage | |
|
|
,370 ,000 -,370 | |
|
Most Extreme Differences (Самые экстремальные разности) |
Абсолютно Положительно Отрицательно | |
|
Z-Колмогорова-Смирнова |
| 1,875 |
| Asymp.Sig.(2-tailed) (Статистическая значимость (2-сторонняя) |
,002 | |
a. Grouping Variable: Geschlecht (Групповая переменная: пол)
Получается очень значимая разница между полами в отношении психологического состояния (р = 0,002).
Тест Уалда-Вольфовица (Wald-Wolfowitz)
14.1.4 Тест Уалда-Вольфовица (Wald-Wolfowitz)
Условия применения данного теста те же, что и при U-тесте по методу Манна и Уитни или при тесте Колмогорова-Смирнова. Значения обоих групп выстраиваются в единую последовательность по рангу. Затем производится подсчёт количества смен группового признака, с помощью которого можно найти количество непрерывных
последовательностей (количество смен плюс 1). Если появляются одинаковые значения (ранговые связки), то выводятся значения минимального и максимального числа возможных непрерывных последовательностей. Исходя из количества непрерывных последовательностей, можно найти вероятность ошибки р. Данный тест не пригоден для переменных с малым числом категорий, так как в этом случае очень сильно возрастает количество ранговых связок.
В качестве примера рассмотрим уже многократно использовавшийся пример со сравнением показателя кровяного давления.
Откройте файл hyper.sav.
В диалоговом окне Two Independent Samples (Тесты для двух независимых выборок) активируйте тест Уалда-Вольфовица.
Перенесите переменную rrsl в поле для тестируемых переменных, переменной med присвойте статус групповой переменной с категориями 1 и 2.
Запустите вычисления путём нажатия ОК. В окне просмотра появятся следующие результаты:
Статистика теста b,c
|
Number of Runs (Число непрерывных последователь- ностей) |
Z |
Asymp. Sig. (1-tailed) (Статисти- ческая значимость , (1 -сторонняя)) | ||
|
Syst. Blutdruck, nach 1 Monat (Систолическое давление, через 1 месяц) |
Minimum Possible (Минимально возможное) |
13" |
-11,404 |
,000 |
|
Maximum Possible (Максимально возможное) |
146 а |
8,819 |
1,000 | |
a. There are 10 inter-group ties involving 165 cases. (Между группами насчитывается 10 связок, которые охватывают 165 наблюдений.)
b. Wald-Wolfowitz Test (Тест по методу Уалда-Вольфовица)
с. Grouping Variable: Medikament (Групповая переменная: медикамент)
В результате мы получаем различие между минимальной и максимальной возможной непрерывной последовательностью (значение Z) и связанную с ним вероятность ошибки. Так как рассчитываемые значения Z располагаются по обоим краям стандартного нормального распределения, то выборка может содержать исходные данные, не пригодные для проведения этого теста. Поэтому тест Уальда-Вольфовица является не очень убедительным, в особенности при наличии ранговых связок.
Сравнение двух независимых выборок
14.1 Сравнение двух независимых выборок
В этом разделе описано четыре теста. Наиболее часто применяемым является U-тест Манна и Уитни, который поэтому и будет представлен в первую очередь.
Тест Уилкоксона (Wilcoxon)
14.2.1 Тест Уилкоксона (Wilcoxon)
Этот тест является традиционным непараметрическим тестом для сравнения двух зависимых выборок. Он основан на построении ранговой последовательности абсолютных разностей пар значений.
Мы уже установили (см. раздел 14.1), что для обоих медикаментов после 1 месяца приема наблюдается значительное понижение систолического кровяного давления. Теперь мы хотим проверить, является ли это изменение закономерным. Для простоты мы сначала должны быть рассмотрены все наблюдения подряд, то есть без разделения на группы по принимаемым медикаментам.
Переменные rrs0 и rrs1 (начальный уровень систолического давления и уровень через месяц после начала приема медикамента) представляют собой типичный пример связанных (зависимых) выборок.
Откройте файл hyper.sav.
Выберите в меню Analyze (Анализ) Nonparametric Tests... (Непараметрические тесты) 2 Related Samples... (Две связанные выборки)
Вы сможете убедиться в том, что предварительно по умолчанию установлен тест Уил-коксона (см. рис. 14.2)
Теперь в поле тестируемых переменных нужно выделить две необходимые переменные и эту пару перенести в поле для спаренных переменных. В нашем примере такими переменными являются rrsO и rrsl.
Запустите тест Уилкоксона на исполнение нажатием клавиши ОК. В окне просмотра появятся результаты расчёта:
Ranks (Ранги)
|
N |
Mean Rank (Средний ранг) |
Sum of Ranks (Ранговая сумма) | ||
|
syst. Blutdruck, nach 1 Monat - syst. Blutdruck, Ausgangswert (Систолическое кровяное давление, через 1 месяц -систолическое кровяное давление, исходная величина) |
Negative Ranks (Отрицательные ранги) |
144а |
77,81 |
11204,00 |
|
Positive Ranks (Положительные ранги) |
8Ь |
53,00 |
424,00 | |
|
Ties (Связи) |
22е |
|
| |
|
Total (Сумма) |
174 |
|
| |
a. syst Blutdruck, nach 1 Monat < syst. Blutdruck, Ausgangswert (Систолическое кровяное давление, через 1 месяц < систолическое кровяное давление, исходная величина)
b. syst. Blutdruck, nach 1 Monat > syst. Blutdruck, Ausgangswert (Систолическое кровяное давление, через 1 месяц > систолическое кровяное давление, исходная величина)
с. syst. Blutdruck, nach 1 Monat = syst. Blutdruck, Ausgangswert (Систолическое кровяное давление, через 1 месяц = систолическое кровяное давление, исходная величина)
Статистика теста b
|
syst. Blutdruck, nach 1 Monat - syst. Blutdruck, Ausgangswert (Систолическое кровяное давление, через 1 месяц -систолическое кровяное давление, исходная величина) | |
|
Z |
-9,970а |
|
Asymp. Sig. (2-tailed) (Статистическая значимость (2-сторонняя)) |
,000 |
a. Based on positive ranks (Основано на положительных рангах)
b. Wilcoxon test (Тест Вилоксона)
Результаты расчёта включают следующие данные:
Знаковый тест
14.2.2 Знаковый тест
Условия применения данного теста те же, что и для теста Уилкоксона, но в отличие от него здесь ведётся подсчёт только положительных и отрицательных разностей, что может оказаться полезным тогда, когда различия между выборками будут не слишком заметны.
До и после проведения курса лечения 67 пациентов были опрошены на предмет их самочувствия со следующими вариантами ответов: "хорошее", "относительно нормальное" или "плохое". Из 5 пациентов, самочувствие которых до прохождения курса лечения было хорошим, 3 после лечения отметили ответ "хорошее", а 2 "относительно нормальное". 18 пациентов до курса лечения оценили своё самочувствие как "относительно нормальное". 9 из них после лечения дали ответ "хорошее", 7 — "относительно нормальное" и 2 — "плохое". 44 пациента до лечения отозвались о своём самочувствии как о плохом. Из них 8 после лечения дали ответ "хорошее", 22 — "относительно нормальное", а 14 как и прежде — "плохое". Требуется проверить, является ли значимым успех лечения.
Данные находятся в файле kur.sav, который содержит переменные befl и bef2 (самочувствие до и после лечения с кодировками 1 = хорошо, 2 = относительно нормально, 3 = плохо) и n (частоты соответствующих комбинаций состояния пациентов).
Откройте файл kur.sav.
Используя меню Data (Данные) Weight cases... (Взвесить наблюдения) присвойте переменной п статус частотной переменной (см. гл. 8.7.2).
После вызова меню Analyze (Анализ) Nonparametric Tests (Непараметрические тесты) 2 Related Samples... (Две связанные выборки) откроется диалоговое окно Two-Related-Samples Tests (Тесты для двух связанных выборок).
Укажите переменные befl и bef2 в качестве тестируемой пары.
Из-за принятой кодировки переменных, вместо предварительно установленного теста Уилкоксона необходимо выбрать знаковый тест.
Запустите расчёт на исполнение при помощи нажатия ОК. В окне просмотра появятся следующие результаты расчёта:
Frequencies (Частоты)
|
|
N | |
|
Befinden nach der Kur - Befinden vor der Kur (Самочувствие после лечения - самочувствие до лечения) |
Negative Differences (Отрицательные разности) г |
39 |
|
Positive Differences (Положительные разности) " |
4 | |
|
Ties (Связки) с |
27 | |
|
Total (Сумма) |
67 | |
a. Befinden nach der Kur < Befinden vor der Kur (Самочувствие после лечения < самочувствие до лечения)
b. Befinden nach der Kur > Befinden vor der Kur (Самочувствие после лечения > самочувствие до лечения)
с. Befinden nach der Kur = Befinden vor der Kur (Самочувствие после лечения = самочувствие до лечения)
Test Statistics3 (Статистика теста)
|
Befinden nach der Kur - Befinden vor der Kur (Самочувствие после лечения - самочувствие до лечения) | |
|
Z |
-5,185 |
|
Asymp. Sig. (2-tailed) (Статистическая значимость (2-сторонняя)) |
,000 |
a. Sign test (Знаковый тест)
Результаты расчёта дают 39 отрицательных разностей (bef2 < befl), которые свидетельствуют о наступлении улучшений и 4 положительных разности, а в 24 наблюдениях изменений самочувствия не наблюдается. Вследствие того, что количества положительных и отрицательных разностей отличаются, значение z получается равным -5,185; этому показателю соответствует вероятность ошибки р < 0,001. Стало быть, наблюдается очень значимый успех лечения.
Тест хи-квадрат по методу МакНемара (McNemar)
14.2.3 Тест хи-квадрат по методу МакНемара (McNemar)
Данный тест применяется исключительно при наличии дихотомических переменных. При этом для двух зависимых переменных выясняется, происходят ли какие-либо изменения в структуре распределения их значений. В большинстве наблюдений сравнение проводится с учётом временного фактора по схеме "до — после".
В качестве примера рассмотрим исследование, проведенное в области стоматологии, где изучается факт кровоточивости дёсен до и после лечения.
Откройте файл zahnblut.sav.
Он содержит две переменные b1 и b2, которые своими кодировками (1 = да, 2 = нет) указывают на наличие кровоточивости дёсен соответственно до и после лечения.
В диалоговом окне Two-Related-Samples Tests (Тесты для двух связанных выборок) выберите тест МакНемара и перенесите обе переменные Ы и Ь2 в поле тестируемых пар.
Запустите расчёт на исполнение нажатием кнопки ОК. В окне просмотра появятся следующие результаты:
Zahnfleischbluten vor Behandlung & Zahnfleischbluten nach Behandlung (Кровоточивость дёсен до лечения & Кровоточивость дёсен после лечения)
|
Zahnfleischbluten vor Behandlung (Кровоточивость дёсен до лечения) |
Zahnfleischbluten nach Behandlung (Кровоточивость дёсен после лечения) | |
|
|
2 | 1 |
|
1 |
362 |
808 |
|
2 |
240 |
1565 |
Test Statistics (Статистика теста) b
|
Zahnfleischbluten vor Behandlung & Zahnfleischbluten nach Behandlung (Кровоточивость дёсен до лечения & Кровоточивость дёсен после лечения) | |
|
N |
2975 |
|
Chi-Square (Хи-квадрат) а |
306,764 |
|
Asymp. Sig. (Статистическая значимость) |
,000 |
a. Continuity Corrected (Непрерывность откорректирована) b. McNemar Test (Tea МакНемара)
Принимая во внимание кодировки выясняется, что в 808 наблюдениях после лечения кровоточивость дёсен исчезла, однако, с другой стороны, в 240 наблюдениях после прохождения курса лечения вновь появилась. В 362 наблюдениях кровоточивость оставалась постоянной. В 1565 наблюдениях кровоточивости не наблюдалось ни перед, ни после лечения. В соответствии с вероятностью ошибки, соответствующей величине критерия хи-квадрат (р < 0,001), можно констатировать, что разница между количеством улучшений (808) и количеством ухудшений (240) является очень значимой.
Сравнение двух зависимых выборок
14.2 Сравнение двух зависимых выборок
Понятие о зависимости выборок было рассмотрено в главе 5.1.3. Для проведения сравнения для таких выборок SPSS предлагает три различных теста, среди которых установленным по умолчанию является тест Уилкоксона. Заслуживает внимания так же и знаковый тест. При наличии дихотомических переменных применяется тест хи-квадрат по методу МакНемара.
Н-тест по методу Крускала и Уоллиса
14.3.1 Н-тест по методу Крускала и Уоллиса
Этот тест является модификацией U-теста Манна и Уитни на случай для более двух 1езависимых выборок. Он также базируется на общей ранговой последовательности значений всех выборок.
В данном случае нам необходимо протестировать четыре возрастные категории из рассмотренного выше исследования гипертонии на предмет значимости различия исходного показателя систолического кровяного давления.
Откройте файл hyper.sav Если бы Вы через меню Analyze (Анализ) Compare Means (Сравнить средние значения) Means... (Средние значения) вычислили средние значения исходного показателя давления (переменная rrs0) для четырёх возрастных категорий, то получили бы следующие результаты:
Report (Сводка)
jyst. Blutdruck, Ausgangswert (Систолическое кровяное давление, исходное значение)
|
Altersklassen (Возрастные категории) |
Mean (Среднее значение) |
N |
Std. Deviation (Стандартное отклонение) |
|
до 55 лет |
170,38 |
52 |
15,37 |
|
56-65 лет |
172,16 |
51 |
13,12 |
|
66-75 лет |
175,64 |
47 |
13,62 |
|
> 75 лет |
168,75 |
24 |
11,44 |
|
Сумма |
172,10 |
174 |
13,86 |
Для проверки значимости выберите в меню Analyze (Анализ) Nonparametric Tests (Непараметрические тесты) К Independent Samples... (Несколько независимых выборок)
Появится диалоговое окно Tests for Several Independent Samples (Тесты для нескольких независимых выборок) (см. рис. 14.3).
Н-тест по методу Крускала и Уоллиса является установкой по умолчанию.
Перенесите переменную rrs0 в поле тестируемых переменных, а переменную ak, которая описывает четыре возрастные категории, в список групповых переменных.
Медианный тест
14.3.2 Медианный тест
Для всех независимых выборок вычисляется общая медиана; затем подсчитывается, какое количество измеряемых величин находится ниже и выше медианы. Это приводит к построению полевой таблицы, содержащей 2*k полей, которая затем подвергается тесту хи-квадрат. Как уже указывалось, эффективность данного теста не очень высока.
Используем пример, использованный для изучения Н-теста по Крускалу и Уоллису.
В этот раз вместо указанного теста активируйте медианный тест.
Запустите расчёт путём нажатия ОК.
В окне просмотра появятся следующие результаты:
Frequencies (Частоты)
|
Altersklassen (Возрастные категории) | |||||
|
|
|
до 55 лет |
56-65 лет | 66-75лет | >75лет |
|
syst. Blutdruck, Ausgangswert (Систолическое кровяное давление, исходная величина) |
> медианы <= медианы |
18 |
19 | 24 |
7 |
|
34 |
32 | 23 |
17 | ||
Test Statistics (Статистика для теста) b
|
syst. Blutdruck, Ausgangswert (Систолическое кровяное давление, исходная величина) | |
|
N |
174 |
|
Медиана |
170,00 |
|
Хи-квадрат |
4,333а |
|
Df |
3 |
|
Asymp. Sig. (Статистическая значимость) |
,228 |
a. 0 cells (,0%) have expected frequencies less than 5. The minimum expected cell frequency is 9,4. (В 0 ячеек (,0%) ожидается значение частоты менее 5. Минимальная ожидаемая частота в ячейке равна 9,4.)
b Grouping Variable: Altersklassen (Групповая переменная: возрастные категории)
Так как в Н-тесте получилась р = 0,079, то он оказывается более подходящим для выявления закономерностей.
Сравнение более чем двух независимых выборок
14.3 Сравнение более чем двух независимых выборок
Наряду Н-тестом по Крускалу и Уоллису, который установлен по умолчанию, предлагается тест медиан, не очень рекомендуемый для применения.
Тест Фридмана
14.4.1 Тест Фридмана
Этот тест представляет собой расширение теста Уилкоксона для случая наличия более чем двух зависимых выборок. Он основывается на ранговых последовательностях, которые строятся для значений всех переменных участвующих в тесте.
Если Вы с помощью меню Analyze (Анализ) Reports (Сводка) Case Summaries... (Итоги по наблюдениям)
произведёте расчёт медиан для диастолического кровяного давления из исследования гипертонии (файл hyper.sav) для четырёх последовательных моментов времени (переменные rrdO, rrdl, rrd6, rrd!2), то получите следующие значения:
Case Processing Summary (Сводная таблица наблюдений)
|
Median (Медианы) | |||
|
diast. Blutdruck, Ausgangswert (Диастоли- ческое кровяное давление, исходная величина) |
diast. Blutdruck, nach 1 Monat (Диастолическое кровяное давление, через 1 месяц ) |
diast. Blutdruck, nach 6 Monaten (Диастоли- ческое кровяное давление, через 6 месяцев) |
diast. Blutdruck, nach 12 Monaten (Диастоли- ческое кровяное давление, через 12 месяцев) |
|
100,00 |
95,00 |
90,00 |
85,00 |
Видно, что Диастолическое кровяное давление непрерывно снижается. Этот факт следует проверить при помощи теста на значимость. В приведенном примере речь идёт о нескольких (а именно, — о четырёх) связанных выборках. Подходящим непараметрическим тестом для сравнения этих выборок является тест Фридмана.
Откройте файл hyper.sav.
Выберите в меню Analyze (Анализ) Nonparametric Tests (Непараметрические тесты) К Related Samples... (Две связанные выборки)
В диалоговом окне Вы увидите, что предварительно установлен тест Фридмана (см. рис. 14.4).
Перенесите по очереди переменные rrd0, rrdl, rrd6 и rrd12 в поле тестируемых переменных. После щелчка на кнопке Statistics... (Статистики) у Вас появилась бы возможность организовать вывод дескриптивных статистик и квантилей, но в данном случае мы от этого воздержимся.
Запустите расчёт путём нажатия ОК.
W Кендала
14.4.2 W Кендала
Коэффициент согласованности Кендала (W) измеряет степень согласованности между несколькими связанными выборками. Он был специально разработан для проведения тестов в ситуации, когда большое количество рецензентов высказывают своё мнение о большом количестве рецензируемых персон (объектов).
При этом рецензируемые образуют отдельные переменные, а рецензенты — отдельные наблюдения. На этом несколько неожиданном разделении следует остановиться подробнее. Каждый рецензент при помощи заданных наперед оценок выстраивает рецензируемых по рангу. Затем для каждого рецензируемого определяется сумма ранговых номеров. Исходя из этих сумм, определяется масштаб различных отзывов. Коэффициент согласованности W, вычисленный на основании этого масштаба, указывает на меру согласия между рецензентами. Коэффициент согласованности может принимать значения между 0 и 1. Значение 1 соответствует наличию полного согласия.
Три крупные спортивные газеты оценивали футболистов высшей лиги, игравших в прошлом туре чемпионата, при помощи оценок от 1 до 6 (к примеру 1 за "мировой уровень" и 6 за "не отработал свои деньги"). Оценки для 22 футболистов, участвовавших в одной игре, находятся в файле fussball.sav, который содержит три наблюдения, соответствующие трем рецензентам и 22 переменные (sl-s22), соответствующие 12 рецензируемым игрокам.
Откройте файл fussball.sav.
Переместите в диалоговом окне Tests for Several Related Samples (Тесты для нескольких связанных выборок) переменные sl-s22 в поле тестируемых переменных.
Вместо предварительно установленного теста Фридмана активируйте РК-тест Кендала.
Запустите расчёт путём нажатия ОК. В окне просмотра появятся следующие результаты:
Ranks (Ранги)
|
Mean Rank (Усреднённый ранг) | |
|
S1 |
12,33 |
|
S2 |
6,17 |
|
S3 |
10,33 |
|
S4 |
3,50 |
|
S5 |
8,50 |
|
S6 |
19,33 |
|
S7 |
18,50 |
|
S8 |
10,50 |
|
S9 |
6,17 |
|
S10 |
14,67 |
|
S11 |
16,67 |
|
S12 |
12,67 |
|
S13 |
6,67 |
|
S14 |
15,33 |
|
S15 |
19,67 |
|
S16 |
3,33 |
|
S17 |
12,33 |
|
S18 |
17,00 |
|
S19 |
2,17 |
|
S20 |
12,33 |
|
S21 |
16,33 |
|
S22 |
8,50 |
Test Statistics (Статистика теста)
|
N |
3 |
|
W Кендала а |
,741 |
|
Хи-квадрат |
46,695 |
|
Df |
21 |
|
Asymp. Sig. (Статистическая значимость) |
,001 |
a. Kendall's Coefficient of Concordance (Коэффициент согласованности Кендала)
Очень значимый (р = 0,001) коэффициент согласованности W (0,741) указывает на высокую согласованность всех трёх спортивных газет при оценке 22 игроков.
Q Кохрана
14.4.3 Q Кохрана
Этот тест представляет собой расширенный хи-квадрат-тест по МакНемару для случая с несколькими зависимыми выборками; стало быть, он может применяться при наличии более чем двух дихотомических переменных.
В главе 21 будет описан файл neugier.sav, который содержит 18 вопросов, с помощью которых исследовалась степень любопытства респондентов. Следующие три вопроса взяты из этого файла:
|
Вопрос 10: |
Хотели бы Вы полететь на Луну? |
|
Вопрос 12: |
Спрашивали ли Вы себя когда-нибудь, как будет выглядеть мир через сто лет? |
|
Вопрос 14: |
Предоставили бы Вы себя в руки учёных для проведения научных экспериментов? |
Переменные, соответствующие ответам на эти вопросы, имеют кодировки 1 (да) и 2 (нет). Мы должны найти ответ на вопрос, существуют ли значимые отличия в ответах на эти три вопроса.
Откройте файл neugier.sav.
В диалоговом окне Tests for Several Related Samples (Тесты для нескольких связанных выборок) переместите переменные item10, item12 и item14 в поле тестируемых переменных.
Вместо установленного теста Фридмана активируйте Q-тест Кохрана.
Запустите расчёт путём нажатия ОК. В окне просмотра появятся следующие результаты:
Frequencies (Частоты)
|
Value (Значение) | ||
|
2 | ||
|
item 10 |
9 |
21 |
|
item 12 |
15 |
15 |
|
item14 |
12 |
18 |
Test Statistics (Статистика теста)
|
N |
30 |
|
Q тест Кохрана |
3,375" |
|
df |
2 |
|
Asymp. Sig. (Статистическая значимость) |
,185 |
a. 2 is treated as a success. (2 рассматривается, как успешный результат).
К результатам данного теста относятся частоты для обеих категорий переменных и тестовое значение Q, полученное на основании распределения хи-квадрат. Между частотными распределениями ответов на эти вопросы не существует значимого различия (р = 0,185).
Сравнение более чем двух зависимых выборок
14.4 Сравнение более чем двух зависимых выборок
Наиболее часто применяемым является тест Фридмана, в то время как W-тест Кендала и Q-тест Кохрана предназначены для отдельных специальных случаев.
Тест Колмогорова-Смирнова для проверки формы распределения
14.5 Тест Колмогорова-Смирнова для проверки формы распределения
При помощи этого теста по выбору можно проверить, соответствует ли реальное распределение переменной нормальному, равномерному, экспоненциальному распределению или распределению Пуассона. Разумеется, самым распространённым видом проверки является проверка наличия нормального распределения.
Чтобы продемонстрировать работу данного теста, проверим на предмет наличия нормального распределения исходные значения холестерина, то есть переменную cho10 из файла hyper.sav.
Откройте файл hyper.sav.
Выберите в меню Analyze (Анализ) Nonparametric Tests (Непараметрические тесты) 1-Sample KS (К-С одной выборки)
Появится диалоговое окно One Sample .\olomgorov-Smirnov Test (Тест Колмогорова-Гмирнова для одной выборки) (см. рис. 4.5).
Перенесите переменную cho10 в поле тестируемых переменных.
Если Вы щёлкните на кнопке Options... (Опции), то сможете дополнительно организовать вывод характеристик дескриптивной статистики и квартилей.
Щёлкните на ОК.
Отдельный тест по критерию хи-квадрат
14.6 Отдельный тест по критерию хи-квадрат
С помощью этого теста проверяют, насколько значительно отличаются друг от друга наблюдаемые и ожидаемые частоты переменных, относящихся к номинальной шкале. Как правило, при этом ожидаемая частота подчиняется равномерному распределения; однако в SPSS существует возможность задать соответствующие пропорции.
Одним из примеров ожидаемого равномерного распределения частот являются кости. Предположим, Вы бросили один игральную кость 3000 раз и получили следующее частоты для выпавших очков.
|
Число очков |
Частота |
Число очков |
Частота |
|
1 |
511 |
4 |
498 |
|
2 |
472 |
5 |
513 |
|
3 |
572 |
6 |
434 |
Исходя из предположения об идеальности игральную кость (равной вероятности выпадения любого числа очков), ожидаемая частота для каждого из выпавших чисел составит 3000 / 6 = 500. Необходимо проверить, значимо ли отличаются наблюдаемые частоты от ожидаемых. Данные, а именно переменные augen (число очков) и n (частота), находятся в файле wuerfel.sav. Последнюю переменную следует применить в качестве весовой переменной.
Откройте файл wuerfel.sav.
Сначала выберите в меню Data (Данные) Weight Case (Взвесить наблюдения)
Переменную n объявите частотной (см. гл. 8.7), выберите в меню Analyze (Анализ) Nonparametric Tests (Непараметрические тесты) Chi-Square (Хи-квадрат) Откроется диалоговое окно Chi-Square Test (Тест хи-квадрат) (см. рис. 14.6).
Перенесите переменную augen в поле тестируемых переменных.
Если Вы, как в рассматриваемом примере, хотите подвергнуть анализу все категории тестируемых переменных, то оставьте в разделе Expected range (Ожидаемый диапазон) включённой опцию Get from Data (Из исходных данных); в противном случае у Вас есть возможность ограничить вовлекаемые категории посредством ввода нижней и верхней границ. Так как ожидаемые частоты одинаковы для всех категорий (была принята гипотеза о равномерном распределении), то эта предварительная установка остаётся в силе.
После нажатия кнопки Опции... у Вас появится возможность организовать вывод характеристик дескриптивной статистики и квартилей (что в данном случае является абсолютно бессмысленным).
Запустите расчёт путём нажатия ОК.
В окне просмотра появятся следующие результаты:
Augenzahl (Число очков)
|
Observed N (Наблюдаемое N) |
Expected N (Ожидаемое N) |
Residuals (остатки) | |
|
1 |
511 |
500,0 |
11,0 |
|
2 |
472 |
500,0 |
-28,0 |
|
3 |
572 |
500,0 |
72,0 |
|
4 |
498 |
500,0 |
-2,0 |
|
5 |
513 |
500,0 |
13,0 |
|
6 |
434 |
500,0 |
-66,0 |
|
Total (Сумма) |
3000 |
|
|
Test Statistics (Статистика теста)
|
Augenzahl (Число) | |
|
Chi-Square (Хи-квадрат) а |
21,236 |
|
Df |
5 |
|
Asymp. Sig. (Статистическая значимость) |
,001 |
a. 0 cells (,0%) have expected frequencies less than 5. The minimum expected cell frequency is 500,0. (В 0 ячеек (,0%) ожидаемая частота имеет значение менее 5. Минимальная ожидаемая частота в одной ячейке равна 500,0.)
Получилось очень значимое значение критерия хи-квадрат (р = 0,001). В рассматриваемом случае желателен вывод не абсолютных, а стандартизированных остатков, определяемых по формуле:
Биномиальный тест
14.7 Биномиальный тест
Этот тест проверяет дихотомические переменные на наличие различия между частотами обоих проявлений признака. Недихотомические переменные могут быть диэтомизированы (разделены на две категории) при помощи задания некоторой разделительной величины.
Представьте себе, что Вы играете со своим партнёром по теннису 50 матчей и выигрываете 29. Ваш партнёр, выигравший 21 раз, думает, что Вы ничем не лучше, а эта разница является случайной.
Чтобы это проверить можно выполнить биномиальный тест.
Откройте файл match.sav, содержащий две переменные: spieler и n.
Первая переменная имеет кодировки 1 и 2, которые соответствуют двум игрокам. Переменная n указывает на частоту выигрыша; ей присваивается статус весовой переменной.
Сначала выберите в меню Data (Данные) Weight Cases (Взвесить наблюдения)
Укажите переменную п как частотную переменную (см. гл. 8.7).
Затем выберите в меню Analyze (Анализ) Nonparametric Tests (Непараметрические тесты) Binomial (Биномиальное распределение)
Откроется диалоговое окно Binomial Test (Тест на биномиальное распределение) см. рис. 14. 7.
Перенесите щелчком переменную spieler в поле тестируемых переменных.
Если бы эта переменная не была дихотомической, Вы бы могли в поле Определить дихотомию (Define Dichotomy) ввести разделительную величину для проведения раздвоения (дихотомизации). Предварительно установленная тестовая пропорция (0,50) показывает на ожидаемую относительную частоту появления первой из двух дихотомических категорий. Здесь Вы можете задать и другое значение. После нажатия кнопки Options... (Опции) Вы можете организовать вывод (абсолютно бессмысленных) характеристик дескриптивной статистики.
Запустите расчёт путём нажатия ОК.
В окне просмотра появятся следующие результаты:
Binomial Test (Тест на биномиальное распределение)
|
Category (Категория) |
N |
Observed Prop. (Наблюда- емая пропорция) |
Test Prop. (Тестовая пропорция) |
Asymp. Sig. (2-tailed) (Статисти- ческая значимость (2-сторонняя)) | ||
|
SPIELER (Игрок) |
Группа 1 |
1 |
29 |
,58 |
,50 |
,322а |
|
Группа 2 |
2 |
21 |
,42 |
|
| |
|
Total (Сумма) |
|
50 |
1,00 |
|
| |
a. Based on Z Approximation. (Основываясь на Z-аппроксимации.)
Анализ последовательностей
14.8 Анализ последовательностей
При проверке последовательности дихотомических значений переменной выясняется следующий вопрос: идёт ли речь о случайном ряде или ряд построен в соответствии с определённой закономерностью.
В качестве примера рассмотрим три различные очереди людей, стоящих у кассы кинотеатра, учитывая пол.
1. Очередь: мжмжмжмжмжмжмжмжмжмж
2. Очередь: жмжммжжммжмжмжжмжммж
3. Очередь: мжжжжммммжжжжмжжмжмж
В первой очереди можно заметить явную закономерность, т.к. посетители стоят всегда по парам, при чём мужчина всегда стоит впереди. Во второй очереди, также просматривается попарный рисунок, хотя очерёдность мужчин и женщин меняется Третья очередь была выстроена генератором случайных чисел. Для первой очереди следует ожидать значительное отклонение от случайной последовательности, для второй очереди скорее всего так же, а для третьей нет.
Данные рассматриваемого примера соответствуют трем переменными rl, r2 и r3 в файле kino.sav. Мужчинам присвоен код 0, а женщинам 1.
Откройте файл kino.sav.
Выберите в меню Analyze (Анализ) Nonparametric Tests (Непараметрические тесты) Runs (Последовательности) Появится диалоговое окно Runs Test (Критерий серий) см. рис. 14.8.
Перенесите переменные rl, г2 и гЗ в поле тестируемых переменных.
Диалоговое окно One Sample Kolomgorov-Smirnov Test (Тест Колмогорова-Смирнова для одной выборки)
Диалоговое окно One Sample Kolomgorov-Smirnov Test (Тест Колмогорова-Смирнова для одной выборки)
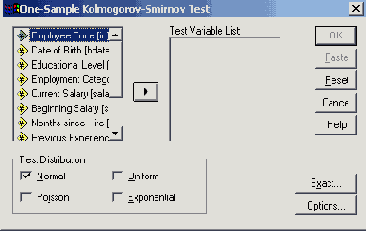
Предварительно установленной является проверка на нормальное распределение. В окне просмотра появятся следующие результаты:
One-Sample Kolmogorov-Smirnov Test (Тест Колмогорова-Смирнова для одной выборки)
|
Cholesterin, Ausgangswert (Холестерин, исходная величина) | ||
|
N |
|
174 |
|
Normal Parameters (Параметр нормального распределения) а' ь |
Mean (Среднее значение) Std. Deviation (Стандартное отклонение) |
237,27 49,42 |
|
Most Extreme Differences (Экстремальные разности) |
Absolute (Абсолютные) Positive (Положительные) Negative (Отрицательные) |
,057 ,057 -,046 |
|
Z Колмогорова-Смирнова |
|
,756 |
|
Asymp. Sig. (2-tailed) (Статистическая значимость (2-сторонняя)) |
|
,616 |
a. Test distribution is Normal. (Тестируемое распределение является нормальным распределением.)
b. Calculated from data. (Рассчитано исходя из исходных данных.)
Полученные результаты включают:
среднее значение и стандартное отклонение
промежуточные результаты, полученные в результате теста Колмогорова-Смирнова
вероятность ошибки р.
Отклонение от нормального распределения считается существенным при значении р < 0,05; в этом случае для соответствующих переменных следует применять непараметрические тесты. В рассматриваемом примере ( значение р = 0,616), то есть вероятность ошибки является не значимой; поэтому значения переменной достаточно хорошо подчиняются нормальному распределению.
Диалоговое окно Runs Test (Тест для последовательностей)
Диалоговое окно Runs Test (Тест для последовательностей)
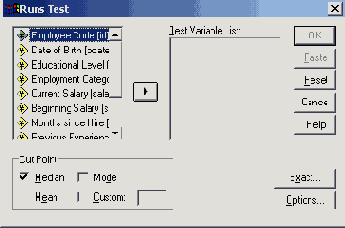
Для дихотомических переменных, закодированных при помощи 0 и 1, как в рассматриваемом примере, активируйте в поле Cut Point (Разделительная величина) опцию Custom (Пользовательская) и введите значение 1.
Запустите расчёт путём нажатия ОК.
В окне просмотра появятся следующие результаты.
Runs Test (Критерий серий)
|
Test Value (Проверяемое значение) " |
R1 1 |
R2 1 |
R3 1 |
|
Total Cases (Общее количество случаев) |
20 |
20 |
20 |
|
Number of Runs (Количество последовательностей) |
20 |
15 |
10 |
|
Z |
3,905 |
1,608 |
-,048 |
|
Asymp. Sig. (2-tailed) (Статистическая значимость (2-сторонняя)) |
,000 |
,108 |
,962 |
|
а. User-specified. (Определяется пользователем) | |||
Вычисленные программой значения р соответствуют ожиданиям.
Диалоговое окно СЫ-Square Test (Хи-квадрат-тест)
Диалоговое окно СЫ-Square Test (Хи-квадрат-тест)
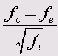
(см. гл. 11.1). При помощи основополагающего правила, приведенного в главе 8.7.2, можно точно определить те категории, для которых наблюдается значительное отклонение наблюдаемых частот от ожидаемых:
Стандартизированные остатки >= 2,0 указывают на значительное, >= 2,6 на очень значительное и >= 3,3 на сверх значительное отклонение. Если следовать этому правилу, то в экспериментах с игральной костью наблюдается очень значимое превышение количества выпадений 3 очков и очень, очень значимое занижение количества выпадений 6 очков.
Во втором примере, который принадлежит к области ботаники, нужно проверить не равномерное распределение, а наличие распределения подчиняющегося заданному соотношению.
Потомки трёх сортов бобовой культуры были разделены на три типа, которые находятся в соотношении между собой как 1:2:1. Во время некоторого эксперимента, проведенного с сотней таких потомков тип 1 появился 29 раз, тип 2 — 44 раза и тип 3 — 27 раз. Необходимо исследовать значительно ли отклоняется полученное распределение от теоретического распределения 1:2:1.
Данные находятся в файле bohnen.sav, причём переменная typ соответствует типу, а переменная n частоте.
Откройте файл bohnen.sav.
Сначала действуйте так же, как в первом примере, и взвесьте наблюдения с частотной переменной n.
В диалоговом окне Chi-Square Test (тест Хи-квадрат) присвойте переменной typ статус тестируемой переменной.
В поле Expected values (Ожидаемые значения) активируйте в этот раз опцию Values (Значения). Введите числа 1, 2 и 1 в предусмотренное для этого поле, и щёлкните дополнительно на кнопке Add (Добавить).
Запустите расчёт путём нажатия ОК. В окне просмотра появятся следующие результаты:
Тур (Тип)
|
Observed N (Наблюдаемое N) |
Expected N (Ожидаемое N ) |
Residual (Остаток) | |
|
1 |
29 |
25,0 |
4,0 |
|
2 |
44 |
50,0 |
-6,0 |
|
3 |
27 |
25,0 |
2,0 |
|
Total (Сумма) |
100 |
|
|
Test Statistics (Статистика теста)
|
Тур (Тип) | |
|
Chi-Square (Хи-квадрат) а |
1,520 |
|
Of |
2 |
|
Asymp. Sig. (Статистическая значимость) |
,468 |
а. 0 cells (,0%) have expected frequencies less than 5. The minimum expected cell frequency is 25,0. (В 0 ячеек (,0%) ожидаемая частота имеет значение менее 5. Минимальная ожидаемая частота в одной ячейке равна 25,0.)
Ожидаемые частоты выстроены в соответствии с заданным соотношением. На сей раз значимого отклонения наблюдаемых частот от ожидаемых не наблюдается (р = 0,468).
Диалоговое окно Тест на биномиальное распределение
Диалоговое окно Тест на биномиальное распределение
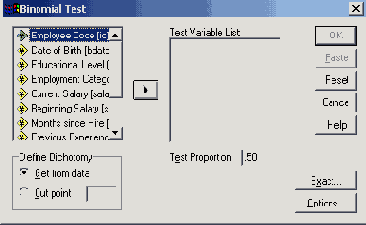
В выводимые результаты включают наблюдаемые абсолютные и относительные частоты обеих категорий, а так же ожидаемую относительную частоту первой категории Полученная вероятность ошибки (р = 0,322) говорит о том, что между наблюдаемой и ожидаемой относительными частотами не существует значимого различия. Стало быть и разница между обеими частотами выигрыша не является значимой.
Диалоговое окно Tests for Several Independent Samples (Тесты для нескольких независимых выборок)
Диалоговое окно Tests for Several Independent Samples (Тесты для нескольких независимых выборок)
Щёлкните на Define Range... (Определить диапазон) и введите значения 1 и 4 для минимального и максимального значения переменной соответственно.
Вернувшись снова в исходное диалоговое окно (щелчок на Далее), начните вычисления путём щелчка на ОК.
В окне просмотра появятся следующие результаты:
Ranks (Ранги)
|
Altersklassen (Возрастные категории) |
N |
Mean Rank (Средний ранг) | |
|
syst. Blutdruck, Ausgangswert (Систолическое давление, исходная величина) |
до 55 лет |
52 |
79,76 |
|
56-65 лет |
51 |
87,51 | |
|
66-75 лет |
47 |
102,17 | |
|
> 75 лет |
24 |
75,52 | |
|
Total (Сумма) |
174 |
|
Test Statistics (Статистика теста) а, b
|
syst. Blutdruck, Ausgangswert (Систолическое кровяное давление, исходная величина) | |
|
Chi-Square (Хи-квадрат) |
6,801 |
|
Df |
3 |
|
Asymp. Sig. (Статистическая значимость) |
,079 |
a. Kruskal Wallis Test (Тест Крускала-Уолхлиса)
b. Grouping Variable: Altersklassen (Групповая переменная: Возрастные категории)
В результаты расчёта входят:
усреднённые ранги в отдельных группах (где большим значениям отдаются более высокие места) и
величина критерия хи-квадрат, соответствующее число степеней свободы (df) и вероятность ошибки р.
В данном примере для которого р = 0,079 граница значимости преодолена незначительно, это означает, что всё же наблюдается тенденция к проявлению закономерности. В случае выявления существенной закономерности, для определения групп, которые значимо отличаются друг от друга, необходимо протестировать все группы попарно (как в тесте по методу Манна и Уитни).
Диалоговое окно Tests for Several Related Samples (Тесты для нескольких связанных выборок)
Диалоговое окно Tests for Several Related Samples (Тесты для нескольких связанных выборок)
В окне просмотра появятся следующие результаты:
Ranks (Ранговые ряды)
|
Mean Rank (Средний ранг) | |
|
diast. Blutdruck, Ausgangswert (Диастолическое кровяное давление, исходная величина ) |
3,81 |
|
diast. Blutdruck, nach 1 Monat Диастолическое кровяное давление, через 1 месяц ) |
2,57 |
|
diast. Blutdruck, nach 6 Monaten (Диастолическое кровяное давление, через 6 месяцев) |
2,02 |
|
diast. Blutdruck, nach 12 Monaten (Диастолическое кровяное давление, ЧЙПРЗ 1 9 Миля! ien^ |
1,60 |
Test Statistics (Статистика теста)a
|
N |
174 |
|
Chi-Square (Хи-квадрат) |
317,754 |
|
Df |
3 |
|
Asymp. Sig. (Статистическая значимость) |
,000 |
а. Тест Фридмана
Полученные результаты содержат:
усреднённые ранги участвующих переменных (где большим значениям присваиваются более высокие места) и
количество наблюдений, величина критерия хи-квадрат, полученная в результате теста, соответствующее число степеней свободы (df) и вероятность ошибки р.
В приведенном примере получился очень значимый показатель р < 0,001. Теперь, применяя попарное тестирование, при помощи теста Уилкоксона Вы самостоятельно можете выяснить, какие временные моменты по отдельности отличаются друг от друга.
Диалоговое окно Two-Related-Samples Tests (Тесты для двух связанных выборок)
Диалоговое окно Two-Related-Samples Tests (Тесты для двух связанных выборок)
количества, средние ранги и ранговые суммы для отрицательных и положительных разностей (причём большим абсолютным разностям присваивается более высокое ранговое место)
количество нулевых разностей и
контрольную величину z с соответствующей вероятностью ошибки р.
Полученная в приведенном примере величина р = 0,000 свидетельствует об очень значимой разнице.
Теперь повторим тест, но отдельно для каждого медикамента. Это значит, что один раз расчёт нужно произвести с условием med = 1, а второй с условием med = 2.
Для расчёта можно применить метод "Выбрать наблюдения", однако метод "Разделить файл" является более быстрым (см. гл. 7.4).
Выберите в меню Data (Данные) Split file... (Разделить файл)
Активируйте опцию Organize output by groups (Выводить результаты по группам), и перенесите переменную med в поле Groups based on (Группы основываются на).
Т.к. данные не сортированы по групповым признакам, оставьте опцию Sort the File by grouping variables... (Файл сортировать по групповым признакам) включённой и щёлкните на ОК.
Проведите ещё раз тест Уилкоксона, как было описано в начале раздела. Теперь он производится отдельно для каждого медикамента.
Диалоговое окно Two Independent Samples Tests (Тесты для двух независимых выборок)
Диалоговое окно Two Independent Samples Tests (Тесты для двух независимых выборок)

Ранги
|
|
Пол |
N |
Mean Rank (Усреднённый ранг) |
Sum of Ranks (Ранговая сумма) |
|
Blutzucker, Ausgangswert (Сахар, исходное значение) |
maennlich (Мужской) |
59 |
81,66 |
4818,00 |
|
weiblich Женский |
115 |
90,50 |
10407,00 | |
|
Total (Сумма) |
174 |
|
|
Статистика теста а
|
Blutzucker, Ausgangswert (Сахар, исходное значение) | |
|
Mann-Whitney U jU-тест по Манну и Уитни) |
3048,000 |
|
W Уилкоксона |
4818,000 |
|
Z |
-1,096 |
|
Asymp. Sig. (2-tailed) Асимптотическая значимость (2-сторонняя) |
,273 |
a Grouping Variable: Geschlecht (Групповая переменная: пол).
Выведенные результаты включают следующие показатели:
количество наблюдений, усреднённые ранги и ранговая сумма для двух выборок (причём большим значениям присваиваются низшие ранговые места),
тестовую величину U, определенную с помощью теста Манна и Уитни,
наименьшее значение из обоих ранговых сумм (W-тест Уилкоксона),
точное значение вероятности ошибки р при количестве наблюдений менее 30 и
тестовую величину z, определенную по тесту Колмогорова-Смирнова, а также относящуюся к ней вероятность ошибки р, которую следует использовать при количестве наблюдений более 30.
Выясняется, что в рассматриваемом примере разница показателей сахара в крови между полами не является статистически значимой (р = 0,273).
Нажав кнопку Options, Вы можете выбрать дополнительные возможности вывода данных, относящихся к рассмотренному и к другим непараметрическим тестам. Наряду с обычной обработкой пропущенных значений, можно организовать расчет дескриптивных статистик (среднее значение, минимум, максимум, стандартное отклонение, количество наблюдений) и квартилей (25, 50 и 75 процентили). Однако в этом случае характеристики дескриптивной статистики будут определяться одновременно для тестируемых и группирующих переменных. Это абсолютно бесполезно, так как в данном случае дескриптивная статистика имеет смысл только для тестируемых переменных, разбитых на группы по группирующим переменным. К сожалению, данная ошибка не была исправлена и в 10 версии SPSS.
В рассмотренном примере проведения U-теста был бы также очень полезен расчет медиан обеих групп. Медианы определяются с помощью других средств SPSS. В нашем примере медиана показателя сахара для мужчин равна 93, а для женщин 97.
Непараметрические тесты
Глава 14. Непараметрические тесты
Непараметрические тесты 14.1 Сравнение двух независимых выборок 14.1.1 U-тест по методу Манна и Уитни 14.1.2 Тест Мозеса (Moses) 14.1.3 Тест Колмогорова-Смирнова 14.1.4 Тест Уалда-Вольфовица (Wald-Wolfowitz) 14.2 Сравнение двух зависимых выборок 14.2.1 Тест Уилкоксона (Wilcoxon) 14.2.2 Знаковый тест 14.2.3 Тест хи-квадрат по методу МакНемара (McNemar) 14.3 Сравнение более чем двух независимых выборок 14.3.1 Н-тест по методу Крускала и Уоллиса 14.3.2 Медианный тест 14.4 Сравнение более чем двух зависимых выборок 14.4.1 Тест Фридмана 14.4.2 W Кендала 14.4.3 ОКохрана 14.5 Тест Колмогорова-Смирнова для проверки формы распределения 14.6 Отдельный тест по критерию хи-квадрат 14.7 Биномиальный тест 14.8 Анализ последовательностейНепараметрические тесты
Непараметрические тесты
Непараметрические (не основанные на каком-либо распределении вероятности) тесты применяются там, где выборки из переменных, принадлежащих к интервальной шкале, не подчиняются нормальному распределению. Так как в этих тестах обрабатывается не само измеренное значение, а его ранг (положение внутри выборки), то эти тесты нечувствительны к выбросам. Непараметрические тесты применяются также в тех случаях, когда переменные относятся к порядковой, а не к интервальной шкале. В меню Analyze (Анализ) Nonparametric Tests (Непараметрические тесты)
SPSS предоставляет в распоряжение пользователей немалое количество непараметрических тестов. Все эти тесты приведены в нижеследующей таблице. В левой колонке находятся описания вспомогательных меню, а правая содержит описания тестов, вызываемых через соответствующие диалоговые окна.
|
Вспомогательные меню |
Аналоговое окно |
|
Chi-Square (Хи-квадрат) |
|
|
Binomial (Биномиальный) |
|
|
Runs (Последовательности) |
|
|
1 -Sample K-S... (Колмогоров-Смирнов для одной выборки) |
|
|
2 Independent Samples (Две независимые выборки) |
Mann-Withney-U-Test (U-тест Манна-Уитни) Moses extreme reactions (Экстремальные реакции по Мозесу) |
|
|
Z Kolomgorov-Smirnov (Z-тест Колмогорова-Смирнова |
|
|
Wald-Wolfowitz runs (Последовательности Уалда-Вольфовица) |
|
К Independent Samples (К независимых выборок) |
Н Kruskal-Wallis (Н-тест Крускала-Уоллиса) Median (Медианный тест) |
|
2 Related Samples (Две связанные выборки) |
Wilcoxon (Тест Уилкоксона) Sign (Знак) |
|
|
McNemar (Тест МакНемара) |
|
К Related Samples (К связанных выборок) |
Friedman (Тест Фридмана) |
|
|
W Kendall (W-тест Кендала) |
|
|
Q Cochran (Q-тест Кохрана) |
Наиболее часто применяемыми тестами являются тесты для сравнения двух и более независимых или зависимых выборок. Наиболее известными тестами, служащими для этих целей являются U-тест Манна-Уитни, Н-тест Крускала-Уоллиса, тест Уилкоксона и тест Фридмана. Важную роль также играет тест Колмогорова-Смирнова для одной выборки, который может применяться для проверки наличия нормального распределения.
Непараметрические тесты могут, конечно, применяться и в случае нормального распределения значений. Но в этом случае они будут иметь лишь 95 %-ую эффективность по сравнению с параметрическими тестами. Если Вы хотите, к примеру, произвести множественное сравнение средних значений двух независимых выборок, причем выборки являются частично подчиняются нормальному распределению, а частично — нет, то рекомендуется всегда применять U-тест Манна и Уитни.
