Обнаружение ошибок ввода
10.1 Обнаружение ошибок ввода
Самый точный метод проверки данных (то есть значений всех переменных) на ошибки при вводе состоит в том, чтобы командами меню Analyze (Анализ) Reports (Отчеты) Case summaries... (Сводка наблюдений) вывести их список (см. раздел 4.6) и сравнить каждое значение с оригиналом (например, анкетой). Однако этот способ требует очень много времени, особенно при большом объеме данных. Поэтому решиться на проведение такой скучной и утомительной работы можно только в редких случаях — как правило, когда объем данных ограничен. В общем случае рекомендуется проводить частотный анализ значений переменных; для этого служат команды меню Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Frequencies... (Частоты) (см. главу 6). Результаты этого анализа при внимательном рассмотрении позволяют выявить недопустимые значения. Например, если переменная содержит данные роста в сантиметрах, то значение 384, обнаруживаемое при частотном анализе, явно свидетельствует о том, что в данных имеется ошибка. После проведения частотного анализа это значение можно отыскать в файле данных и исправить. Следовательно, при изучении частотных таблиц особое внимание надо обращать на максимальное и минимальное значения. Однако если вместо возраста 65 лет было введено, например, значение 56, то при помощи частотной таблицы эту ошибку обнаружить невозможно. Часто имеется также возможность провести смысловой анализ данных путем создания таблиц сопряженности (см. главу 11). Например, если данные взяты из анкеты, в которой имелся вопрос о семейном положении (холост/не замужем, женат/замужем, вдовец/вдова, разведен(а)), то, построив таблицу сопряженности для этого вопроса и вопроса типа: «Если у вас есть семья, то приемлемо ли для вас проводить отпуск раздельно?», легко можно обнаружить, ответили ли на него только женатые/замужние опрашиваемые.
Обладая некоторыми практическими навыками и фантазией, с помощью описанных и им подобных способов можно выявить большое количество ошибок ввода. Все такие ошибки обязательно должны быть исправлены. Даже если наблюдений несколько тысяч, то даже одно-единственное противоречивое значение наносит вред вашему исследованию: создается впечатление, что работа по сбору о подготовке информации выполнена поверхностно.
Проверка закона распределения
10.2 Проверка закона распределения
В первую очередь представляет интерес закон распределения, особенно для переменных, относящихся к интервальной шкале и шкале отношений. Чаще всего при этом ставится вопрос, подчиняются ли значения переменных нормальному распределению. Именно от этого практически всегда зависит выбор соответствующих аналитических тестов.
В этом отношении самым распространенным и рекомендуемым является графическое изображение распределения данных в форме гистограммы (см. главы 6 и 22). Объективная проверка на нормальное распределение проводится с помощью подходящего статистического критерия (теста Колмогорова-Смирнова). Эта операция представлена в разделе 14.5.
Вычисление характеристик
10.3 Вычисление характеристик
SPSS предоставляет различные возможности для вычисления статистических характеристик, помогающих оценить положение вершины и разброс распределения. К таким характерам относятся, например, среднее значение, медиана, стандартное отклонение и т.д. Эти возможности перечислены в обзоре в начале главы 9.
В рамках исследования данных можно определить другие характеристики, называемые робастными оценками. Этот метод исследования данных также предоставляет возможности для обнаружения ошибок ввода (например, путем выявления выбросов) и проверки формы распределения.
Анализ без группирующей переменной
10.4.1 Анализ без группирующей переменной
Проведем анализ возраста пациентов.
Перенесите переменную а в список зависимых переменных (Dependent List). Так как сначала мы хотим выяснить, какие методы анализа выполняются по умолчанию, то не будем пока вносить никаких изменений в настройки.
Запустите вычисление, щелкнув на кнопке ОК. Будут созданы следующие таблицы:
Case Processing Summary (Обработанные наблюдения)
|
|
Cases (Случаи) | ||||
|
Valid (Допустимые) |
Missing (Отсутствующие) |
Total (Всего) | |||
|
N |
Percent |
N Percent |
N |
Percent | |
|
Возраст |
174 |
100,0% |
0 ,0% |
174 |
100,0% |
Descriptives (Описательная статистика)
|
|
Statistic |
Std. Error | ||
|
Возраст |
Mean (Среднее) |
|
62,11 |
,88 |
|
95% Confidence Interval for Mean (95% доверительный интервал среднего) |
Lower Bound (Нижняя граница) Upper Bound (Верхняя граница) |
|
60,38 63,84 | |
|
5% Trimmed Mean (5% усеченное среднее) |
|
62,25 |
| |
|
Median (Медиана) |
|
63,00 |
| |
|
Variance (Дисперсия) |
|
133,358 |
| |
|
Std. Deviation (Стандартное отклонение) |
|
11,55 |
| |
|
Minimum (Минимум) |
|
36 |
| |
|
Maximum (Максимум) |
|
87 |
| |
|
Range (Размах) |
|
51 |
| |
|
Interquartile Range (Межквартильная широта) |
|
17,25 |
| |
|
Skewness (Асимметрия) |
|
-,143 |
,184 | |
|
Kurtosis (Коэффициент вариации) |
|
-,635 |
,366 | |
Возраст Stem-and-Leaf Plot (диаграмма ветвей и листьев)
|
Frequency |
Stem & |
Leaf |
|
6,00 |
3 . |
677999 |
|
7,00 |
4 . |
0223333 |
|
14,00 |
4 . |
66677788888999 |
|
23,00 |
5 . |
01111111122223333333444 |
|
20,00 |
5 . |
55667777778888888899 |
|
27,00 |
6 . |
000011111222333333333444444 |
|
27,00 |
6 . |
555555666666677888888999999 |
|
24,00 |
7 . |
000000011111122233333444 |
|
13,00 |
7 . |
5566666788899 |
|
11,00 |
8 . |
00001111224 |
|
2,00 |
8 . |
67 |
|
Stem width : |
10 |
|
|
Each leaf: |
|
1 case(s) |
В этом случае окно вывода результатов содержит:
статистические характеристики,
диаграмму stem-and-leaf (ветвей и листьев)
коробчатую диаграмму (box plot).
Большую часть статистических характеристик мы уже рассмотрели в главах 6 и 9. Появились новые характеристики:
5% усеченное среднее: среднее значение, вычисленное без учета 5% наименьших и 5% наибольших значений.
95% доверительный интервал: доверительный интервал, в котором находится среднее значение с вероятностью 95%.
Межквартилъная широта: расстояние между первым и третьим квартилями.
Диаграмма ветвей и листьев представляет собой комбинацию гистограммы и табличного списка. Как на гистограмме, длина каждой строки соответствует количеству наблюдений, попадающих в определенный интервал. Но, сверх этого, на данной диаграмме выводится также наблюдаемое численное значение для каждого наблюдения. Для этой цели численное значения разбиваются на два компонента: ветвь, представляющую собой первую цифру или группу цифр и лист — последующие цифры. Ветвь соответствует тем разрядам численного значения наблюдаемой переменной, которые не изменяются, а листья — разрядам, которые изменяются в пределах избранного интервала. В рассматриваемом примере ветви разбиты на две части — одну для листьев с 0 по 4 и другую — для листьев с 5 по 9.
Коробчатая диаграмма состоит из прямоугольника, занимающего пространство от первого до третьего квартиля (то есть, от 25 до 75 процентиля). Линия внутри этого прямоугольника соответствует медиане. Кроме того, на коробчатой диаграмме отмечаются максимальное и минимальное значения, если только они не являются выбросами (см. ниже).
Значения, удаленные от границ более чем на три длины построенного прямоугольника (экстремальные значения), помечаются на диаграмме звездочками. Значения, удаленные более чем на полторы длины прямоугольника, помечаются кружками.
Теперь посмотрим, какие еще статистические характеристики можно вычислить в дополнение к стандартным.
Анализ для групп наблюдений
10.4.2 Анализ для групп наблюдений
Проанализируем исходное содержание холестерина (переменная cho10), которое содержится в файле hyper.sav, для четырех возрастных классов (переменная ak).
В диалоговом окне Explore кнопкой Reset (Сброс) восстановите настройки по умолчанию и перенесите переменную cholO в список зависимых переменных (Dependent List), а переменную ak — в список факторов (Factor List).
Щелкните на кнопке ОК.
В результате будут вычислены характеристики описательной статистики и построена диаграмма ветвей и листьев раздельно по четырем возрастным классам. На коробчатой диаграмме соответственно появятся четыре прямоугольника (см. рис. 10.8).
Остальные статистические параметры также можно вычислить раздельно по разным значениям группирующей переменной (в данном случае по возрастным классам). Это относится и к выводу гистограмм и диаграмм нормального распределения в окне просмотра.
Далее можно проверить, значимо ли различаются группы наблюдений, образованные в соответствии со списком факторов, по дисперсиям зависимых переменных. В нашем примере можно выяснить, существуют ли значимые различия между пациентами четырех возрастных классов по разбросу содержания холестерина. Такая проверка гомогенности дисперсий необходима, например, если требуется провести для четырех возрастных группах простой дисперсионный анализ на сравнение средних (см. главу 13). Дисперсионный анализ как раз предусматривает гомогенность распределения дисперсий по отдельным ячейкам.
В диалоговом окне Explore: Plots в группе Spread vs. Level with Levene Test (Зависимость «Разброс — средний уровень по тесту Левена») выберите опцию Power estimation (Экспоненциальная оценка).
Запустите вычисления, щелкнув на Continue и ОК.
Исследование данных
10.4 Исследование данных
Чтобы понять, что может предложить нам SPSS для решения этой задачи, возьмем для примера переменную а (Возраст) из исследования эффективности лекарств (см. главу 9).
Загрузите файл hyper.sav.
Перейдите к исследованию данных, выбрав команды меню Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Explore... (Исследовать) Откроется диалоговое окно Explore.
Диаграмма нормального распределения
Диаграмма нормального распределения

На диаграмме с исключенным трендом отклонения наблюдаемых значений от ожидаемых при нормальном распределении представлены в зависимости от наблюдаемых значений. В случае нормального распределения все точки лежат на горизонтальной прямой, проходящей через нуль. Явное отклонение от прямой указывает на отличие распределения от нормального. На этой диаграмме все значения, также подвергаются стандартизации (z-преобразованию) (см. рис. 10.7).
Диаграмма с исключенным трендом
Диаграмма с исключенным трендом

Заканчивая рассмотрение диалога Explore... (Исследовать), следует упомянуть еще кнопку Options... (Параметры), которая позволяет задать способ обработки пропущенных значений, и содержит группу опций Display (Показывать). Последняя позволяет запретить вывод диаграмм или статистических таблиц.
Диалоговое окно Explore: Plots
Диалоговое окно Explore: Plots

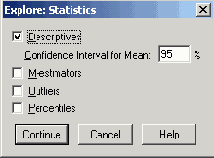
Диалоговое окно Explore: Statistics
Диалоговое окно Explore: Statistics
M-Estimators
|
|
Huber's M-Estimator ia) (М-оценка Губера) |
Tukey's Biweight (b) (Оценка Тьюки) |
Hampel M-Estimator (с) (М-оценка Хампеля) |
Andrews' Wave (d) (Волна Эндрюса) |
|
Возраст |
62,38 |
62,51 |
62,31 |
62,51 |
a. The weighting constant is 1,339 (Весовая константа равна 1,339).
b. The weighting constant is 4,685 (Весовая константа равна 4,685).
с. The weighting constants are 1,700, 3,400 and 8,500 (Весовые константы равны 1,700, 3,400 и 8,500).
d. The weighting constant is 1,340*pi (Весовая константа равна 1,340*pi).
Percentiles
|
|
Percentiles | ||||||
|
|
5 |
10 |
25 |
50 |
75 |
90 | 95 |
|
Weighted Возраст Average(Definition 1 ) (Взвешенное среднее, определение 1 ) |
42,00 |
47,00 |
53,00 |
63,00 |
70,25 |
78,00 |
81,00 |
|
Tukey's Hinges Возраст (угловые точки Тьюки) |
|
|
53,00 |
63,00 |
70,00 |
|
|
Extreme Values (Экстремальные значения)
|
|
Case Number (Номер случая) |
Value (Значение) | ||
|
Возраст |
Highest (Наибольшие значения) |
1 |
96 |
87 |
|
2 |
53 |
86 | ||
|
3 |
99 |
84 | ||
|
4 |
86 |
82 | ||
|
5 |
62 |
82 | ||
|
Lowest (Наименьшие значения) |
1 |
68 |
36 | |
|
2 |
23 |
37 | ||
|
3 |
64 |
37 | ||
|
4 |
122 |
39 | ||
|
5 |
45 |
.а | ||
a. Only a partial list of cases with the value 39 are shown in the table of lower extremes (В таблице наименьших экстремальных значений показан только частичный список наблюдений со значением 39).
В этих таблицах выводятся М-оценки Губера, Тьюки, Хампеля и волна Эндрюса. Основная идея М-оценок состоит в том, чтобы перед вычислением среднего значения присвоить отдельным наблюдениям разные веса. В распространенных М-оценках применяются веса, уменьшающиеся с удалением от центра распределения. Следовательно, обычное среднее значение можно рассматривать как М-оценку с единичными весами для всех наблюдений.
Из возможных процентилей выводятся семь значений: для 5, 10, 25, 50, 75, 90 и 95 процентов. Дополнительно вычисляются угловые точки Тьюки: 25%, 50% и 75%-про-центили.
В таблице «Экстремальные значения» выводятся пять наибольших и пять наименьших значений (выбросы).
Теперь обратимся к диаграммам, которые можно построить при исследовании данных в SPSS.
В диалоговом окне Explore щелкните на кнопке Plots... (Диаграммы). Откроется диалоговое окно Explore: Plots (см. рис. 10.4).
С коробчатой диаграммой и диаграммой ветвей и листьев мы уже ознакомились.
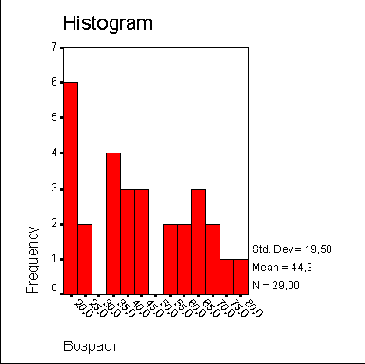
Поэтому в поле Boxplots (Коробчатые диаграммы) выберите опцию None (Нет) и снимите флажок Stem-and-leaf; вместо него установите флажок Histogram (Гистограмма).
Щелкните на кнопке Continue, а затем на ОК. В окне просмотра появится гистограмма.
Гистограмма возрастной структуры
Гистограмма возрастной структуры
Далее мы посмотрим, какие результаты можно получить, если установить в диалоговом окне Explore: Plots флажок Normality plots with tests (Диаграмма нормального распределения с тестами).
Установите этот флажок и подтвердите настройку кнопкой ОК.
В окне просмотра будет показан результат теста Лиллифора (модификации теста Колмогорова-Смирнова) на нормальное распределение.
Если в результате получена вероятность ошибки р менее 0,05, то данное распределение значимо отличается от нормального. В данном примере при р = 0,200 распределение можно считать нормальным. При объеме выборки менее 50 наблюдений проводится также тест Шапиро-Уилкса.
Tests of Normality (Тесты на нормальное распределение)
|
|
Kolmoqorov-Smirnov (а) (Колмогоров-Смирнов) | ||
|
Statistic |
df |
Sig. | |
|
Возраст |
,059 |
174 |
,200* |
*. This is a lower bound of the true significance (Это нижняя граница истинной значимости), a. Lilliefors Significance Correction (Коррекция значимости по Лиллифору).
В окне просмотра будут показаны две диаграммы:
диаграмма нормального распределения
диаграмма с исключенным трендом
По диаграмме нормального распределения (также называемой диаграммой Q-Q) можно визуально определить, достаточно ли близко заданное распределение приближается к нормальному. Здесь каждое наблюдаемое значение сравнивается со значением, ожидаемым при нормальном распределении. При условии точного выполнения нормального распределения все точки лежат на прямой. Наблюдаемые значения откладываются по оси X, а ожидаемые — по оси Y, при этом все значения подвергаются стандартизации (z-преобразованию). В данном примере (см. рис. 10.6) наблюдаемые значения достаточно близки к прямой.
Исследование данных
Глава 10. Исследование данных
Исследование данных 10.1 Обнаружение ошибок ввода 10.2 Проверка закона распределения 10.3 Вычисление характеристик 10.4 Исследование данных 10.4.1 Анализ без группирующей переменной 10.4.2 Анализ для групп наблюденийИсследование данных
Исследование данных
Когда данные введены в компьютер, не следует сразу же приступать к анализу. На первом этапе сами данные следует подвергнуть подробному и всестороннему исследованию. Подобное исследование преследует три основных цели:
Обнаружение ошибок ввода,
Проверка закона распределения,
Описание данных подходящими статистическими характеристиками.
Коробчатая диаграмма
Коробчатая диаграмма

В диалоговом окне Explore щелкните на кнопке Statistics... (Статистика).
Откроется диалоговое окно Explore: Statistics (см. рис. 10.3).
Статистические характеристики, установленные по умолчанию уже вычислены, поэтому флажок для них (Descriptives) можно снять.
Установите флажки для вычисления М-оценок Губера, Тьюки, Эндрюса и Хампеля (М-estimators), выбросов (Outliers) и процентилей (Percentiles).
Закройте диалог, щелкнув на Continue, и запустите вычисления кнопкой ОК. Результат этих вычислений приводится ниже.
Коробчатая диаграмма по группам
Коробчатая диаграмма по группам
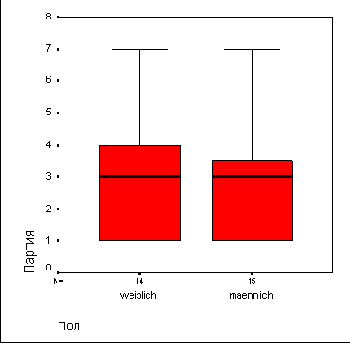
В результате во всех четырех вариантах будет проведен тест Левена на гомогенность дисперсий. Этот тест определяет уровень значимости (допустимую вероятность ошибки р. При р > 0,05 различие дисперсии между данными группами не значимо. Следовательно, их можно рассматривать как гомогенные. В данном примере тест Левена не дает значимого результата.
Test of Homogenity of Variances (Тест на гомогенность дисперсий)
|
|
Levene Statistic (Статистика Левена) |
df1 |
df2 |
Sig. (Значи-мость) | |
|
холестерин, исходный |
Based on Mean (На основе среднего) |
,190 |
3 |
170 |
,903 |
|
Based on Median (На основе медианы) |
,157 |
3 |
170 |
,925 | |
|
Based on Median and with adjusted df (Ha основе медианы и с уточненным df) |
,157 |
3 |
169,024 |
,925 | |
|
Based on trimmed mean (На основе усеченного среднего) |
,178 |
3 |
170 |
,912 | |
Далее выводится диаграмма, на которой для каждой группы изображена зависимость разброса значений от центрального значения. Точнее говоря, на оси X откладывается логарифм медианы, а на оси Y — логарифм межквартильной широты. Если дисперсии не гомогенны, а гетерогенны (тест Левена дает значимый результат, SPSS дает возможность провести так называемое степенное преобразование данных. Для этого выберите в диалоговом окне Explore: Plots опцию Transformed (С пре-5разованием) и в списке Power (Степень) выберите подходящую степень. Возможные степеные преобразования показаны в нижеследующей таблице.
|
Степень |
Преобразование |
|
3 |
кубическое |
|
2 |
квадратное |
|
| |
квадратный корень |
|
В |
натуральный логарифм. |
|
-1/2 |
величина, обратная квадратному корню |
|
-1 |
обратная величина |
Успешность преобразования можно оценить, вновь построив зависимость разброса от среднего уровня (Spread vs. Level with Levene Test). Однако с такими преобразованиями следует обходиться очень осторожно. Нелинейные преобразования изменяют отношения между группами, и, кроме того, статистические суждения в таком случае основываются уже не на исходных, а на преобразованных значениях.
Диалоговое окно Explore
Рис. 10.1: Диалоговое окно Explore
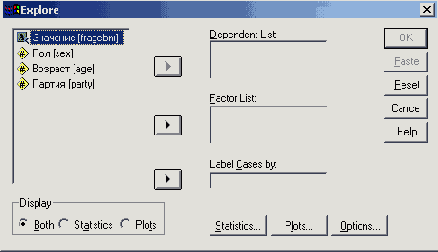
Поначалу вас может смутить то, что в этом диалоговом окне проводится различие между зависимыми переменными и факторами. Это означает, что можно выполнять анализ раздельно по группам наблюдений. В этом случае анализируемой переменной будет зависимая переменная, а группирующей переменной — фактор. Если же такой раздельный анализ проводить не требуется, список факторов не используется.
В следующем разделе мы рассмотрим для начала такой анализ данных, который не должен производиться по группам раздельно.
